A First Course in Probability Chap1-2 중간고사 범위

A-First-Course-in-Probability

Chapter

Combinatorial Analysis

1

1.1 서론 1.2 세기의 기본 원리 1.3 순열 1.4 조합 1.5 다항 계수 1.6 방정식의 정수해 개수

1.1 Introduction

다음은 확률과 관련된 일반적인 문제이다: 통신 시스템은 겉보기에 동일한 $n$ 개의 안테나를 선형으로 배열하여 구성된다. 이 시스템은 두 개의 연속된 안테나가 모두 불량인 경우가 없는 한 모든 수신 신호를 받을 수 있으며, 이 경우 **기능적(functional)**이라고 불린다. 만약 $n$ 개의 안테나 중 정확히 $m$ 개가 불량으로 판명된다면, 결과 시스템이 기능적일 확률은 얼마인가? 예를 들어, $n=4$ , $m=2$ 인 특별한 경우, 6가지 가능한 시스템 구성이 있다:

0	1	1	0
0	1	0	1
1	0	1	0
0	0	1	1
1	0	0	1
1	1	0	0

여기서 1은 안테나가 작동 중임을 의미하고 0은 불량임을 의미한다. 결과 시스템은 처음 3가지 배열에서는 기능적이고 나머지 3가지 배열에서는 기능적이지 않으므로, 원하는 확률을 $\frac{3}{6}=\frac{1}{2}$ 로 간주하는 것이 합리적이다. 일반적인 $n$ 과 $m$ 의 경우, 우리는 유사한 방식으로 시스템이 기능적일 확률을 계산할 수 있다. 즉, 시스템이 기능적이 되는 구성의 수를 세고, 이를 가능한 모든 구성의 총수로 나누는 것이다.

앞선 논의에서, 우리는 사건이 발생할 수 있는 방법의 수를 세는 효과적인 방법이 유용할 것이라는 것을 알 수 있다. 사실, 확률 이론의 많은 문제들은 특정 사건이 발생할 수 있는 다른 방법의 수를 세는 것만으로도 해결될 수 있다. **수학적 계수 이론(mathematical theory of counting)**은 공식적으로 **조합론(combinatorial analysis)**으로 알려져 있다.

1.2 The Basic Principle of Counting

**기본적인 셈의 원리(basic principle of counting)**는 우리의 모든 작업에 있어 근본적인 토대가 될 것이다. 느슨하게 말하면, 이 원리는 한 실험이 $m$ 가지 가능한 결과 중 하나를 낳을 수 있고, 다른 실험이 $n$ 가지 가능한 결과 중 하나를 낳을 수 있다면, 두 실험의 가능한 결과는 총 $mn$ 가지가 된다는 것을 의미한다.

The basic principle of counting

두 가지 실험이 수행된다고 가정해 보자. 실험 1이 $m$ 가지 가능한 결과 중 하나를 가질 수 있고, 실험 1의 각 결과에 대해 실험 2가 $n$ 가지 가능한 결과를 가질 수 있다면, 두 실험을 합쳐서 총 $mn$ 가지 가능한 결과가 존재한다.

기본 원리 증명: 기본 원리는 두 실험의 모든 가능한 결과를 열거함으로써 증명될 수 있다. 즉,

\begin{aligned} & (1,1),(1,2), \ldots,(1, n) \\ & (2,1),(2,2), \ldots,(2, n) \\ & \cdot \\ & \cdot \\ & (m, 1),(m, 2), \ldots,(m, n) \end{aligned}

여기서 실험 1이 $i$ 번째 가능한 결과를 낳고, 이어서 실험 2가 $j$ 번째 가능한 결과를 낳을 때, 그 결과를 $(i, j)$ 라고 한다. 따라서 가능한 결과들의 집합은 $m$ 개의 행으로 구성되며, 각 행은 $n$ 개의 원소를 포함한다. 이것이 결과를 증명한다.

Example 2a

10명의 여성으로 구성된 작은 공동체가 있으며, 각 여성은 3명의 자녀를 두고 있다. 만약 한 여성과 그녀의 자녀 중 한 명이 올해의 어머니와 자녀로 선정된다면, 몇 가지 다른 선택이 가능할까? 풀이 여성을 선택하는 것을 첫 번째 실험의 결과로, 그리고 그 여성의 자녀 중 한 명을 선택하는 것을 두 번째 실험의 결과로 간주하면, 기본 원리에 따라 $10 \times 3=30$ 가지의 가능한 선택이 있음을 알 수 있다.

수행해야 할 실험이 두 가지 이상일 때, 기본 원리는 일반화될 수 있다.

The generalized basic principle of counting

$r$ 개의 실험이 수행될 예정이며, 첫 번째 실험에서 $n_1$ 가지 가능한 결과가 나올 수 있고, 이 $n_1$ 가지 가능한 결과 각각에 대해 두 번째 실험에서 $n_2$ 가지 가능한 결과가 나올 수 있으며, 처음 두 실험의 가능한 결과 각각에 대해 세 번째 실험에서 $n_3$ 가지 가능한 결과가 나올 수 있다면, $\ldots$ , $r$ 개의 실험에서 총 $n_1 \cdot n_2 \cdots n_r$ 가지 가능한 결과가 나온다.

대학 기획 위원회는 신입생 3명, 2학년 4명, 3학년 5명, 4학년 2명으로 구성된다. 각 학년에서 1명씩 총 4명으로 구성된 소위원회를 선출해야 한다. 몇 개의 다른 소위원회가 가능한가?

풀이 소위원회 선택은 각 학년에서 한 명의 대표를 선택하는 네 가지 개별 실험의 결합된 결과로 볼 수 있다. 그러면 기본 원리의 일반화된 버전에 따라 $3 \times 4 \times 5 \times 2 = 120$ 가지 가능한 소위원회가 존재한다. $\square$

예제 2c

예제 2d

예제 2e

첫 3자리는 문자로, 마지막 4자리는 숫자로 구성되는 7자리 차량 번호판은 몇 개나 가능한가?

풀이 기본 원리의 일반화된 버전에 따라 답은 $26 \cdot 26 \cdot 26 \cdot 10 \cdot 10 \cdot 10 \cdot 10 = 175,760,000$ 이다. $\square$

$n$ 개의 점에 대해 정의된 함수 중 각 함수값이 0 또는 1인 함수는 몇 개나 가능한가?

풀이 점들을 $1, 2, \ldots, n$ 이라고 하자. 각 $i=1, 2, \ldots, n$ 에 대해 $f(i)$ 는 0 또는 1이어야 하므로, $2^n$ 가지 가능한 함수가 존재한다. $\square$

예제 2c에서 문자 또는 숫자 간의 반복이 금지된다면 몇 개의 번호판이 가능할까?

풀이 이 경우, $26 \cdot 25 \cdot 24 \cdot 10 \cdot 9 \cdot 8 \cdot 7 = 78,624,000$ 가지 가능한 번호판이 존재한다. $\square$

1.3 Permutations

문자 $a, b, c$ 로 만들 수 있는 서로 다른 순서 배열은 몇 가지가 있을까? 직접 열거해보면 $abc, acb, bac, bca, cab, cba$ 의 6가지가 있음을 알 수 있다. 각 배열은 **순열(permutation)**이라고 알려져 있다. 따라서 3개의 객체로 이루어진 집합의 가능한 순열은 6가지이다. 이 결과는 기본 원리(basic principle)를 통해서도 얻을 수 있는데, 순열의 첫 번째 객체는 3개 중 아무거나 될 수 있고, 두 번째 객체는 남은 2개 중 아무거나 선택할 수 있으며, 세 번째 객체는 남은 1개가 되기 때문이다. 따라서 $3 \cdot 2 \cdot 1 = 6$ 가지의 가능한 순열이 있다.

이제 $n$ 개의 객체가 있다고 가정해보자. 방금 3개의 문자에 대해 사용한 것과 유사한 추론을 적용하면, $n$ 개의 객체에 대한 서로 다른 순열의 수는 다음과 같음을 알 수 있다.

n(n-1)(n-2) \cdots 3 \cdot 2 \cdot 1=n!

$n!$ ("n 팩토리얼"이라고 읽음)은 $n$ 이 양의 정수일 때 $1 \cdot 2 \cdot \dots \cdot n$ 과 같도록 정의되지만, $0!$ 을 1로 정의하는 것이 편리하다.

Example 3a

예제 3b

9명의 선수로 구성된 야구팀에서 가능한 타순은 몇 가지인가?

풀이 가능한 타순은 $9!=362,880$ 가지이다. $\square$

확률 이론 수업은 남자 6명과 여자 4명으로 구성된다. 시험이 실시되고, 학생들은 성적에 따라 순위가 매겨진다. 두 학생이 같은 점수를 얻지 않는다고 가정한다. (a) 가능한 다른 순위는 몇 가지인가? (b) 남자들은 남자들끼리만, 여자들은 여자들끼리만 순위가 매겨진다면, 가능한 다른 순위는 몇 가지인가?

풀이 (a) 각 순위는 10명의 사람을 특정 순서로 배열하는 것에 해당하므로, 이 부분의 답은 $10!=3,628,800$ 이다. (b) 남자들끼리 가능한 순위는 $6!$ 가지이고, 여자들끼리 가능한 순위는 $4!$ 가지이므로, 기본 원리에 따라 이 경우 가능한 순위는 $(6!)(4!)=(720)(24)=17,280$ 가지이다.

예제 3c

예제 3d

존스 씨는 책장에 꽂을 책 10권을 가지고 있다. 이 중 4권은 수학책, 3권은 화학책, 2권은 역사책, 1권은 언어책이다. 존스 씨는 같은 과목의 책들이 모두 함께 책장에 있도록 책을 배열하고 싶어 한다. 가능한 다른 배열은 몇 가지인가?

풀이 수학책이 먼저, 그 다음 화학책, 그 다음 역사책, 그 다음 언어책 순서로 배열되는 경우는 $4!3!2!1!$ 가지이다. 마찬가지로, 과목들의 가능한 각 순서에 대해 $4!3!2!1!$ 가지의 배열이 가능하다. 따라서 과목들의 가능한 순서가 $4!$ 가지이므로, 원하는 답은 $4!4!3!2!1!=6912$ 이다.

이제 특정 객체들이 서로 구별할 수 없을 때 $n$ 개의 객체 집합의 순열의 수를 결정할 것이다. 이 상황을 명확히 이해하기 위해 다음 예제를 고려해 보자.

글자 $P E P P E R$ 로 만들 수 있는 다른 글자 배열은 몇 가지인가? 풀이 먼저, 3개의 $P$ 와 2개의 $E$ 가 서로 구별될 때, 글자 $P_{1} E_{1} P_{2} P_{3} E_{2} R$ 의 순열은 $6!$ 가지이다. 그러나 이러한 순열 중 하나를 고려해 보자. 예를 들어, $P_{1} P_{2} E_{1} P_{3} E_{2} R$ 이다. 이제 $P$ 들을 서로 순열하고 $E$ 들을 서로 순열하면, 결과적인 배열은 여전히 $PPEPER$ 형태일 것이다. 즉, 모든 $3!2!$ 순열은

\begin{array}{ll} P_{1} P_{2} E_{1} P_{3} E_{2} R & P_{1} P_{2} E_{2} P_{3} E_{1} R \\ P_{1} P_{3} E_{1} P_{2} E_{2} R & P_{1} P_{3} E_{2} P_{2} E_{1} R \\ P_{2} P_{1} E_{1} P_{3} E_{2} R & P_{2} P_{1} E_{2} P_{3} E_{1} R \\ P_{2} P_{3} E_{1} P_{1} E_{2} R & P_{2} P_{3} E_{2} P_{1} E_{1} R \\ P_{3} P_{1} E_{1} P_{2} E_{2} R & P_{3} P_{1} E_{2} P_{2} E_{1} R \\ P_{3} P_{2} E_{1} P_{1} E_{2} R & P_{3} P_{2} E_{2} P_{1} E_{1} R \end{array}

$PPEPER$ 형태이다. 따라서 글자 PEPPER의 가능한 글자 배열은 $6!/(3!2!)=60$ 가지이다.

일반적으로, 예제 3d에서 사용된 것과 동일한 추론은 다음과 같은 사실을 보여준다.

\frac{n!}{n_{1}!n_{2}!\cdots n_{r}!}

$n$ 개의 객체 중 $n_{1}$ 개가 동일하고, $n_{2}$ 개가 동일하고, $\ldots, n_{r}$ 개가 동일할 때, 가능한 다른 순열의 수는 위와 같다.

예제 3e

체스 토너먼트에는 10명의 경쟁자가 있으며, 이 중 4명은 러시아인, 3명은 미국인, 2명은 영국인, 1명은 브라질인이다. 토너먼트 결과가 선수들의 국적을 순위대로 나열한다면, 가능한 결과는 몇 가지인가?

풀이 가능한 결과는

\frac{10!}{4!3!2!1!}=12,600

가지이다.

Example 3f

9개의 깃발을 일렬로 걸어 만들 수 있는 서로 다른 신호의 개수는, 4개의 흰색 깃발, 3개의 빨간색 깃발, 2개의 파란색 깃발로 구성된 세트에서 만들 수 있으며, 같은 색의 깃발은 모두 동일하다고 가정한다.

풀이: 서로 다른 신호의 개수는 다음과 같다.

\frac{9!}{4!3!2!}=1260

$\square$

1.4 Combinations

우리는 종종 총 $n$ 개의 객체에서 $r$ 개의 객체로 구성될 수 있는 서로 다른 그룹의 수를 결정하는 데 관심을 갖는다. 예를 들어, $A, B, C, D, E$ 의 5개 항목에서 3개로 구성된 서로 다른 그룹은 몇 개를 선택할 수 있을까? 이 질문에 답하기 위해 다음과 같이 추론한다:

첫 번째 항목을 선택하는 방법은 5가지, 다음 항목을 선택하는 방법은 4가지, 마지막 항목을 선택하는 방법은 3가지이므로, 항목이 선택되는 순서가 관련될 때 3개 그룹을 선택하는 방법은 $5 \cdot 4 \cdot 3$ 가지이다. 그러나 3개로 구성된 모든 그룹(예를 들어, 항목 $A, B, C$ 로 구성된 그룹)은 6번(즉, 선택 순서가 관련될 때 모든 순열 $A B C, A C B, B A C, B C A, C A B, C B A$ 가 계산될 것이다) 계산될 것이므로, 형성될 수 있는 총 그룹의 수는 다음과 같다:

\frac{5 \cdot 4 \cdot 3}{3 \cdot 2 \cdot 1}=10

일반적으로, $n(n-1) \cdots(n-r+1)$ 은 선택 순서가 관련될 때 $n$ 개의 항목에서 $r$ 개의 항목으로 구성된 그룹을 선택할 수 있는 서로 다른 방법의 수를 나타내며, 각 $r$ 개 항목 그룹은 이 계산에서 $r!$ 번 계산될 것이므로, $n$ 개의 항목 집합에서 형성될 수 있는 서로 다른 $r$ 개 항목 그룹의 수는 다음과 같다:

\frac{n(n-1) \cdots(n-r+1)}{r!}=\frac{n!}{(n-r)!r!}

Notation and terminology

우리는 $r \leq n$ 일 때 $\binom{n}{r}$ 을 다음과 같이 정의한다.

\binom{n}{r}=\frac{n!}{(n-r)!r!}

그리고 $\binom{n}{r}$ ("n choose r"로 읽음)은 $n$ 개의 객체에서 $r$ 개를 선택하는 가능한 조합의 수를 나타낸다고 말한다.

따라서 $\binom{n}{r}$ 은 선택 순서가 중요하지 않을 때 $n$ 개의 객체 집합에서 선택할 수 있는 크기 $r$ 의 서로 다른 그룹의 수를 나타낸다.

동등하게, $\binom{n}{r}$ 은 크기 $n$ 의 집합에서 선택할 수 있는 크기 $r$ 의 부분집합의 수이다. $0!=1$ 을 사용하면 $\binom{n}{n}=\binom{n}{0}=\frac{n!}{0!n!}=1$ 임을 알 수 있는데, 이는 이전 해석과 일치한다. 왜냐하면 크기 $n$ 의 집합에는 크기 $n$ 의 부분집합이 정확히 1개(즉, 전체 집합) 있고, 크기 0의 부분집합이 정확히 1개(즉, 공집합) 있기 때문이다. 유용한 관례는 $r>n$ 이거나 $r<0$ 일 때 $\binom{n}{r}$ 을 0으로 정의하는 것이다.

예시 4a

20명으로 구성된 그룹에서 3명의 위원회를 구성해야 한다. 몇 개의 다른 위원회가 가능한가? 해답 가능한 위원회는 $\binom{20}{3}=\frac{20 \cdot 19 \cdot 18}{3 \cdot 2 \cdot 1}=1140$ 개이다.

예시 4b

5명의 여성과 7명의 남성으로 구성된 그룹에서 2명의 여성과 3명의 남성으로 이루어진 몇 개의 다른 위원회를 구성할 수 있는가? 만약 남성 중 2명이 불화가 있어 함께 위원회에서 일하기를 거부한다면 어떻게 되는가? 해답 2명의 여성을 선택하는 가능한 그룹은 $\binom{5}{2}$ 개이고, 3명의 남성을 선택하는 가능한 그룹은 $\binom{7}{3}$ 개이므로, 기본 원리에 따라 2명의 여성과 3명의 남성으로 구성된 가능한 위원회는 $\binom{5}{2}\binom{7}{3}= \left(\frac{5 \cdot 4}{2 \cdot 1}\right) \frac{7 \cdot 6 \cdot 5}{3 \cdot 2 \cdot 1}=350$ 개이다.

이제 남성 중 2명이 함께 일하기를 거부한다고 가정해 보자. 3명의 남성으로 구성된 가능한 그룹 $\binom{7}{3}=35$ 개 중 $\binom{2}{2}\binom{5}{1}=5$ 개는 불화가 있는 두 남성을 모두 포함하므로, 불화가 있는 두 남성을 모두 포함하지 않는 그룹은 $35-5=30$ 개이다. 2명의 여성을 선택하는 방법은 여전히 $\binom{5}{2}=10$ 가지이므로, 이 경우 가능한 위원회는 $30 \cdot 10=300$ 개이다.

예시 4c

$n$ 개의 안테나 중 $m$ 개가 불량이고 $n-m$ 개가 정상이라고 가정하고, 모든 불량 안테나와 모든 정상 안테나는 구별할 수 없다고 가정하자. 두 불량 안테나가 연속되지 않는 선형 배열은 몇 가지가 있는가? 해답 $n-m$ 개의 정상 안테나가 일렬로 배열되어 있다고 상상해 보자. 이제 두 불량 안테나가 연속되지 않으려면, 정상 안테나 사이의 각 공간에는 최대 하나의 불량 안테나만 포함되어야 한다. 즉, 그림 1.1에서 꺾쇠표시로 나타낸 $n-m$ 개의 정상 안테나 사이의 $n-m+1$ 개의 가능한 위치 중에서, 불량 안테나를 배치할 $m$ 개의 위치를 선택해야 한다. 따라서 두 불량 안테나 사이에 적어도 하나의 정상 안테나가 있는 가능한 배열은 $\binom{n-m+1}{m}$ 가지이다.

\begin{gathered} \wedge 1 \wedge 1 \wedge 1 \ldots \wedge 1 \wedge 1 \wedge \\ 1=\text { functional } \\ \wedge=\text { place for at most one defective } \end{gathered}

Figure 1.1 연속된 불량 안테나가 없는 경우.

유용한 조합론적 항등식은 다음과 같다.

\binom{n}{r}=\binom{n-1}{r-1}+\binom{n-1}{r} \quad 1 \leq r \leq n

식 (4.1)은 해석적으로 또는 다음 조합론적 논증을 통해 증명될 수 있다: $n$ 개의 객체 그룹을 고려하고, 이 객체들 중 특정 하나에 주목하여 이를 객체 1이라고 부르자. 이제 객체 1을 포함하는 크기 $r$ 의 그룹은 $\binom{n-1}{r-1}$ 개이다 (각각의 그러한 그룹은 나머지 $n-1$ 개의 객체에서 $r-1$ 개를 선택하여 형성되기 때문이다). 또한, 객체 1을 포함하지 않는 크기 $r$ 의 그룹은 $\binom{n-1}{r}$ 개이다. 크기 $r$ 의 그룹은 총 $\binom{n}{r}$ 개이므로, 식 (4.1)이 성립한다.

$\binom{n}{r}$ 값은 이항 정리에서 그 중요성 때문에 종종 **이항 계수(binomial coefficients)**라고 불린다.

The binomial theorem

(x+y)^{n}=\sum_{k=0}^{n}\binom{n}{k} x^{k} y^{n-k}

우리는 이항정리에 대한 두 가지 증명을 제시할 것이다. 첫 번째는 수학적 귀납법을 이용한 증명이고, 두 번째는 조합론적 고려사항에 기반한 증명이다.

귀납법을 이용한 이항정리 증명: $n=1$ 일 때, 식 (4.2)는 다음과 같이 간략화된다.

x+y=\binom{1}{0} x^{0} y^{1}+\binom{1}{1} x^{1} y^{0}=y+x

$n-1$ 에 대해 식 (4.2)가 성립한다고 가정하자. 이제,

\begin{aligned} (x+y)^{n} & =(x+y)(x+y)^{n-1} \\ & =(x+y) \sum_{k=0}^{n-1}\binom{n-1}{k} x^{k} y^{n-1-k} \\ & =\sum_{k=0}^{n-1}\binom{n-1}{k} x^{k+1} y^{n-1-k}+\sum_{k=0}^{n-1}\binom{n-1}{k} x^{k} y^{n-k} \end{aligned}

첫 번째 합에서 $i=k+1$ 로, 두 번째 합에서 $i=k$ 로 두면, 다음과 같이 정리할 수 있다.

\begin{aligned} (x+y)^{n} & =\sum_{i=1}^{n}\binom{n-1}{i-1} x^{i} y^{n-i}+\sum_{i=0}^{n-1}\binom{n-1}{i} x^{i} y^{n-i} \\ & =x^{n}+\sum_{i=1}^{n-1}\left[\binom{n-1}{i-1}+\binom{n-1}{i}\right] x^{i} y^{n-i}+y^{n} \\ & =x^{n}+\sum_{i=1}^{n-1}\binom{n}{i} x^{i} y^{n-i}+y^{n} \\ & =\sum_{i=0}^{n}\binom{n}{i} x^{i} y^{n-i} \end{aligned}

여기서 마지막에서 두 번째 등식은 식 (4.1)에 따른 것이다. 귀납법에 의해 이 정리는 이제 증명되었다.

이항정리의 조합론적 증명: 다음 곱을 고려해보자.

\left(x_{1}+y_{1}\right)\left(x_{2}+y_{2}\right) \cdots\left(x_{n}+y_{n}\right)

이것의 전개는 $2^{n}$ 개의 항의 합으로 구성되며, 각 항은 $n$ 개의 인수의 곱이다. 또한, 합에 있는 $2^{n}$ 개의 항 각각은 각 $i=1,2, \ldots, n$ 에 대해 $x_{i}$ 또는 $y_{i}$ 를 인수로 포함할 것이다. 예를 들어,

\left(x_{1}+y_{1}\right)\left(x_{2}+y_{2}\right)=x_{1} x_{2}+x_{1} y_{2}+y_{1} x_{2}+y_{1} y_{2}

이제, 합에 있는 $2^{n}$ 개의 항 중에서 $k$ 개의 $x_{i}$ 와 $(n-k)$ 개의 $y_{i}$ 를 인수로 갖는 항은 몇 개일까? $k$ 개의 $x_{i}$ 와 $(n-k)$ 개의 $y_{i}$ 로 구성된 각 항은 $n$ 개의 값 $x_{1}, x_{2}, \ldots, x_{n}$ 중에서 $k$ 개의 그룹을 선택하는 것에 해당하므로, 그러한 항은 $\binom{n}{k}$ 개이다. 따라서, $x_{i}=x, y_{i}=y, i=1, \ldots, n$ 으로 두면, 다음을 알 수 있다.

(x+y)^{n}=\sum_{k=0}^{n}\binom{n}{k} x^{k} y^{n-k}

Example

$(x+y)^{3}$ 을 전개하시오.

Solution

\begin{aligned} (x+y)^{3} & =\binom{3}{0} x^{0} y^{3}+\binom{3}{1} x^{1} y^{2}+\binom{3}{2} x^{2} y^{1}+\binom{3}{3} x^{3} y^{0} \\ & =y^{3}+3 x y^{2}+3 x^{2} y+x^{3} \end{aligned}

예시 4e

$n$ 개의 원소로 구성된 집합의 부분집합은 몇 개가 있는가? 풀이 크기가 $k$ 인 부분집합이 $\binom{n}{k}$ 개 있으므로, 원하는 답은 다음과 같다.

\sum_{k=0}^{n}\binom{n}{k}=(1+1)^{n}=2^{n}

이 결과는 집합의 각 원소에 0 또는 1을 할당하는 방식으로도 얻을 수 있다. 각 숫자 할당에는 부분집합이 일대일 방식으로 대응되는데, 이 부분집합은 값 1이 할당된 모든 원소로 구성된다. 가능한 할당이 $2^{n}$ 개이므로, 결과는 $2^{n}$ 이다.

우리는 0개의 원소로 구성된 집합(즉, 공집합)을 원래 집합의 부분집합으로 포함시켰다는 점에 유의해야 한다. 따라서 **적어도 1개의 원소를 포함하는 부분집합의 개수는 $2^{n}-1$ **이다.

1.5 Multinomial Coefficients

이 섹션에서는 다음 문제를 고려한다: $n$ 개의 서로 다른 항목을 각각 $n_{1}, n_{2}, \ldots, n_{r}$ 크기의 $r$ 개의 서로 다른 그룹으로 나누려고 한다. 여기서 $\sum_{i=1}^{r} n_{i}=n$ 이다. 몇 가지 다른 분할이 가능한가? 이 질문에 답하기 위해, 우리는 첫 번째 그룹에 대해 $\binom{n}{n_{1}}$ 가지 가능한 선택이 있다는 점에 주목한다. 첫 번째 그룹의 각 선택에 대해, 두 번째 그룹에 대해 $\binom{n-n_{1}}{n_{2}}$ 가지 가능한 선택이 있다. 처음 두 그룹의 각 선택에 대해, 세 번째 그룹에 대해 $\binom{n-n_{1}-n_{2}}{n_{3}}$ 가지 가능한 선택이 있으며, 이런 식으로 계속된다. 그러면 기본 계산 원리의 일반화된 버전에 따라 다음과 같은 수가 존재한다.

\begin{aligned} & \binom{n}{n_{1}}\binom{n-n_{1}}{n_{2}} \cdots\binom{n-n_{1}-n_{2}-\cdots-n_{r-1}}{n_{r}} \\ & =\frac{n!}{\left(n-n_{1}\right)!n_{1}!} \frac{\left(n-n_{1}\right)!}{\left(n-n_{1}-n_{2}\right)!n_{2}!} \cdots \frac{\left(n-n_{1}-n_{2}-\cdots-n_{r-1}\right)!}{0!n_{r}!} \\ & =\frac{n!}{n_{1}!n_{2}!\cdots n_{r}!} \end{aligned}

가능한 분할. 이 결과를 이해하는 또 다른 방법은 $n$ 개의 값 $1,1, \ldots, 1,2, \ldots, 2, \ldots$ , $r, \ldots, r$ 을 고려하는 것이다. 여기서 $i$ 는 $n_{i}$ 번 나타난다( $i=1, \ldots, r$ ). 이 값들의 모든 순열은 다음 방식으로 $n$ 개의 항목을 $r$ 개의 그룹으로 분할하는 것에 해당한다: 순열 $i_{1}, i_{2}, \ldots, i_{n}$ 이 항목 1을 그룹 $i_{1}$ 에, 항목 2를 그룹 $i_{2}$ 에 할당하는 식이라고 하자. 예를 들어, $n=8$ 이고 $n_{1}=4, n_{2}=3, n_{3}=1$ 인 경우, 순열 $1,1,2,3,2,1,2,1$ 은 항목 $1,2,6,8$ 을 첫 번째 그룹에, 항목 $3,5,7$ 을 두 번째 그룹에, 항목 4를 세 번째 그룹에 할당하는 것에 해당한다. 모든 순열이 항목의 분할을 생성하고, 모든 가능한 분할이 어떤 순열로부터 발생하기 때문에, $n$ 개의 항목을 크기가 $n_{1}, n_{2}, \ldots, n_{r}$ 인 $r$ 개의 서로 다른 그룹으로 분할하는 수는 $n_{1}$ 개가 같고, $n_{2}$ 개가 같고, $\ldots$ , $n_{r}$ 개가 같은 $n$ 개의 항목의 순열 수와 동일하다. 이는 섹션 1.3에서 $\frac{n!}{n_{1}!n_{2}!\cdots n_{r}!}$ 과 같다고 설명되었다.

Notation

만약 $n_{1}+n_{2}+\cdots+n_{r}=n$ 이라면, 우리는 $\binom{n}{n_{1}, n_{2}, \ldots, n_{r}}$ 을 다음과 같이 정의한다.

\binom{n}{n_{1}, n_{2}, \ldots, n_{r}}=\frac{n!}{n_{1}!n_{2}!\cdots n_{r}!}

따라서 $\binom{n}{n_{1}, n_{2}, \ldots, n_{r}}$ 은 $n$ 개의 서로 다른 객체를 각각 $n_{1}, n_{2}, \ldots, n_{r}$ 크기의 $r$ 개의 서로 다른 그룹으로 나누는 가능한 방법의 수를 나타낸다.

예제 5a

작은 도시의 경찰서는 10명의 경찰관으로 구성되어 있다. 만약 경찰서 방침이 5명의 경찰관은 거리를 순찰하고, 2명의 경찰관은 역에서 풀타임으로 근무하며, 3명의 경찰관은 역에서 예비 인력으로 대기하도록 한다면, 10명의 경찰관을 3개의 그룹으로 나누는 가능한 방법은 몇 가지인가? 풀이 가능한 분할의 수는 $\frac{10!}{5!2!3!}=2520$ 가지이다. 예제 5b

10명의 아이들을 각각 5명씩 $A$ 팀과 $B$ 팀으로 나누려고 한다. $A$ 팀은 한 리그에서 경기하고 $B$ 팀은 다른 리그에서 경기할 것이다. 몇 가지 다른 분할이 가능한가? 풀이 가능한 분할의 수는 $\frac{10!}{5!5!}=252$ 가지이다. 예제 5c

농구 경기를 하기 위해 놀이터의 10명의 아이들이 각각 5명씩 두 팀으로 나뉜다. 몇 가지 다른 분할이 가능한가?

풀이 이 예제는 예제 5b와 다르다는 점에 유의해야 한다. 왜냐하면 이제 두 팀의 순서는 중요하지 않기 때문이다. 즉, $A$ 팀이나 $B$ 팀이 있는 것이 아니라, 단순히 각각 5명으로 구성된 2개의 그룹으로 나뉘는 것이다. 따라서 원하는 답은 다음과 같다.

frac{10!/(5!5!)}{2!}=126

이항정리를 일반화한 다음 정리의 증명은 연습문제로 남겨둔다.

The multinomial theorem

\begin{aligned} & \left(x_{1}+x_{2}+\cdots+x_{r}\right)^{n}= \\ & \sum_{\substack{\left(n_{1}, \ldots, n_{r}\right): \\ n_{1}+\cdots+n_{r}}}\binom{n}{n_{1}, n_{2}, \ldots, n_{r}} x_{1}^{n_{1}} x_{2}^{n_{2}} \cdots x_{r}^{n_{r}} \end{aligned}

즉, 합은 $n_{1}+n_{2}+\cdots+n_{r}=n$ 을 만족하는 모든 음이 아닌 정수 값 벡터 ( $n_{1}, n_{2}, \ldots, n_{r}$ )에 대한 것이다.

$\binom{n}{n_{1}, n_{2}, \ldots, n_{r}}$ 은 **다항 계수(multinomial coefficients)**라고 알려져 있다.

Example 5d

$n=2^m$ 명의 플레이어가 참여하는 토너먼트의 첫 라운드에서, $n$ 명의 플레이어는 $n/2$ 개의 쌍으로 나뉘고, 각 쌍은 게임을 진행한다. 게임의 패자는 탈락하고 승자는 다음 라운드로 진출하며, 이 과정은 단 한 명의 플레이어가 남을 때까지 반복된다. 8명의 플레이어가 참여하는 토너먼트가 있다고 가정해 보자.

(a) 초기 라운드에서 가능한 결과는 몇 가지인가? (예를 들어, 1이 2를 이기고, 3이 4를 이기고, 5가 6을 이기고, 7이 8을 이기는 것이 하나의 결과이다.) (b) 모든 라운드에 대한 완전한 정보를 제공하는 토너먼트의 가능한 결과는 몇 가지인가?

풀이 초기 라운드에서 가능한 결과의 수를 결정하는 한 가지 방법은 먼저 해당 라운드의 가능한 페어링(pairing) 수를 결정하는 것이다. 이를 위해 8명의 플레이어를 첫 번째 쌍, 두 번째 쌍, 세 번째 쌍, 네 번째 쌍으로 나누는 방법의 수는 $\binom{8}{2,2,2,2}=\frac{8!}{2^{4}}$ 임을 주목하자. 따라서 4개의 쌍에 순서가 없을 때 가능한 페어링의 수는 $\frac{8!}{2^{4} 4!}$ 이다. 각 페어링에 대해 각 쌍에서 게임의 승자로 2가지 선택이 가능하므로, 라운드 1의 가능한 결과는 $\frac{8!2^{4}}{2^{4} 4!}=\frac{8!}{4!}$ 가지이다. [이를 확인하는 또 다른 방법은 4명의 승자를 선택하는 가능한 방법이 $\binom{8}{4}$ 가지이고, 각 선택에 대해 4명의 승자와 4명의 패자를 짝지을 수 있는 방법이 $4!$ 가지이므로, 첫 번째 라운드의 가능한 결과는 $4!\binom{8}{4}=\frac{8!}{4!}$ 가지임을 보여주는 것이다.]

마찬가지로, 라운드 1의 각 결과에 대해 라운드 2의 가능한 결과는 $\frac{4!}{2!}$ 가지이고, 처음 두 라운드의 각 결과에 대해 라운드 3의 가능한 결과는 $\frac{2!}{1!}$ 가지이다. 결과적으로, **일반화된 기본 계수 원리(generalized basic principle of counting)**에 따라 토너먼트의 가능한 결과는 $\frac{8!}{4!} \frac{4!}{2!} \frac{2!}{1!}=8!$ 가지이다. 실제로 동일한 논증을 사용하여 $n=2^m$ 명의 플레이어가 참여하는 토너먼트에는 $n!$ 가지의 가능한 결과가 있음을 보일 수 있다.

앞선 결과를 알고 있다면, 가능한 토너먼트 결과 집합과 $1, \ldots, n$ 의 순열(permutation) 집합 사이에 **일대일 대응(one-to-one correspondence)**이 있음을 보여줌으로써 더 직접적인 논증을 제시하는 것은 어렵지 않다. 이러한 대응을 얻기 위해, 모든 토너먼트 결과에 대해 플레이어의 순위를 다음과 같이 매긴다: 토너먼트 우승자에게는 1위, 결승전 패자에게는 2위를 부여한다. 준결승전에서 패한 두 플레이어 중 1위 플레이어에게 패한 플레이어에게는 3위, 2위 플레이어에게 패한 플레이어에게는 4위를 부여한다. 8강전에서 패한 네 플레이어 중 1위 플레이어에게 패한 플레이어에게는 5위, 2위 플레이어에게 패한 플레이어에게는 6위, 3위 플레이어에게 패한 플레이어에게는 7위, 4위 플레이어에게 패한 플레이어에게는 8위를 부여한다. 이 방식으로 계속 진행하면 각 플레이어에게 순위가 부여된다. (더 간결한 설명은 토너먼트 우승자에게 1위를 부여하고, $2^k$ 개의 경기가 있는 라운드에서 패한 플레이어의 순위는 $2^k$ 에 자신을 이긴 플레이어의 순위를 더한 값으로 정의하는 것이다. 여기서 $k=0, \ldots, m-1$ 이다.) 이러한 방식으로 토너먼트 결과는 순열 $i_1, i_2, \ldots, i_n$ 으로 표현될 수 있으며, 여기서 $i_j$ 는 $j$ 위를 부여받은 플레이어이다. 서로 다른 토너먼트 결과는 서로 다른 순열을 생성하고, 각 순열에 대해 토너먼트 결과가 존재하므로, 가능한 토너먼트 결과의 수는 $1, \ldots, n$ 의 순열 수와 동일하다.

Example 5e

\begin{aligned} \left(x_{1}+x_{2}+x_{3}\right)^{2}= & \binom{2}{2,0,0} x_{1}^{2} x_{2}^{0} x_{3}^{0}+\binom{2}{0,2,0} x_{1}^{0} x_{2}^{2} x_{3}^{0} \\ & +\binom{2}{0,0,2} x_{1}^{0} x_{2}^{0} x_{3}^{2}+\binom{2}{1,1,0} x_{1}^{1} x_{2}^{1} x_{3}^{0} \\ & +\binom{2}{1,0,1} x_{1}^{1} x_{2}^{0} x_{3}^{1}+\binom{2}{0,1,1} x_{1}^{0} x_{2}^{1} x_{3}^{1} \\ = & x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+2 x_{1} x_{2}+2 x_{1} x_{3}+2 x_{2} x_{3} \end{aligned}

*1.6 The Number of Integer Solutions of Equations

한 사람이 Ticonderoga 호수에서 낚시를 갔는데, 이 호수에는 송어, 메기, 농어, 전갱이의 네 가지 종류의 물고기가 서식한다. 낚시 결과가 잡힌 각 물고기의 수라고 할 때, 총 10마리의 물고기를 잡았을 때 가능한 결과의 수를 결정해 보자. 이를 위해, 낚시 결과를 벡터 $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)$ 로 나타낼 수 있음을 주목하자. 여기서 $x_{1}$ 은 잡힌 송어의 수, $x_{2}$ 는 메기의 수, $x_{3}$ 는 농어의 수, $x_{4}$ 는 전갱이의 수이다. 따라서 총 10마리의 물고기를 잡았을 때 가능한 결과의 수는 합이 10이 되는 음이 아닌 벡터 $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)$ 의 수이다.

더 일반적으로, $r$ 가지 종류의 물고기가 있고 총 $n$ 마리를 잡았다고 가정하면, 가능한 결과의 수는 다음을 만족하는 음이 아닌 정수 값 벡터 $x_{1}, \ldots, x_{r}$ 의 수와 같다.

x_{1}+x_{2}+\ldots+x_{r}=n

이 수를 계산하기 위해, 먼저 위 식을 만족하는 양의 정수 값 벡터 $x_{1}, \ldots, x_{r}$ 의 수를 고려해 보자. 이 수를 결정하기 위해, $n$ 개의 연속된 0이 한 줄로 나열되어 있다고 가정해 보자.

000 \ldots 00

인접한 0들 사이의 $n-1$ 개 공간 중 $r-1$ 개를 선택하는 것은 (그림 1.2 참조) 첫 번째 선택된 공간 앞의 0의 수를 $x_{1}$ 로, 첫 번째와 두 번째 선택된 공간 사이의 0의 수를 $x_{2}$ 로, ..., 마지막 선택된 공간 뒤의 0의 수를 $x_{n}$ 으로 설정함으로써 (6.1)의 양의 해에 해당함을 주목하자.

0 \wedge 0 \wedge 0 \wedge \ldots \wedge 0 \wedge 0

$n$ 개의 객체 0 $r-1$ 개의 공간 $\wedge$ 를 선택한다.

Figure 1.2 양의 해의 수.

예를 들어, $n=8$ 이고 $r=3$ 인 경우 (선택은 점으로 표시됨) 다음과 같은 선택은

0.0000 .000

해 $x_{1}=1, x_{2}=4, x_{3}=3$ 에 해당한다. (6.1)의 양의 해는 $n-1$ 개의 인접한 공간 중 $r-1$ 개를 선택하는 것과 일대일 방식으로 대응하므로, 서로 다른 양의 해의 수는 $n-1$ 개의 인접한 공간 중 $r-1$ 개를 선택하는 서로 다른 방법의 수와 같다. 결과적으로, 다음 명제를 얻는다.

Proposition 6.1

Proposition 6.2

Example 6a

Example 6b

방정식 $x_{1}+x_{2}+\cdots+x_{r}=n \quad x_{i}>0, \quad i=1, \ldots, r$ 을 만족하는 서로 다른 양의 정수 값 벡터 $\left(x_{1}, x_{2}, \ldots, x_{r}\right)$ 는 $\binom{n-1}{r-1}$ 개 존재한다.

음이 아닌 (양의 해와는 반대되는) 해의 수를 얻기 위해, $x_{1}+x_{2}+\cdots+x_{r}=n$ 의 음이 아닌 해의 수는 $y_{1}+\cdots+y_{r}=n+r$ 의 양의 해의 수와 같음을 주목하자 (이는 $y_{i}=x_{i}+1, i=1, \ldots, r$ 로 설정함으로써 알 수 있다). 따라서 명제 6.1로부터 다음 명제를 얻는다. 방정식 $x_{1}+x_{2}+\cdots+x_{r}=n$ 을 만족하는 서로 다른 음이 아닌 정수 값 벡터 $\left(x_{1}, x_{2}, \ldots, x_{r}\right)$ 는 $\binom{n+r-1}{r-1}$ 개 존재한다.

따라서 명제 6.2를 사용하면, Ticonderoga 호수에서 총 10마리의 물고기를 잡았을 때 가능한 결과는 $\binom{13}{3}=286$ 가지임을 알 수 있다.

$x_{1}+x_{2}=3$ 의 서로 다른 음이 아닌 정수 값 해는 몇 가지가 가능한가? 해답 $\binom{3+2-1}{2-1}=4$ 가지 해가 있다: $(0,3),(1,2),(2,1),(3,0)$ . 한 투자자가 4가지 가능한 투자처에 20,000달러를 투자하려고 한다. 각 투자는 1,000달러 단위로 이루어져야 한다. 총 20,000달러를 모두 투자해야 한다면, 몇 가지 다른 투자 전략이 가능한가? 모든 돈을 투자할 필요가 없다면 어떻게 되는가?

해답 $x_{i}, i=1,2,3,4$ 를 투자처 $i$ 에 투자된 천 달러 단위의 금액이라고 하면, 모든 돈을 투자해야 할 때 $x_{1}, x_{2}, x_{3}, x_{4}$ 는 다음 방정식을 만족하는 정수이다.

x_{1}+x_{2}+x_{3}+x_{4}=20 \quad x_{i} \geq 0

따라서 명제 6.2에 의해 $\binom{23}{3}=1771$ 가지 가능한 투자 전략이 있다. 모든 돈을 투자할 필요가 없다면, $x_{5}$ 를 예비금으로 남겨둔 금액이라고 할 때, 전략은 다음 방정식을 만족하는 음이 아닌 정수 값 벡터 ( $x_{1}, x_{2}, x_{3}, x_{4}, x_{5}$ )이다.

x_{1}+x_{2}+x_{3}+x_{4}+x_{5}=20

따라서 명제 6.2에 의해 이제 $\binom{24}{4}=10,626$ 가지 가능한 전략이 있다.

Example 6c

Example 6d

$\left(x_{1}+x_{2}+\cdots+x_{r}\right)^{n}$ 의 다항식 전개에는 몇 개의 항이 있는가?

Solution

\left(x_{1}+x_{2}+\cdots+x_{r}\right)^{n}=\sum\binom{n}{n_{1}, \ldots, n_{r}} x_{1}^{n_{1}} \cdots x_{r}^{n_{r}}

여기서 합은 $n_{1}+\cdots+ n_{r}=n$ 을 만족하는 모든 음이 아닌 정수 값 ( $n_{1}, \ldots, n_{r}$ )에 대한 것이다. 따라서 Proposition 6.2에 의해 이러한 항은 $\binom{n+r-1}{r-1}$ 개 존재한다.

다시 Example 4c를 살펴보자. 여기서는 $n$ 개의 항목 중 $m$ 개는 (구분 불가능하며) 불량품이고, 나머지 $n-m$ 개는 (역시 구분 불가능하며) 정상 작동하는 항목이다. 우리의 목표는 두 불량품이 서로 옆에 있지 않는 선형 순서의 수를 결정하는 것이다. 이 수를 결정하기 위해, 불량품들이 자체적으로 줄지어 있고 이제 정상 작동하는 항목들이 제자리에 놓인다고 상상해 보자. $x_{1}$ 을 첫 번째 불량품 왼쪽에 있는 정상 작동 항목의 수, $x_{2}$ 를 처음 두 불량품 사이에 있는 정상 작동 항목의 수 등으로 나타내자. 즉, 도식적으로 다음과 같다.

x_{1} 0 x_{2} 0 \cdots x_{m} 0 x_{m+1}

이제 $x_{i}>0, i=2, \ldots, m$ 인 한, 모든 불량품 쌍 사이에 적어도 하나의 정상 작동 항목이 있을 것이다. 따라서 조건을 만족하는 결과의 수는 다음 방정식을 만족하는 벡터 $x_{1}, \ldots, x_{m+1}$ 의 수와 같다.

x_{1}+\cdots+x_{m+1}=n-m \quad x_{1} \geq 0, x_{m+1} \geq 0, x_{i}>0, i=2, \ldots, m

그러나 $y_{1}=x_{1}+1, y_{i}=x_{i}, i=2, \ldots, m, y_{m+1}=x_{m+1}+1$ 로 두면, 이 수는 다음 방정식을 만족하는 양의 벡터 $\left(y_{1}, \ldots, y_{m+1}\right)$ 의 수와 같다는 것을 알 수 있다.

y_{1}+y_{2}+\cdots+y_{m+1}=n-m+2

따라서 Proposition 6.1에 의해 이러한 결과는 $\binom{n-m+1}{m}$ 개 존재하며, 이는 Example 4c의 결과와 일치한다.

이제 각 불량품 쌍이 적어도 2개의 정상 작동 항목으로 분리되는 결과의 수에 관심이 있다고 가정해 보자. 이전에 적용된 것과 동일한 추론에 따르면, 이는 다음 방정식을 만족하는 벡터의 수와 같을 것이다.

x_{1}+\cdots+x_{m+1}=n-m \quad x_{1} \geq 0, x_{m+1} \geq 0, x_{i} \geq 2, i=2, \ldots, m

$y_{1}=x_{1}+1, y_{i}=x_{i}-1, i=2, \ldots, m, y_{m+1}=x_{m+1}+1$ 로 두면, 이는 다음 방정식의 양의 해의 수와 같다는 것을 알 수 있다.

y_{1}+\cdots+y_{m+1}=n-2 m+3

따라서 Proposition 6.1에 의해 이러한 결과는 $\binom{n-2 m+2}{m}$ 개 존재한다.

Summary

counting states의 기본 원칙은 두 단계로 구성된 실험에서 1단계의 가능한 결과가 $n$ 가지이고, 이 $n$ 가지 결과 각각에 대해 2단계의 가능한 결과가 $m$ 가지라면, 해당 실험의 가능한 결과는 $nm$ 가지라는 것이다.

$n$ 개의 항목을 선형으로 배열하는 가능한 경우의 수는 $n!=n(n-1) \cdots 3 \cdot 2 \cdot 1$ 이다. $0!$ 은 1로 정의된다.

$0 \leq i \leq n$ 일 때,

\binom{n}{i}=\frac{n!}{(n-i)!i!}

로 정의하고, 그 외의 경우에는 0으로 정의한다. 이 값은 크기 $n$ 인 집합에서 크기 $i$ 인 서로 다른 부분 집합을 선택할 수 있는 경우의 수를 나타낸다. 이는 **이항 정리(binomial theorem)**에서 중요한 역할을 하므로 **이항 계수(binomial coefficient)**라고 불리며, 이항 정리는 다음과 같이 표현된다:

(x+y)^{n}=\sum_{i=0}^{n}\binom{n}{i} x^{i} y^{n-i}

합이 $n$ 이 되는 음이 아닌 정수 $n_{1}, \ldots, n_{r}$ 에 대해,

\binom{n}{n_{1}, n_{2}, \ldots, n_{r}}=\frac{n!}{n_{1}!n_{2}!\cdots n_{r}!}

는 $n$ 개의 항목을 크기가 $n_{1}, n_{2} \ldots, n_{r}$ 인 $r$ 개의 서로 다른 중복되지 않는 부분 집합으로 나누는 경우의 수이다. 이 값들을 **다항 계수(multinomial coefficients)**라고 한다.

Problems

(a) 첫 2자리는 문자를 위한 것이고 나머지 5자리는 숫자를 위한 것이라면, 몇 개의 다른 7자리 차량 번호판이 가능한가? (b) 단일 번호판에 문자나 숫자가 반복될 수 없다는 가정하에 (a)를 반복하라.
주사위를 네 번 굴릴 때 가능한 결과 시퀀스는 몇 가지인가? 예를 들어, 첫 번째 굴림에서 3, 두 번째에서 4, 세 번째에서 3, 네 번째에서 1이 나왔다면 결과는 3,4,3,1이라고 말한다.
20명의 작업자가 20개의 다른 작업에 각각 한 명씩 배정될 것이다. 몇 가지 다른 배정이 가능한가?
John, Jim, Jay, Jack은 4가지 악기로 구성된 밴드를 결성했다. 만약 각 소년이 4가지 악기를 모두 연주할 수 있다면, 몇 가지 다른 편성이 가능한가? 만약 John과 Jim은 4가지 악기를 모두 연주할 수 있지만, Jay와 Jack은 각각 피아노와 드럼만 연주할 수 있다면 어떠한가?
수년 동안 미국과 캐나다의 전화 지역 번호는 세 자리 숫자의 시퀀스로 구성되었다. 첫 번째 숫자는 2에서 9 사이의 정수였고, 두 번째 숫자는 0 또는 1이었으며, 세 번째 숫자는 1에서 9 사이의 임의의 정수였다. 몇 개의 지역 번호가 가능했는가? 4로 시작하는 지역 번호는 몇 개가 가능했는가?
잘 알려진 동요는 다음과 같이 시작한다: "내가 세인트 아이브스로 가고 있을 때 아내 7명과 함께 있는 남자를 만났네. 각 아내는 자루 7개를 가지고 있었네. 각 자루에는 고양이 7마리가 있었네. 각 고양이에는 새끼 고양이 7마리가 있었네. . ." 여행자는 몇 마리의 새끼 고양이를 만났는가?
(a) 3명의 소년과 3명의 소녀가 한 줄로 앉을 수 있는 방법은 몇 가지인가? (b) 소년들과 소녀들이 각각 함께 앉아야 한다면, 3명의 소년과 3명의 소녀가 한 줄로 앉을 수 있는 방법은 몇 가지인가? (c) 소년들만 함께 앉아야 한다면 몇 가지 방법이 있는가? (d) 같은 성별의 두 사람이 함께 앉을 수 없다면 몇 가지 방법이 있는가?
다음 글자들로 만들 수 있는 다른 글자 배열은 몇 가지인가? (a) Fluke? (b) Propose? (c) Mississippi? (d) Arrange?
어떤 아이가 12개의 블록을 가지고 있는데, 그 중 6개는 검은색, 4개는 빨간색, 1개는 흰색, 1개는 파란색이다. 아이가 블록을 한 줄로 놓는다면, 몇 가지 배열이 가능한가?
8명이 한 줄로 앉을 수 있는 방법은 몇 가지인가? (a) 좌석 배치에 제한이 없는 경우? (b) A와 B가 서로 옆에 앉아야 하는 경우? (c) 4명의 남자와 4명의 여자가 있고, 남자 2명 또는 여자 2명이 서로 옆에 앉을 수 없는 경우? (d) 5명의 남자가 있고 그들이 서로 옆에 앉아야 하는 경우? (e) 4쌍의 부부가 있고 각 부부가 함께 앉아야 하는 경우?
3권의 소설, 2권의 수학책, 1권의 화학책을 책장에 배열할 수 있는 방법은 몇 가지인가? (a) 책을 어떤 순서로든 배열할 수 있는 경우? (b) 수학책은 함께 있어야 하고 소설은 함께 있어야 하는 경우? (c) 소설은 함께 있어야 하지만 다른 책들은 어떤 순서로든 배열할 수 있는 경우?
30명의 학생들 중에서 선정된 학생들에게 5개의 개별 상(최고 장학금, 최고 리더십 자질 등)이 수여될 것이다. 몇 가지 다른 결과가 가능한가? (a) 한 학생이 여러 개의 상을 받을 수 있는 경우? (b) 각 학생이 최대 1개의 상을 받을 수 있는 경우?
20명의 그룹을 생각해보자. 만약 모든 사람이 서로 악수를 한다면, 몇 번의 악수가 일어나는가?
5장의 포커 패는 몇 가지가 있는가?
댄스 수업은 22명의 학생으로 구성되어 있으며, 그 중 10명은 여성이고 12명은 남성이다. 만약 5명의 남성과 5명의 여성을 선택한 다음 짝을 짓는다면, 몇 가지 결과가 가능한가?
한 학생이 6권의 수학책, 7권의 과학책, 4권의 경제학책 컬렉션에서 2권의 책을 팔아야 한다. 몇 가지 선택이 가능한가? (a) 두 권의 책이 같은 과목인 경우? (b) 책들이 다른 과목인 경우?
7개의 다른 선물을 10명의 어린이에게 나누어 줄 것이다. 어떤 어린이도 한 개 이상의 선물을 받지 않는다면, 몇 가지 다른 결과가 가능한가?
5명의 공화당원, 6명의 민주당원, 4명의 무소속으로 구성된 그룹에서 공화당원 2명, 민주당원 2명, 무소속 3명으로 구성된 7명의 위원회를 선출할 것이다. 몇 개의 위원회가 가능한가?
8명의 여성과 6명의 남성으로 구성된 그룹에서 3명의 남성과 3명의 여성으로 구성된 위원회를 구성할 것이다. 몇 가지 다른 위원회가 가능한가? (a) 남자 2명이 함께 봉사하기를 거부하는 경우? (b) 여자 2명이 함께 봉사하기를 거부하는 경우? (c) 남자 1명과 여자 1명이 함께 봉사하기를 거부하는 경우?
한 사람에게는 8명의 친구가 있는데, 그 중 5명이 파티에 초대될 것이다. (a) 친구 중 2명이 싸워서 함께 참석하지 않을 경우 몇 가지 선택이 가능한가? (b) 친구 중 2명이 함께만 참석할 경우 몇 가지 선택이 가능한가?
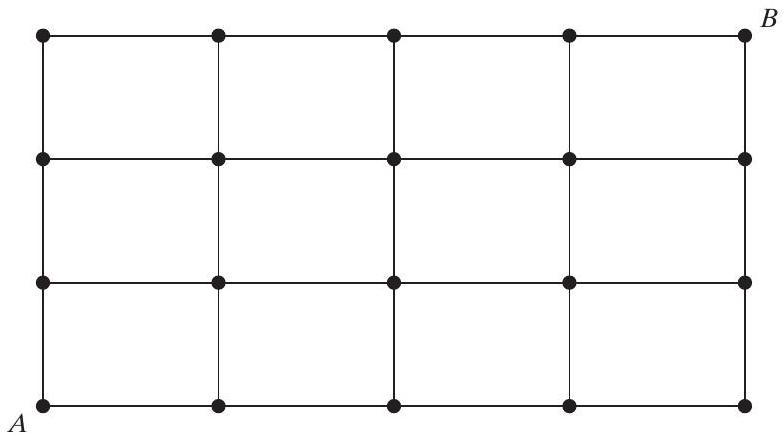
다음 열 상단에 표시된 점들의 격자를 고려해보자. A로 표시된 점에서 시작하여 각 이동에서 한 단계 위로 또는 한 단계 오른쪽으로 갈 수 있다고 가정하자. 이 절차는 B로 표시된 점에 도달할 때까지 계속된다. A에서 B까지 가능한 다른 경로는 몇 가지인가? 힌트: A에서 B에 도달하려면 오른쪽으로 4단계, 위로 3단계를 이동해야 한다.
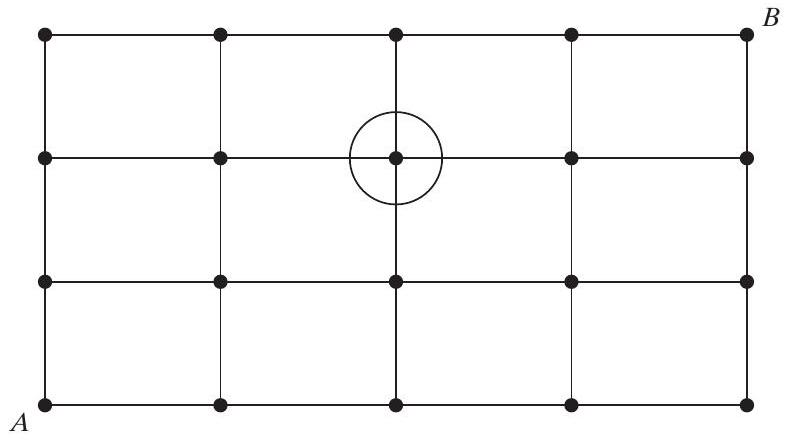
문제 21에서, 다음 격자에서 동그라미 친 점을 통과하는 A에서 B까지의 다른 경로는 몇 가지인가?
꿈 연구를 수행하는 심리학 연구실에는 각 방에 2개의 침대가 있는 3개의 방이 있다. 3쌍의 일란성 쌍둥이가 이 6개의 침대에 배정되어 각 쌍둥이 세트가 같은 방의 다른 침대에서 잠을 자야 한다면, 몇 가지 배정이 가능한가?
$\left(3 x^{2}+y\right)^{5}$ 를 전개하라.
브리지 게임은 4명의 플레이어가 각자 13장의 카드를 받는 방식으로 진행된다. 몇 가지 브리지 딜이 가능한가?
$\left(x_{1}+2 x_{2}+3 x_{3}\right)^{4}$ 를 전개하라.
12명의 사람들을 각각 3명, 4명, 5명의 3개 위원회로 나눈다면, 몇 가지 분할이 가능한가?
8명의 신임 교사를 4개의 학교에 나눈다면, 몇 가지 분할이 가능한가? 각 학교가 2명의 교사를 받아야 한다면 어떠한가?
10명의 역도 선수가 팀 역도 대회에 참가하고 있다. 선수 중 3명은 미국 출신, 4명은 러시아 출신, 2명은 중국 출신, 1명은 캐나다 출신이다. 채점이 선수들의 개별 신원이 아닌 그들이 대표하는 국가를 고려한다면, 점수 관점에서 몇 가지 다른 결과가 가능한가? 미국이 상위 3명에 1명, 하위 3명에 2명의 경쟁자를 두는 결과에 해당하는 다른 결과는 몇 가지인가?
러시아, 프랑스, 영국, 미국을 포함한 10개국 대표단이 한 줄로 앉을 것이다. 프랑스 대표와 영국 대표가 서로 옆에 앉고 러시아 대표와 미국 대표가 서로 옆에 앉지 않아야 한다면, 몇 가지 다른 좌석 배치가 가능한가? *31. 8개의 동일한 칠판을 4개의 학교에 나눈다면, 몇 가지 분할이 가능한가? 각 학교가 최소 1개의 칠판을 받아야 한다면 몇 가지인가? *32. 엘리베이터가 8명의 사람(엘리베이터 운전사는 제외)과 함께 지하에서 출발하여 6층인 꼭대기 층에 도달할 때까지 모두 내린다. 모든 사람이 운전사에게 똑같이 보인다면, 운전사가 사람들이 엘리베이터를 떠나는 것을 인지할 수 있는 방법은 몇 가지인가? 8명의 사람이 5명의 남자와 3명의 여자로 구성되어 있고 운전사가 남자와 여자를 구별할 수 있다면 어떠한가?

Theoretical Exercises

기본 counting principle의 일반화된 버전을 증명하시오.
두 가지 실험을 수행한다. 첫 번째 실험은 $m$ 가지 가능한 결과 중 하나를 낼 수 있다. 첫 번째 실험의 결과가 $i$ 일 때, 두 번째 실험은 $n_i$ 가지 가능한 결과 중 하나를 낼 수 있다 ( $i=1,2, \ldots, m$ ). 두 실험의 가능한 결과의 수는 얼마인가?
$n$ 개의 객체 집합에서 $r$ 개의 객체를 선택할 때, 선택 순서가 고려된다면 몇 가지 방법이 있는가?
$n$ 개의 공 중 $r$ 개가 검은색이고 $n-r$ 개가 흰색인 경우, $\binom{n}{r}$ 가지의 서로 다른 선형 배열이 가능하다. 이 사실에 대한 조합론적 설명을 제시하시오.
각 $x_i$ 가 0 또는 1이고 다음을 만족하는 벡터 $\left(x_{1}, \ldots, x_{n}\right)$ 의 수를 결정하시오.

\sum_{i=1}^{n} x_{i} \geq k

각 $x_i$ 가 $1 \leq x_i \leq n$ 을 만족하는 양의 정수이고 $x_{1}<x_{2}< \cdots<x_{k}$ 인 벡터 $x_{1}, \ldots, x_{k}$ 는 몇 개가 있는가?
방정식 (4.1)에 대한 해석적 증명을 제시하시오.
다음을 증명하시오.

\begin{aligned} \binom{n+m}{r}= & \binom{n}{0}\binom{m}{r}+\binom{n}{1}\binom{m}{r-1} \\ & +\cdots+\binom{n}{r}\binom{m}{0} \end{aligned}

*33. 4가지 가능한 기회에 투자해야 하는 $20,000달러가 있다. 각 투자는$ 1000달러 단위로 정수여야 하며, 이러한 기회에 투자하려면 최소 투자액이 필요하다. 최소 투자액은 $2000,$ 2000, $3000,$ 4000이다. 다음 경우에 몇 가지 다른 투자 전략이 가능한가? (a) 각 기회에 투자를 해야 하는 경우 (b) 4가지 기회 중 최소 3가지에 투자를 해야 하는 경우 *34. 5가지 종류의 물고기가 있는 호수에서 10마리의 물고기를 잡았다고 가정하자. (a) 5가지 종류 각각의 잡힌 물고기 수를 명시하는 결과는 몇 가지가 가능한가? (b) 잡힌 10마리의 물고기 중 3마리가 송어인 경우 몇 가지 결과가 가능한가? (c) 잡힌 10마리 중 최소 2마리가 송어인 경우 몇 가지 결과가 가능한가?

힌트: $n$ 명의 남성과 $m$ 명의 여성으로 구성된 그룹을 고려하시오. 크기가 $r$ 인 그룹은 몇 개가 가능한가? 9. Theoretical Exercise 8을 사용하여 다음을 증명하시오.

\binom{2 n}{n}=\sum_{k=0}^{n}\binom{n}{k}^{2}

$n$ 명의 사람들로 구성된 그룹에서 $k \leq n$ 인 $k$ 명의 위원회를 선택하고, 그 중 한 명을 위원장으로 지정한다고 가정하자. (a) 먼저 위원회 선택에 초점을 맞춘 다음 위원장 선택에 초점을 맞춰, $\binom{n}{k} k$ 가지 가능한 선택이 있음을 주장하시오. (b) 먼저 비위원장 위원회 구성원 선택에 초점을 맞춘 다음 위원장 선택에 초점을 맞춰, $\binom{n}{k-1}(n-k+1)$ 가지 가능한 선택이 있음을 주장하시오. (c) 먼저 위원장 선택에 초점을 맞춘 다음 다른 위원회 구성원 선택에 초점을 맞춰, $n\binom{n-1}{k-1}$ 가지 가능한 선택이 있음을 주장하시오. (d) (a), (b), (c) 부분에서 다음을 결론 내리시오.

k\binom{n}{k}=(n-k+1)\binom{n}{k-1}=n\binom{n-1}{k-1}

(e) $\binom{m}{r}$ 의 factorial definition을 사용하여 (d) 부분의 항등식을 확인하시오. 11. 다음 항등식은 Fermat의 조합론적 항등식으로 알려져 있다:

\binom{n}{k}=\sum_{i=k}^{n}\binom{i-1}{k-1} \quad n \geq k

이 항등식을 확립하기 위한 조합론적 논증을 제시하시오 (계산은 필요하지 않다). 힌트: 1부터 $n$ 까지의 숫자 집합을 고려하시오. $i$ 를 가장 높은 번호의 구성원으로 갖는 크기 $k$ 의 부분집합은 몇 개가 있는가? 12. 다음 조합론적 항등식을 고려하시오.

\sum_{k=1}^{n} k\binom{n}{k}=n \cdot 2^{n-1}

(a) $n$ 명의 사람 집합을 고려하고, 모든 크기의 위원회와 위원장을 선택하는 가능한 방법의 수를 두 가지 방식으로 결정하여 이 항등식에 대한 조합론적 논증을 제시하시오. 힌트: (i) 크기 $k$ 의 위원회와 그 위원장을 선택하는 가능한 방법은 몇 가지가 있는가? (ii) 위원장과 다른 위원회 구성원을 선택하는 가능한 방법은 몇 가지가 있는가? (b) $n=1,2,3,4,5$ 에 대해 다음 항등식을 확인하시오.

\sum_{k=1}^{n}\binom{n}{k} k^{2}=2^{n-2} n(n+1)

위의 조합론적 증명을 위해 $n$ 명의 사람 집합을 고려하고, 항등식의 양변이 위원회, 위원장, 그리고 비서(위원장과 동일할 수 있음)를 선택하는 서로 다른 방법의 수를 나타냄을 주장하시오.

Hint:

(i) 정확히 $k$ 명의 위원으로 구성된 위원회를 구성하는 서로 다른 선택의 수는 몇 가지인가? (ii) 위원장과 총무가 동일한 서로 다른 선택의 수는 몇 가지인가? (답: $n 2^{n-1}$ .) (iii) 위원장과 총무가 다른 서로 다른 선택의 수는 몇 가지인가? (c) 이제 다음을 논증하라.

\sum_{k=1}^{n}\binom{n}{k} k^{3}=2^{n-3} n^{2}(n+3)

$n>0$ 일 때, 다음을 보여라.

\sum_{i=0}^{n}(-1)^{i}\binom{n}{i}=0

힌트: **이항 정리(binomial theorem)**를 사용하라. 14. $n$ 명의 사람으로 구성된 집합에서 $j$ 명의 위원회를 선택하고, 이 위원회에서 $i$ 명의 소위원회를 선택한다 ( $i \leq j$ ). (a) 위원회와 소위원회를 선택하는 가능한 경우의 수를 두 가지 방법으로 계산하여 **조합 항등식(combinatorial identity)**을 도출하라. 첫 번째 방법은 위원회를 먼저 선택한 다음 소위원회를 선택하는 것이고, 두 번째 방법은 소위원회를 먼저 선택한 다음 위원회의 나머지 구성원을 선택하는 것이다. (b) (a) 부분을 사용하여 다음 조합 항등식을 증명하라.

\sum_{j=i}^{n}\binom{n}{j}\binom{j}{i}=\binom{n}{i} 2^{n-i} \quad i \leq n

\sum_{j=i}^{n}\binom{n}{j}\binom{j}{i}(-1)^{n-j}=0 \quad i<n

$H_{k}(n)$ 을 각 $x_{i}$ 가 $1 \leq x_{i} \leq n$ 을 만족하는 양의 정수이고 $x_{1} \leq x_{2} \leq \cdots \leq x_{k}$ 인 벡터 $x_{1}, \ldots, x_{k}$ 의 개수라고 하자. (a) 어떠한 계산도 없이 다음을 논증하라.

\begin{aligned} H_{1}(n) & =n \\ H_{k}(n) & =\sum_{j=1}^{n} H_{k-1}(j) \quad k>1 \end{aligned}

힌트: $x_{k}=j$ 인 벡터는 몇 개 있는가? (b) 앞선 **재귀(recursion)**를 사용하여 $H_{3}(5)$ 를 계산하라.

힌트: 먼저 $n=1,2,3,4,5$ 에 대해 $H_{2}(n)$ 을 계산하라. 16. $n$ 명의 참가자가 참여하는 토너먼트를 고려하자. 결과는 동점을 허용하는 참가자들의 순서이다. 즉, 결과는 플레이어들을 그룹으로 나눈다. 첫 번째 그룹은 1위를 차지한 플레이어들로 구성되고, 다음 그룹은 다음으로 좋은 순위를 차지한 플레이어들로 구성되는 식이다. $N(n)$ 을 가능한 서로 다른 결과의 수라고 하자. 예를 들어, $N(2)=3$ 이다. 왜냐하면 2명의 참가자가 있는 토너먼트에서 플레이어 1이 단독 1위일 수 있고, 플레이어 2가 단독 1위일 수 있으며, 또는 둘이 공동 1위일 수 있기 때문이다. (a) $n=3$ 일 때 가능한 모든 결과를 나열하라. (b) $N(0)$ 을 1로 정의하고, 어떠한 계산도 없이 다음을 논증하라.

N(n)=\sum_{i=1}^{n}\binom{n}{i} N(n-i)

힌트: $i$ 명의 플레이어가 꼴찌를 차지하는 결과는 몇 개 있는가? (c) (b) 부분의 공식이 다음 공식과 동등함을 보여라.

N(n)=\sum_{i=0}^{n-1}\binom{n}{i} N(i)

(d) **재귀(recursion)**를 사용하여 $N(3)$ 과 $N(4)$ 를 구하라. 17. $\binom{n}{r}=\binom{n}{r, n-r}$ 인 이유에 대한 **조합론적 설명(combinatorial explanation)**을 제시하라. 18. 다음을 논증하라.

\begin{aligned} \binom{n}{n_{1}, n_{2}, \ldots, n_{r}}= & \binom{n-1}{n_{1}-1, n_{2}, \ldots, n_{r}} \\ & +\binom{n-1}{n_{1}, n_{2}-1, \ldots, n_{r}}+\cdots \\ & +\binom{n-1}{n_{1}, n_{2}, \ldots, n_{r}-1} \end{aligned}

힌트: 방정식 (4.1)을 확립하는 데 사용된 것과 유사한 논증을 사용하라.

Self-Test Problems and Exercises

문자 $\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}, \mathrm{E}, \mathrm{F}$ 를 사용하여 만들 수 있는 서로 다른 선형 배열의 수는 다음과 같다: (a) A와 B가 서로 옆에 있는 경우: (b) A가 B보다 앞에 있는 경우: (c) A가 B보다 앞에 있고 B가 C보다 앞에 있는 경우: (d) A가 B보다 앞에 있고 C가 D보다 앞에 있는 경우: (e) A와 B가 서로 옆에 있고 C와 D도 서로 옆에 있는 경우: (f) E가 마지막에 오지 않는 경우:
4명의 미국인, 3명의 프랑스인, 3명의 영국인이 한 줄로 앉을 때, 같은 국적의 사람들이 반드시 옆에 앉아야 한다면 몇 가지 좌석 배치가 가능한가?
10명으로 구성된 클럽에서 회장, 총무, 비서(모두 다른 사람)를 선출해야 한다. 가능한 임원 선택의 수는 다음과 같다: (a) 제한이 없는 경우: (b) A와 B는 함께 봉사하지 않는 경우: (c) C와 D는 함께 봉사하거나 전혀 봉사하지 않는 경우: (d) E는 반드시 임원이어야 하는 경우: (e) F는 회장일 경우에만 봉사하는 경우:
한 학생이 시험에서 10문제 중 7문제를 풀어야 한다. 이 학생이 선택할 수 있는 경우의 수는 몇 가지인가? 처음 5문제 중 적어도 3문제를 풀어야 한다면 몇 가지인가?
한 남자가 7개의 선물을 3명의 자녀에게 나누어 주는데, 맏이가 3개의 선물을 받고 다른 자녀들은 각각 2개씩 받는 경우의 수는 몇 가지인가?
다항정리를 증명하시오. *20. $n$ 개의 동일한 공을 $r$ 개의 항아리에 분배하는 방법의 수는 몇 가지인가? 단, 각 $i=1, \ldots, r$ 에 대해 $i$ 번째 항아리에는 적어도 $m_{i}$ 개의 공이 포함되어야 한다. $n \geq \sum_{i=1}^{r} m_{i}$ 라고 가정한다. *21. 다음 방정식의 해 중 정확히 $k$ 개의 $x_{i}$ 가 0인 경우의 수가 정확히 $\binom{r}{k}\binom{n-1}{n-r+k}$ 임을 논증하시오.

x_{1}+x_{2}+\cdots+x_{r}=n

*22. $n$ 개의 변수로 구성된 함수 $f\left(x_{1}, \ldots, x_{n}\right)$ 를 고려하시오. $f$ 가 가질 수 있는 $r$ 차 편도함수의 수는 몇 가지인가? *23. 각 $x_{i}$ 가 음이 아닌 정수이고 다음을 만족하는 벡터 $\left(x_{1}, \ldots, x_{n}\right)$ 의 수를 결정하시오.

\sum_{i=1}^{n} x_{i} \leq k

7자리 자동차 번호판에서 3자리는 문자이고 4자리는 숫자일 때, 가능한 서로 다른 번호판의 수는 몇 가지인가? 문자와 숫자의 반복이 허용되고, 문자와 숫자의 위치에 제한이 없다고 가정한다.
다음 항등식에 대한 조합론적 설명을 제시하시오.

\binom{n}{r}=\binom{n}{n-r}

각 자릿수가 10개의 정수 $0,1, \ldots, 9$ 중 하나인 $n$ 자리 숫자를 고려하시오. 다음을 만족하는 숫자의 수는 몇 가지인가? (a) 연속하는 두 자릿수가 같지 않은 경우: (b) 0이 총 $i$ 번 나타나는 경우, $i=0, \ldots, n$ :
각각 $n$ 명의 학생으로 구성된 세 개의 학급을 고려하시오. 이 3 $n$ 명의 학생 그룹에서 3명의 학생으로 구성된 그룹을 선택해야 한다. (a) 가능한 선택의 수는 몇 가지인가? (b) 3명의 학생 모두 같은 학급에 속하는 선택의 수는 몇 가지인가? (c) 3명의 학생 중 2명은 같은 학급에 속하고 다른 1명은 다른 학급에 속하는 선택의 수는 몇 가지인가? (d) 3명의 학생 모두 다른 학급에 속하는 선택의 수는 몇 가지인가? (e) (a)부터 (d)까지의 결과를 사용하여 조합론적 항등식을 작성하시오.
숫자가 두 번 이상 나타나지 않도록 정수 $1,2, \ldots, 9$ 로 만들 수 있는 5자리 숫자의 수는 몇 가지인가? (예: 41434는 허용되지 않는다.)
10쌍의 부부 중에서 부부가 포함되지 않는 6명의 그룹을 선택하려고 한다. (a) 가능한 선택의 수는 몇 가지인가? (b) 그룹이 반드시 3명의 남자와 3명의 여자로 구성되어야 한다면 가능한 선택의 수는 몇 가지인가?
7명의 남자와 8명의 여자로 구성된 그룹에서 6명의 위원회를 선출해야 한다. 위원회가 적어도 3명의 여자와 적어도 2명의 남자로 구성되어야 한다면, 가능한 서로 다른 위원회의 수는 몇 가지인가? *13. 경매에 나온 미술품 컬렉션은 달리 작품 4점, 반 고흐 작품 5점, 피카소 작품 6점으로 구성되어 있었다. 경매에는 5명의 미술품 수집가가 참여했다. 모든 작품이 판매되었을 때, 기자가 각 수집가가 획득한 달리, 반 고흐, 피카소 작품의 수만 기록했다면, 기록될 수 있는 서로 다른 결과의 수는 몇 가지인가? *14. 각 $x_{i}$ 가 양의 정수이고 다음을 만족하는 벡터 $\left(x_{1}, \ldots, x_{n}\right)$ 의 수를 결정하시오.

\sum_{i=1}^{n} x_{i} \leq k

단, $k \geq n$ 이다. 15. 확률론 보험계리사 시험 대비 강좌에 총 $n$ 명의 학생이 등록했다. 시험 결과는 합격자들의 이름이 점수 내림차순으로 게시될 것이다. 예를 들어, 브라운과 조만이 합격하고 브라운이 더 높은 점수를 받았다면 게시된 결과는 "브라운, 조"가 될 것이다. 모든 점수가 다르다고 가정할 때 (동점 없음), 가능한 게시 결과의 수는 몇 가지인가? 16. 집합 $S=\{1,2, \ldots, 20\}$ 의 크기 4인 부분집합 중 적어도 하나의 원소 $1,2,3,4,5$ 를 포함하는 부분집합의 수는 몇 가지인가? 17. 다음 항등식에 대한 해석적 증명을 제시하시오.

\binom{n}{2}=\binom{k}{2}+k(n-k)+\binom{n-k}{2}, \quad 1 \leq k \leq n

이제 이 항등식에 대한 조합론적 논증을 제시하시오. 18. 특정 지역 사회에는 한부모와 자녀 1명으로 구성된 가족 3가구, 한부모와 자녀 2명으로 구성된 가족 3가구, 부모 2명과 자녀 1명으로 구성된 가족 5가구, 부모 2명과 자녀 2명으로 구성된 가족 7가구, 부모 2명과 자녀 3명으로 구성된 가족 6가구가 있다. 같은 가족의 부모와 자녀를 한 명씩 선택해야 한다면, 가능한 선택의 수는 몇 가지인가? 19. 숫자와 문자의 위치에 제한이 없다면, 5개의 문자와 3개의 숫자로 구성된 8자리 자동차 번호판 중 문자나 숫자의 반복이 허용되지 않는 경우 가능한 번호판의 수는 몇 가지인가? 3개의 숫자가 연속되어야 한다면 몇 가지인가? 20. 다음 등식이

\sum_{x_{1}+\ldots+x_{r}=n, x_{i} \geq 0} \frac{n!}{x_{1}!x_{2}!\cdots x_{r}!}=r^{n}

$n=3, r=2$ 일 때 성립함을 확인하고, 항상 유효함을 보이시오. (합은 합이 $n$ 인 $r$ 개의 음이 아닌 정수 값의 모든 벡터에 대한 것이다.) 힌트: 알파벳의 처음 $r$ 개 문자로 만들 수 있는 서로 다른 $n$ 글자 시퀀스는 몇 가지인가? 그중 각 $i=1, \ldots, r$ 에 대해 알파벳의 $i$ 번째 문자를 총 $x_{i}$ 번 사용하는 시퀀스는 몇 가지인가?

Chapter

Axioms of Probability

2.1 서론 2.2 표본 공간과 사건 2.3 확률의 공리 2.4 몇 가지 간단한 명제 2.5 동일하게 발생할 가능성이 있는 결과를 갖는 표본 공간 2.6 연속 집합 함수로서의 확률 2.7 믿음의 척도로서의 확률

2.1 Introduction

이 장에서는 사건의 확률 개념을 소개하고, 특정 상황에서 확률을 계산하는 방법을 보여준다. 그러나 그에 앞서 표본 공간과 실험의 사건 개념에 대해 논의할 필요가 있다.

2.2 Sample Space and Events

결과를 확실하게 예측할 수 없는 실험을 고려해 보자. 하지만 실험의 결과는 미리 알 수 없지만, 모든 가능한 결과들의 집합은 알려져 있다고 가정해 보자. 실험의 모든 가능한 결과들의 집합을 **표본 공간(sample space)**이라고 하며 $S$ 로 표기한다. 다음은 몇 가지 예시이다:

실험의 결과가 신생아의 성별을 결정하는 것이라면,
$S=\{g, b\}$
여기서 결과 $g$ 는 아이가 여자아이임을 의미하고, $b$ 는 남자아이임을 의미한다.
실험의 결과가 포스트 포지션 $1,2,3,4,5,6,7$ 을 가진 7마리 말의 경주 순서라면,
$S=\{\text { all } 7!\text { permutations of }(1,2,3,4,5,6,7)\}$
예를 들어, 결과 $(2,3,1,6,5,4,7)$ 은 2번 말이 1등, 3번 말이 2등, 1번 말이 3등 등으로 들어왔음을 의미한다.
실험이 두 개의 동전을 던지는 것으로 구성된다면, 표본 공간은 다음 네 가지 점으로 구성된다:
$S=\{(H, H),(H, T),(T, H),(T, T)\}$
두 동전 모두 앞면이면 $(H, H)$ , 첫 번째 동전이 앞면이고 두 번째 동전이 뒷면이면 $(H, T)$ , 첫 번째 동전이 뒷면이고 두 번째 동전이 앞면이면 $(T, H)$ , 두 동전 모두 뒷면이면 $(T, T)$ 가 결과가 된다.
실험이 두 개의 주사위를 던지는 것으로 구성된다면, 표본 공간은 36개의 점으로 구성된다:
$S=\{(i, j): i, j=1,2,3,4,5,6\}$
여기서 $(i, j)$ 결과는 왼쪽 주사위에 $i$ 가 나타나고 다른 주사위에 $j$ 가 나타날 때 발생한다고 말한다.
실험이 트랜지스터의 수명(시간 단위)을 측정하는 것으로 구성된다면, 표본 공간은 모든 음이 아닌 실수로 구성된다; 즉,
$S=\{x: 0 \leq x<\infty\}$

표본 공간의 모든 부분 집합 $E$ 를 **사건(event)**이라고 한다. 다시 말해, 사건은 실험의 가능한 결과들로 구성된 집합이다. 실험의 결과가 $E$ 에 포함되면, 우리는 $E$ 가 발생했다고 말한다. 다음은 사건의 몇 가지 예시이다.

앞의 예시 1에서, 만약 $E=\{g\}$ 라면, $E$ 는 아이가 여자아이인 사건이다. 유사하게, 만약 $F=\{b\}$ 라면, $F$ 는 아이가 남자아이인 사건이다.

예시 2에서, 만약

E=\{\text { all outcomes in } S \text { starting with a } 3\}

이라면, $E$ 는 3번 말이 경주에서 우승하는 사건이다. 예시 3에서, 만약 $E=\{(H, H),(H, T)\}$ 라면, $E$ 는 첫 번째 동전에서 앞면이 나오는 사건이다.

예시 4에서, 만약 $E=\{(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)\}$ 이라면, $E$ 는 주사위의 합이 7이 되는 사건이다.

예시 5에서, 만약 $E=\{x: 0 \leq x \leq 5\}$ 라면, $E$ 는 트랜지스터가 5시간보다 오래 지속되지 않는 사건이다.

표본 공간 $S$ 의 두 사건 $E$ 와 $F$ 에 대해, 우리는 새로운 사건 $E \cup F$ 를 $E$ 에 있거나 $F$ 에 있거나 또는 $E$ 와 $F$ 모두에 있는 모든 결과들로 구성되도록 정의한다. 즉, 사건 $E \cup F$ 는 $E$ 또는 $F$ 중 하나라도 발생하면 발생한다. 예를 들어, 예시 1에서 $E=\{g\}$ 가 아이가 여자아이인 사건이고 $F=\{b\}$ 가 아이가 남자아이인 사건이라면,

E \cup F=\{g, b\}

는 전체 표본 공간 $S$ 이다. 예시 3에서, $E=\{(H, H),(H, T)\}$ 가 첫 번째 동전이 앞면이 나오는 사건이고, $F=\{(T, H),(H, H)\}$ 가 두 번째 동전이 앞면이 나오는 사건이라면,

E \cup F=\{(H, H),(H, T),(T, H)\}

는 적어도 하나의 동전이 앞면이 나오는 사건이며, 따라서 두 동전 모두 뒷면이 나오지 않는 한 발생할 것이다.

사건 $E \cup F$ 를 사건 $E$ 와 사건 $F$ 의 **합집합(union)**이라고 한다. 유사하게, 두 사건 $E$ 와 $F$ 에 대해, 우리는 $E$ 와 $F$ 의 **교집합(intersection)**이라고 불리는 새로운 사건 $E F$ 를 $E$ 와 $F$ 모두에 있는 모든 결과들로 구성되도록 정의할 수 있다. 즉, 사건 $E F$ (때로는 $E \cap F$ 로 쓰기도 한다)는 $E$ 와 $F$ 가 모두 발생할 때만 발생한다. 예를 들어, 예시 3에서 $E=\{(H, H),(H, T),(T, H)\}$ 가 적어도 1개의 앞면이 나오는 사건이고 $F=\{(H, T),(T, H),(T, T)\}$ 가 적어도 1개의 뒷면이 나오는 사건이라면,

E F=\{(H, T),(T, H)\}

는 정확히 1개의 앞면과 1개의 뒷면이 나오는 사건이다. 예시 4에서, $E=\{(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)\}$ 가 주사위의 합이 7인 사건이고 $F=\{(1,5),(2,4),(3,3),(4,2),(5,1)\}$ 가 합이 6인 사건이라면, 사건 $E F$ 는 어떤 결과도 포함하지 않으므로 발생할 수 없다. 이러한 사건에 이름을 부여하기 위해, 우리는 이를 **공사건(null event)**이라고 부르고 $\varnothing$ 로 표기한다. (즉, $\varnothing$ 는 어떤 결과도 포함하지 않는 사건을 의미한다.) 만약 $E F=\varnothing$ 라면, $E$ 와 $F$ 는 **상호 배타적(mutually exclusive)**이라고 말한다.

우리는 두 개 이상의 사건의 합집합과 교집합을 유사한 방식으로 정의한다. 만약 $E_{1}, E_{2}, \ldots$ 가 사건들이라면, 이 사건들의 합집합은 $\bigcup_{n=1}^{\infty} E_{n}$ 으로 표기되며, $n=1,2, \ldots$ 중 적어도 하나의 값에 대해 $E_{n}$ 에 있는 모든 결과들로 구성되는 사건으로 정의된다. 유사하게, 사건 $E_{n}$ 의 교집합은 $\bigcap_{n=1}^{\infty} E_{n}$ 으로 표기되며, 모든 사건 $E_{n}, n=1,2, \ldots$ 에 있는 결과들로 구성되는 사건으로 정의된다.

마지막으로, 모든 사건 $E$ 에 대해, 우리는 $E$ 의 **여사건(complement)**이라고 불리는 새로운 사건 $E^{c}$ 를 표본 공간 $S$ 에서 $E$ 에 포함되지 않는 모든 결과들로 구성되도록 정의한다. 즉, $E^{c}$ 는 $E$ 가 발생하지 않을 때만 발생한다. 예시 4에서, 사건 $E= \{(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)\}$ 이라면, $E^{c}$ 는 주사위의 합이 7이 아닐 때 발생한다. 실험은 반드시 어떤 결과를 가져와야 하므로, $S^{c}=\varnothing$ 가 된다는 점에 유의하라.

두 사건 $E$ 와 $F$ 에 대해, 만약 $E$ 의 모든 결과가 $F$ 에도 포함된다면, 우리는 $E$ 가 $F$ 에 **포함된다(contained in)**고 말하거나 $E$ 가 $F$ 의 **부분 집합(subset)**이라고 말하며 $E \subset F$ (또는 동등하게 $F \supset E$ , 때로는 $F$ 가 $E$ 의 **상위 집합(superset)**이라고 말한다)로 쓴다. 따라서, 만약 $E \subset F$ 라면, $E$ 의 발생은 $F$ 의 발생을 의미한다. 만약 $E \subset F$ 이고 $F \subset E$ 라면, 우리는 $E$ 와 $F$ 가 **같다(equal)**고 말하며 $E=F$ 로 쓴다.

사건들 간의 논리적 관계를 설명하는 데 유용한 그래픽 표현은 **벤 다이어그램(Venn diagram)**이다. 표본 공간 $S$ 는 큰 직사각형 안의 모든 결과들로 구성되는 것으로 표현되며, 사건 $E, F, G, \ldots$ 는 직사각형 안의 주어진 원들 안의 모든 결과들로 구성되는 것으로 표현된다. 관심 있는 사건들은 다이어그램의 적절한 영역을 음영 처리하여 나타낼 수 있다. 예를 들어, 그림 2.1에 표시된 세 개의 벤 다이어그램에서 음영 처리된 영역은 각각 다음 사건들을 나타낸다.

그림 2.1 벤 다이어그램.

그림 2.2 $E \subset F$ .

$E \cup F, E F$ , 그리고 $E^{c}$ 이다. 그림 2.2의 벤 다이어그램은 $E \subset F$ 임을 나타낸다.

사건의 합집합, 교집합, 여집합을 형성하는 연산은 대수학의 규칙과 유사한 특정 규칙을 따른다. 이 규칙 중 몇 가지를 나열한다:

\begin{array}{lcrlrl} \text { 교환 법칙 (Commutative laws)} & E \cup F & =F \cup E & E F & =F E \\ \text { 결합 법칙 (Associative laws)} & (E \cup F) \cup G & =E \cup(F \cup G) & (E F) G & =E(F G) \\ \text { 분배 법칙 (Distributive laws)} & (E \cup F) G & =E G \cup F G & E F \cup G & =(E \cup G)(F \cup G) \end{array}

이러한 관계는 등호의 왼쪽 편에 있는 사건에 포함된 모든 결과가 오른쪽 편에 있는 사건에도 포함되고, 그 반대도 성립함을 보여줌으로써 검증된다. 이를 보여주는 한 가지 방법은 벤 다이어그램을 이용하는 것이다. 예를 들어, 분배 법칙은 그림 2.3의 다이어그램 순서를 통해 검증될 수 있다.

그림 2.3 $(E \cup F) G=E G \cup F G$ .

합집합, 교집합, 여집합을 형성하는 세 가지 기본 연산 간의 다음 유용한 관계는 **드 모르간의 법칙(DeMorgan's laws)**으로 알려져 있다:

\begin{aligned} & \left(\bigcup_{i=1}^{n} E_{i}\right)^{c}=\bigcap_{i=1}^{n} E_{i}^{c} \\ & \left(\bigcap_{i=1}^{n} E_{i}\right)^{c}=\bigcup_{i=1}^{n} E_{i}^{c} \end{aligned}

예를 들어, 두 사건 $E$ 와 $F$ 에 대해 드 모르간의 법칙은 다음과 같이 명시한다:

(E \cup F)^{c}=E^{c} F^{c} \quad \text { and } \quad (E F)^{c}=E^{c} \cup F^{c}

이는 벤 다이어그램을 사용하여 쉽게 증명할 수 있다 (Theoretical Exercise 7 참조). 일반적인 $n$ 에 대한 드 모르간의 법칙을 증명하기 위해, 먼저 $x$ 가 $\left(\bigcup_{i=1}^{n} E_{i}\right)^{c}$ 의 결과라고 가정해 보자. 그러면 $x$ 는 $\bigcup_{i=1}^{n} E_{i}$ 에 포함되지 않으며, 이는 $x$ 가 $E_{i}, i=1,2, \ldots, n$ 중 어떤 사건에도 포함되지 않음을 의미한다. 이는 $x$ 가 모든 $i=1,2, \ldots, n$ 에 대해 $E_{i}^{c}$ 에 포함되고 따라서 $\bigcap_{i=1}^{n} E_{i}^{c}$ 에 포함됨을 의미한다. 반대 방향으로, $x$ 가 $\bigcap_{i=1}^{n} E_{i}^{c}$ 의 결과라고 가정해 보자. 그러면 $x$ 는 모든 $i=1,2, \ldots, n$ 에 대해 $E_{i}^{c}$ 에 포함되며, 이는 $x$ 가 어떤 $i=1,2, \ldots, n$ 에 대해서도 $E_{i}$ 에 포함되지 않음을 의미한다. 이는 $x$ 가 $\bigcup_{i}^{n} E_{i}$ 에 포함되지 않음을 의미하고, 다시 $x$ 가 $\left(\bigcup_{1}^{n} E_{i}\right)^{c}$ 에 포함됨을 의미한다. 이것이 드 모르간의 첫 번째 법칙을 증명한다.

드 모르간의 두 번째 법칙을 증명하기 위해, 우리는 첫 번째 법칙을 사용하여 다음을 얻는다:

\left(\bigcup_{i=1}^{n} E_{i}^{c}\right)^{c}=\bigcap_{i=1}^{n}\left(E_{i}^{c}\right)^{c}

이는 $\left(E^{c}\right)^{c}=E$ 이므로 다음과 동등하다:

\left(\bigcup_{1}^{n} E_{i}^{c}\right)^{c}=\bigcap_{1}^{n} E_{i}

위 방정식의 양변에 여집합을 취하면 우리가 찾던 결과, 즉 다음을 얻는다:

\bigcup_{1}^{n} E_{i}^{c}=\left(\bigcap_{1}^{n} E_{i}\right)^{c}

2.3 Axioms of Probability

어떤 사건의 확률을 정의하는 한 가지 방법은 **상대 빈도(relative frequency)**를 이용하는 것이다. 이러한 정의는 일반적으로 다음과 같다: 표본 공간이 $S$ 인 실험이 정확히 동일한 조건하에서 반복적으로 수행된다고 가정한다. 표본 공간 $S$ 의 각 사건 $E$ 에 대해, 실험의 처음 $n$ 회 반복에서 사건 $E$ 가 발생한 횟수를 $n(E)$ 로 정의한다. 그러면 사건 $E$ 의 확률 $P(E)$ 는 다음과 같이 정의된다.

P(E)=\lim _{n \rightarrow \infty} \frac{n(E)}{n}

즉, $P(E)$ 는 $E$ 가 발생하는 (극한) 시간의 비율로 정의된다. 따라서 이는 $E$ 의 **극한 상대 빈도(limiting relative frequency)**이다.

앞서 언급한 정의는 분명 직관적으로 만족스럽고 독자가 항상 염두에 두어야 하지만, 심각한 단점을 가지고 있다: 우리는 $n(E) / n$ 이 실험의 가능한 각 반복 시퀀스에 대해 동일한 어떤 상수 극한값으로 수렴할 것이라는 것을 어떻게 알 수 있을까? 예를 들어, 반복적으로 수행될 실험이 동전 던지기로 구성된다고 가정해 보자. 처음 $n$ 번의 던지기에서 얻은 앞면의 비율이 $n$ 이 커짐에 따라 어떤 값으로 수렴할 것이라는 것을 어떻게 알 수 있을까? 또한, 어떤 값으로 수렴하더라도, 실험이 두 번째로 반복 수행될 때 동일한 앞면의 극한 비율을 얻을 것이라는 것을 어떻게 알 수 있을까?

확률의 상대 빈도 정의를 지지하는 사람들은 보통 $n(E) / n$ 이 상수 극한값으로 수렴한다는 것이 시스템의 가정, 즉 **공리(axiom)**라고 말함으로써 이러한 반론에 답한다. 그러나 $n(E) / n$ 이 필연적으로 어떤 상수 값으로 수렴할 것이라고 가정하는 것은 비정상적으로 복잡한 가정처럼 보인다. 왜냐하면, 우리는 그러한 상수 극한 빈도가 존재하기를 진정으로 바랄 수 있지만, 이것이 반드시 그래야 한다는 것이 선험적으로(a priori) 명백해 보이지는 않기 때문이다. 사실, 확률에 대한 더 간단하고 자명한 공리 집합을 가정하고, 그런 다음 그러한 상수 극한 빈도가 어떤 의미에서 존재한다는 것을 증명하려고 시도하는 것이 더 합리적이지 않을까? 후자의 접근 방식이 이 책에서 채택할 확률 이론에 대한 현대적인 **공리적 접근 방식(axiomatic approach)**이다. 특히, 우리는 표본 공간 $S$ 의 각 사건 $E$ 에 대해 $E$ 의 확률이라고 불리는 값 $P(E)$ 가 존재한다고 가정할 것이다. 그런 다음 우리는 이 모든 확률이 특정 공리 집합을 만족한다고 가정할 것이며, 독자들도 우리의 직관적인 확률 개념과 일치한다고 동의하기를 바란다.

표본 공간이 $S$ 인 실험을 고려해 보자. 표본 공간 $S$ 의 각 사건 $E$ 에 대해, 숫자 $P(E)$ 가 정의되고 다음 세 가지 공리를 만족한다고 가정한다:

The three axioms of probability

Axiom 1

0 \leq P(E) \leq 1

Axiom 2

P(S)=1

Axiom 3

서로 배타적인 사건 $E_{1}, E_{2}, \ldots$ (즉, $i \neq j$ 일 때 $E_{i} E_{j}=\varnothing$ 인 사건)의 모든 시퀀스에 대해,

P\left(\bigcup_{i=1}^{\infty} E_{i}\right)=\sum_{i=1}^{\infty} P\left(E_{i}\right)

우리는 $P(E)$ 를 사건 $E$ 의 **확률(probability)**이라고 부른다.

따라서 공리 1은 실험의 결과가 $E$ 에 속할 확률이 0과 1 사이의 어떤 숫자임을 명시한다. 공리 2는 확률 1로 결과가 표본 공간 $S$ 의 한 점이 될 것임을 명시한다. 공리 3은 서로 배타적인 사건의 모든 시퀀스에 대해, 이 사건들 중 적어도 하나가 발생할 확률은 각 사건의 확률의 합과 같다고 명시한다.

만약 우리가 사건 $E_{1}, E_{2}, \ldots$ 의 시퀀스를 고려하는데, 여기서 $E_{1}=S$ 이고 $i>1$ 에 대해 $E_{i}=\varnothing$ 이라고 하자. 그러면 이 사건들은 서로 배타적이고 $S=\bigcup_{i=1}^{\infty} E_{i}$ 이므로, 공리 3에 의해 다음을 얻는다.

P(S)=\sum_{i=1}^{\infty} P\left(E_{i}\right)=P(S)+\sum_{i=2}^{\infty} P(\varnothing)

이는 다음을 의미한다.

P(\varnothing)=0

즉, **공사건(null event)**이 발생할 확률은 0이다.
따라서 서로 배타적인 사건 $E_{1}, E_{2}, \ldots, E_{n}$ 의 모든 유한 시퀀스에 대해 다음이 성립한다.

P\left(\bigcup_{1}^{n} E_{i}\right)=\sum_{i=1}^{n} P\left(E_{i}\right)

이 방정식은 $n$ 보다 큰 모든 $i$ 값에 대해 $E_{i}$ 를 공사건으로 정의함으로써 공리 3으로부터 도출된다. 표본 공간이 유한할 때 공리 3은 방정식 (3.1)과 동등하다. (왜 그럴까?) 그러나 표본 공간이 무한한 수의 점으로 구성될 때 공리 3의 추가적인 일반성은 필수적이다.

Example 3a

만약 동전을 던지는 실험을 하고 앞면이 나올 확률과 뒷면이 나올 확률이 같다고 가정하면, 다음과 같이 표현할 수 있다.

P(\{H\})=P(\{T\})=\frac{1}{2}

반면에, 만약 동전이 편향되어 앞면이 뒷면보다 두 배 더 많이 나올 것이라고 믿는다면, 다음과 같이 표현할 수 있다.

P(\{H\})=\frac{2}{3} \quad P(\{T\})=\frac{1}{3}

예시 3b

주사위를 굴리고 여섯 면이 모두 동일하게 나올 가능성이 있다고 가정하면, $P(\{1\})=P(\{2\})=P(\{3\})=P(\{4\})=P(\{5\})=P(\{6\})=\frac{1}{6}$ 이 된다. 따라서 Axiom 3에 따라 짝수가 나올 확률은 다음과 같다.

P(\{2,4,6\})=P(\{2\})+P(\{4\})+P(\{6\})=\frac{1}{2}

표본 공간 $S$ 의 사건(event)에 대해 정의되고 Axiom 1, 2, 3을 만족하는 집합 함수 $P$ 의 존재를 가정하는 것이 확률 이론에 대한 현대 수학적 접근 방식이다. 독자들은 이 공리들이 자연스럽고 우연과 무작위성과 관련된 확률에 대한 우리의 직관적인 개념과 일치한다는 점에 동의할 것이라고 생각한다. 더욱이, 이 공리들을 사용하여 우리는 실험이 계속해서 반복될 때, 확률 1로 특정 사건 $E$ 가 발생하는 시간의 비율이 $P(E)$ 와 같아질 것임을 증명할 수 있다. **강대수의 법칙(strong law of large numbers)**으로 알려진 이 결과는 8장에서 제시된다. 또한, 2.7절에서는 확률에 대한 또 다른 가능한 해석인 **'믿음의 척도(measure of belief)'**로서의 확률을 제시한다.

기술적 설명. 우리는 $P(E)$ 가 표본 공간의 모든 사건 $E$ 에 대해 정의된다고 가정했다. 실제로 표본 공간이 **비가산 무한 집합(uncountably infinite set)**일 때, $P(E)$ 는 **가측(measurable)**이라고 불리는 사건들의 클래스에 대해서만 정의된다. 그러나 실제 관심 있는 모든 사건은 가측이므로 이 제한에 대해 걱정할 필요는 없다.

2.4 Some Simple Propositions

이 섹션에서는 확률에 관한 몇 가지 간단한 명제를 증명한다. 먼저 $E$ 와 $E^{c}$ 는 항상 상호 배타적이고 $E \cup E^{c}=S$ 이므로, 공리 2와 3에 의해 다음이 성립한다.

1=P(S)=P\left(E \cup E^{c}\right)=P(E)+P\left(E^{c}\right)

또는 이와 동등하게 명제 4.1이 성립한다.

Proposition

4.1

P\left(E^{c}\right)=1-P(E)

Proposition 4.1은 어떤 사건이 발생하지 않을 확률은 그 사건이 발생할 확률을 1에서 뺀 값과 같다고 말한다. 예를 들어, 동전을 던져 앞면이 나올 확률이 $\frac{3}{8}$ 이라면, 뒷면이 나올 확률은 $\frac{5}{8}$ 이어야 한다.

두 번째 명제는 사건 $E$ 가 사건 $F$ 에 포함되면 $E$ 의 확률은 $F$ 의 확률보다 크지 않다는 것이다.

Proposition 4.2

증명 $E \subset F$ 이므로, $F$ 를 다음과 같이 표현할 수 있다.

F=E \cup E^{c} F

따라서 $E$ 와 $E^{c} F$ 는 **상호 배타적(mutually exclusive)**이므로, Axiom 3에 따라 다음을 얻는다.

P(F)=P(E)+P\left(E^{c} F\right)

이는 $P\left(E^{c} F\right) \geq 0$ 이므로 결과를 증명한다.

Proposition 4.2는 예를 들어, 주사위를 굴려 1이 나올 확률은 주사위를 굴려 홀수가 나올 확률보다 작거나 같다는 것을 알려준다.

다음 명제는 두 사건의 합집합(union) 확률과 각 사건의 개별 확률, 그리고 사건들의 교집합(intersection) 확률 사이의 관계를 제시한다.

Proposition

4.3

P(E \cup F)=P(E)+P(F)-P(E F)

증명 $P(E \cup F)$ 에 대한 공식을 도출하기 위해, 먼저 $E \cup F$ 가 두 개의 서로소 사건 $E$ 와 $E^{c} F$ 의 합집합으로 작성될 수 있음을 주목한다. 따라서 공리 3으로부터 다음을 얻는다.

\begin{aligned} P(E \cup F) & =P\left(E \cup E^{c} F\right) \\ & =P(E)+P\left(E^{c} F\right) \end{aligned}

Figure 2.4 벤 다이어그램.

Figure 2.5 섹션으로 나눈 벤 다이어그램.

더 나아가, $F=E F \cup E^{c} F$ 이므로, 공리 3으로부터 다시 다음을 얻는다.

P(F)=P(E F)+P\left(E^{c} F\right)

또는 동등하게,

P\left(E^{c} F\right)=P(F)-P(E F)

이로써 증명이 완료된다. $\square$

명제 4.3은 Figure 2.4의 벤 다이어그램을 사용하여 증명할 수도 있다.

Figure 2.5에 표시된 것처럼 $E \cup F$ 를 세 개의 상호 배타적인 섹션으로 나누어 보자. 즉, 섹션 I은 $F$ 에 속하지 않는 $E$ 의 모든 점(즉, $E F^{c}$ ), 섹션 II는 $E$ 와 $F$ 모두에 속하는 모든 점(즉, $E F$ ), 섹션 III은 $E$ 에 속하지 않는 $F$ 의 모든 점(즉, $E^{c} F$ )을 나타낸다.

Figure 2.5에서 다음을 알 수 있다.

\begin{aligned} E \cup F & =\mathrm{I} \cup \mathrm{II} \cup \mathrm{III} \\ E & =\mathrm{I} \cup \mathrm{II} \\ F & =\mathrm{II} \cup \mathrm{III} \end{aligned}

I, II, III은 상호 배타적이므로, 공리 3으로부터 다음이 성립한다.

\begin{aligned} P(E \cup F) & =P(\mathrm{I})+P(\mathrm{II})+P(\mathrm{III}) \\ P(E) & =P(\mathrm{I})+P(\mathrm{II}) \\ P(F) & =P(\mathrm{II})+P(\mathrm{III}) \end{aligned}

이는 다음을 보여준다.

P(E \cup F)=P(E)+P(F)-P(\mathrm{II})

그리고 $\mathrm{II}=E F$ 이므로 명제 4.3이 증명된다.

예제 4a

J는 휴가에 두 권의 책을 가져간다. 첫 번째 책을 좋아할 확률은 .5이고, 두 번째 책을 좋아할 확률은 .4이며, 두 책 모두를 좋아할 확률은 .3이다. 그녀가 두 책 모두를 좋아하지 않을 확률은 얼마인가?

풀이 J가 책 $i$ 를 좋아하는 사건을 $B_{i}, i=1,2$ 라고 하자. 그러면 그녀가 적어도 한 권의 책을 좋아할 확률은 다음과 같다.

P\left(B_{1} \cup B_{2}\right)=P\left(B_{1}\right)+P\left(B_{2}\right)-P\left(B_{1} B_{2}\right)=.5+.4-.3=.6

J가 두 책 모두를 좋아하지 않는 사건은 그녀가 적어도 한 권의 책을 좋아하는 사건의 여사건이므로, 다음 결과를 얻는다.

P\left(B_{1}^{c} B_{2}^{c}\right)=P\left(\left(B_{1} \cup B_{2}\right)^{c}\right)=1-P\left(B_{1} \cup B_{2}\right)=.4

또한 세 사건 $E, F, G$ 중 어느 하나가 발생할 확률, 즉 다음을 계산할 수 있다.

P(E \cup F \cup G)=P[(E \cup F) \cup G]

이는 명제 4.3에 의해 다음과 같다.

P(E \cup F)+P(G)-P[(E \cup F) G]

이제 분배 법칙에 따라 사건 $(E \cup F) G$ 와 $E G \cup F G$ 는 동등하다. 따라서 이전 방정식으로부터 다음을 얻는다.

\begin{aligned} & P(E \cup F \cup G) \\ & \quad=P(E)+P(F)-P(E F)+P(G)-P(E G \cup F G) \\ & \quad=P(E)+P(F)-P(E F)+P(G)-P(E G)-P(F G)+P(E G F G) \\ & \quad=P(E)+P(F)+P(G)-P(E F)-P(E G)-P(F G)+P(E F G) \end{aligned}

사실, **포함-배제 원리(inclusion-exclusion identity)**로 알려진 다음 명제는 수학적 귀납법으로 증명될 수 있다.

명제 4.4

\begin{aligned} P\left(E_{1} \cup E_{2} \cup \cdots \cup E_{n}\right)= & \sum_{i=1}^{n} P\left(E_{i}\right)-\sum_{i_{1}<i_{2}} P\left(E_{i_{1}} E_{i_{2}}\right)+\cdots \\ & +(-1)^{r+1} \sum_{i_{1}<i_{2}<\cdots<i_{r}} P\left(E_{i_{1}} E_{i_{2}} \cdots E_{i_{r}}\right) \\ & +\cdots+(-1)^{n+1} P\left(E_{1} E_{2} \cdots E_{n}\right) \end{aligned}

합계 $\sum_{i_{1}<i_{2}<\cdots<i_{r}} P\left(E_{i_{1}} E_{i_{2}} \cdots E_{i_{r}}\right)$ 는 집합 $\{1,2, \ldots, n\}$ 의 크기 $r$ 인 가능한 $\binom{n}{r}$ 개의 모든 부분집합에 대해 계산된다.

명제 4.4는 $n$ 개 사건의 합집합의 확률은 이들 사건의 확률을 한 번에 하나씩 더한 값에서, 두 개씩 더한 확률을 뺀 다음, 세 개씩 더한 확률을 더하는 식으로 계속된다는 것을 의미한다.

비고 1. 명제 4.4에 대한 비귀납적 논증을 위해, 먼저 표본 공간의 결과가 어떤 집합 $E_{i}$ 의 원소도 아니라면, 그 확률은 등식의 양쪽에 아무런 기여도 하지 않는다는 점에 주목한다. 이제, 어떤 결과가 정확히 $m$ 개의 사건 $E_{i}$ 에 속한다고 가정하자( $m>0$ ). 그러면 이 결과는 $\bigcup_{i} E_{i}$ 에 속하므로 $P\left(\bigcup_{i} E_{i}\right)$ 에서 한 번 계산된다. 또한, 이 결과는 $E_{i_{1}} E_{i_{2}} \cdots E_{i_{k}}$ 유형의 $\binom{m}{k}$ 개 부분집합에 포함되므로, 명제 4.4의 등호 오른쪽에 다음 횟수만큼 계산된다.

\binom{m}{1}-\binom{m}{2}+\binom{m}{3}-\cdots \pm\binom{ m}{m}

따라서 $m>0$ 일 때 다음을 보여야 한다.

1=\binom{m}{1}-\binom{m}{2}+\binom{m}{3}-\cdots \pm\binom{ m}{m}

그러나 $1=\binom{m}{0}$ 이므로, 위 방정식은 다음 식과 동등하다.

\sum_{i=0}^{m}\binom{m}{i}(-1)^{i}=0

그리고 후자의 방정식은 이항 정리에 의해 다음으로부터 도출된다.

0=(-1+1)^{m}=\sum_{i=0}^{m}\binom{m}{i}(-1)^{i}(1)^{m-i}

다음은 포함-배제 원리를 간결하게 작성하는 방법이다.

P\left(\cup_{i=1}^{n} E_{i}\right)=\sum_{r=1}^{n}(-1)^{r+1} \sum_{i_{1}<\cdots<i_{r}} P\left(E_{i_{1}} \cdots E_{i_{r}}\right)

포함-배제 원리에서, 한 항까지 계산하면 합집합의 확률에 대한 **상한(upper bound)**이 되고, 두 항까지 계산하면 확률에 대한 **하한(lower bound)**이 되며, 세 항까지 계산하면 확률에 대한 상한이 되고, 네 항까지 계산하면 하한이 되는 식으로 계속된다. 즉, 사건 $E_{1}, \ldots, E_{n}$ 에 대해 다음이 성립한다.

\begin{aligned} & P\left(\cup_{i=1}^{n} E_{i}\right) \leq \sum_{i=1}^{n} P\left(E_{i}\right) \\ & P\left(\cup_{i=1}^{n} E_{i}\right) \geq \sum_{i=1}^{n} P\left(E_{i}\right)-\sum_{j<i} P\left(E_{i} E_{j}\right) \\ & P\left(\cup_{i=1}^{n} E_{i}\right) \leq \sum_{i=1}^{n} P\left(E_{i}\right)-\sum_{j<i} P\left(E_{i} E_{j}\right)+\sum_{k<j<i} P\left(E_{i} E_{j} E_{k}\right) \end{aligned}

등등. 이러한 경계의 유효성을 증명하기 위해 다음 항등식에 주목한다.

\cup_{i=1}^{n} E_{i}=E_{1} \cup E_{1}^{c} E_{2} \cup E_{1}^{c} E_{2}^{c} E_{3} \cup \cdots \cup E_{1}^{c} \cdots E_{n-1}^{c} E_{n}

즉, $E_{1}$ 이 발생하거나, $E_{1}$ 이 발생하지 않지만 $E_{2}$ 가 발생하거나, $E_{1}$ 과 $E_{2}$ 가 발생하지 않지만 $E_{3}$ 가 발생하는 등, 적어도 하나의 사건 $E_{i}$ 가 발생한다. 우변은 서로소 사건들의 합집합이므로 다음을 얻는다.

\begin{aligned} P\left(\cup_{i=1}^{n} E_{i}\right) & =P\left(E_{1}\right)+P\left(E_{1}^{c} E_{2}\right)+P\left(E_{1}^{c} E_{2}^{c} E_{3}\right)+\ldots+P\left(E_{1}^{c} \cdots E_{n-1}^{c} E_{n}\right) \\ & =P\left(E_{1}\right)+\sum_{i=2}^{n} P\left(E_{1}^{c} \cdots E_{i-1}^{c} E_{i}\right) \end{aligned}

이제 $B_{i}=E_{1}^{c} \cdots E_{i-1}^{c}=\left(\cup_{j<i} E_{j}\right)^{c}$ 를 처음 $i-1$ 개 사건 중 어느 것도 발생하지 않는 사건이라고 하자. 항등식

P\left(E_{i}\right)=P\left(B_{i} E_{i}\right)+P\left(B_{i}^{c} E_{i}\right)

를 적용하면 다음을 알 수 있다.

P\left(E_{i}\right)=P\left(E_{1}^{c} \cdots E_{i-1}^{c} E_{i}\right)+P\left(E_{i} \cup_{j<i} E_{j}\right)

또는 동등하게,

P\left(E_{1}^{c} \cdots E_{i-1}^{c} E_{i}\right)=P\left(E_{i}\right)-P\left(\cup_{j<i} E_{i} E_{j}\right)

이 방정식을 (4.4)에 대입하면 다음이 나온다.

P\left(\cup_{i=1}^{n} E_{i}\right)=\sum_{i} P\left(E_{i}\right)-\sum_{i} P\left(\cup_{j<i} E_{i} E_{j}\right)

확률은 항상 음이 아니므로, 부등식 (4.1)은 방정식 (4.5)로부터 직접적으로 도출된다. 이제 $i$ 를 고정하고 $P\left(\cup_{j<i} E_{i} E_{j}\right)$ 에 부등식 (4.1)을 적용하면 다음이 나온다.

P\left(\cup_{j<i} E_{i} E_{j}\right) \leq \sum_{j<i} P\left(E_{i} E_{j}\right)

이는 방정식 (4.5)에 의해 부등식 (4.2)를 제공한다. 유사하게, $i$ 를 고정하고 $P\left(\cup_{j<i} E_{i} E_{j}\right)$ 에 부등식 (4.2)를 적용하면 다음이 나온다.

\begin{aligned} P\left(\cup_{j<i} E_{i} E_{j}\right) & \geq \sum_{j<i} P\left(E_{i} E_{j}\right)-\sum_{k<j<i} P\left(E_{i} E_{j} E_{i} E_{k}\right) \\ & =\sum_{j<i} P\left(E_{i} E_{j}\right)-\sum_{k<j<i} P\left(E_{i} E_{j} E_{k}\right) \end{aligned}

이는 방정식 (4.5)에 의해 부등식 (4.3)을 제공한다. 다음 포함-배제 부등식은 이제 $i$ 를 고정하고 $P\left(\cup_{j<i} E_{i} E_{j}\right)$ 에 부등식 (4.3)을 적용하는 식으로 계속해서 얻어진다.

2.5 Sample Spaces Having Equally Likely Outcomes

많은 실험에서 표본 공간(sample space)의 모든 결과가 발생할 확률이 동일하다고 가정하는 것이 자연스럽다. 즉, 표본 공간 $S$ 가 유한 집합인 실험을 고려해보자. 예를 들어, $S=\{1,2, \ldots, N\}$ 이라고 하자. 이때 다음과 같이 가정하는 것이 자연스러운 경우가 많다.

P(\{1\})=P(\{2\})=\cdots=P(\{N\})

이는 공리 2와 3에 의해 (왜 그런지는 생각해보자) 다음을 의미한다.

P(\{i\})=\frac{1}{N} \quad i=1,2, \ldots, N

이 방정식으로부터 공리 3에 따라 임의의 사건 $E$ 에 대해 다음이 성립한다.

P(E)=\frac{\text { number of outcomes in } E}{\text { number of outcomes in } S}

다시 말해, 실험의 모든 결과가 발생할 확률이 동일하다고 가정하면, 임의의 사건 $E$ 의 확률은 표본 공간에 포함된 결과 중 $E$ 에 포함되는 결과의 비율과 같다.

Example 5a

Example 5b

두 개의 주사위를 굴릴 때, 윗면의 합이 7이 될 확률은 얼마인가?

해법 우리는 36가지 가능한 모든 결과가 동일하게 발생할 가능성이 있다고 가정하고 이 문제를 해결할 것이다. 주사위의 합이 7이 되는 결과는 $(1,6)$ , $(2,5)$ , $(3,4)$ , $(4,3)$ , $(5,2)$ , $(6,1)$ 의 6가지이므로, 원하는 확률은 $\frac{6}{36}=\frac{1}{6}$ 이다.

6개의 흰 공과 5개의 검은 공이 들어 있는 그릇에서 3개의 공을 "무작위로 뽑을" 때, 한 공은 흰색이고 다른 두 공은 검은색일 확률은 얼마인가?

해법 공들을 구별할 수 있고 선택 순서가 관련 있다고 간주하면, 표본 공간은 $11 \cdot 10 \cdot 9=990$ 가지 결과로 구성된다. 또한, 첫 번째 공이 흰색이고 나머지 두 공이 검은색인 경우는 $6 \cdot 5 \cdot 4=120$ 가지 결과가 있다. 첫 번째 공이 검은색이고 두 번째 공이 흰색이며 세 번째 공이 검은색인 경우는 $5 \cdot 6 \cdot 4=120$ 가지 결과가 있고, 처음 두 공이 검은색이고 세 번째 공이 흰색인 경우는 $5 \cdot 4 \cdot 6=120$ 가지 결과가 있다. 따라서 "무작위로 뽑는다"는 것이 표본 공간의 각 결과가 동일하게 발생할 가능성이 있다는 것을 의미한다고 가정하면, 원하는 확률은 다음과 같다.

\frac{120+120+120}{990}=\frac{4}{11}

이 문제는 실험의 결과를 뽑힌 공들의 순서 없는 집합으로 간주하여 해결할 수도 있었다. 이 관점에서 보면, 표본 공간에는 $\binom{11}{3}=165$ 가지 결과가 있다. 이제 3개의 공으로 이루어진 각 집합은 선택 순서를 고려할 때 3!가지 결과에 해당한다. 결과적으로, 선택 순서를 고려할 때 모든 결과가 동일하게 발생할 가능성이 있다고 가정하면, 선택된 공들의 순서 없는 집합으로 결과를 간주할 때도 동일하게 발생할 가능성이 있다. 따라서 실험의 후자 표현을 사용하면, 원하는 확률은 다음과 같다.

\frac{\binom{6}{1}\binom{5}{2}}{\binom{11}{3}}=\frac{4}{11}

이는 물론 이전에 얻은 답과 일치한다. 실험이 $n$ 개의 항목으로 구성된 집합에서 $k$ 개의 항목을 무작위로 선택하는 경우, 우리는 실험의 결과를 $k$ 개의 항목의 순서 있는 선택으로 하거나, 선택된 항목들의 순서 없는 집합으로 할 수 있는 유연성을 갖는다. 전자의 경우, 각 새로운 선택이 집합의 아직 선택되지 않은 항목 중 어느 것이든 동일하게 발생할 가능성이 있다고 가정하고, 후자의 경우, $k$ 개의 항목으로 구성된 모든 $\binom{n}{k}$ 가지 가능한 부분집합이 선택된 집합이 될 가능성이 동일하다고 가정한다. 예를 들어, 10쌍의 부부로 구성된 20명의 개인 그룹에서 5명을 무작위로 선택해야 하고, 선택된 5명이 모두 무관할 확률 $P(N)$ 을 결정하고 싶다고 가정해 보자. (즉, 두 사람이 서로 결혼한 관계가 아니다.) 표본 공간을 선택된 5명의 사람들의 집합으로 간주하면, $\binom{20}{5}$ 가지 동일하게 발생할 가능성이 있는 결과가 있다. 결혼한 커플을 포함하지 않는 결과는 6단계 실험의 결과로 생각할 수 있다: 첫 번째 단계에서는 그룹에 포함될 10쌍의 커플 중 5쌍을 선택한다. 다음 5단계에서는 이들 각 커플의 2명의 구성원 중 1명을 선택한다. 따라서 선택된 5명의 구성원이 무관한 가능한 결과는 $\binom{10}{5} 2^{5}$ 가지이며, 원하는 확률은 다음과 같다.

P(N)=\frac{\binom{10}{5} 2^{5}}{\binom{20}{5}}

대조적으로, 실험의 결과를 5명의 개인의 순서 있는 선택으로 할 수도 있다. 이 설정에서는 $20 \cdot 19 \cdot 18 \cdot 17 \cdot 16$ 가지 동일하게 발생할 가능성이 있는 결과가 있으며, 이 중 $20 \cdot 18 \cdot 16 \cdot 14 \cdot 12$ 가지 결과는 5명의 무관한 개인 그룹을 초래하여 다음 결과를 얻는다.

P(N)=\frac{20 \cdot 18 \cdot 16 \cdot 14 \cdot 12}{20 \cdot 19 \cdot 18 \cdot 17 \cdot 16}

두 답이 동일하다는 것을 독자가 확인하도록 남겨둔다.

예제 5c

6명의 남성과 9명의 여성으로 구성된 그룹에서 5명의 위원회를 선출한다. 무작위로 선출할 경우, 위원회가 남성 3명과 여성 2명으로 구성될 확률은 얼마인가? 해법 가능한 $\binom{15}{5}$ 가지 위원회 각각이 동일하게 선택될 가능성이 있으므로, 원하는 확률은 다음과 같다.

\frac{\binom{6}{3}\binom{9}{2}}{\binom{15}{5}}=\frac{240}{1001}

예제 5d

항아리에 $n$ 개의 공이 들어 있는데, 그 중 하나는 특별한 공이다. 이 공들 중 $k$ 개를 한 번에 하나씩 뽑는데, 각 선택 시 남아 있는 공 중 어느 것이든 동일하게 뽑힐 가능성이 있다면, 특별한 공이 선택될 확률은 얼마인가?

해법 모든 공이 동일하게 취급되므로, 선택된 $k$ 개의 공 집합은 $k$ 개의 공으로 이루어진 $\binom{n}{k}$ 가지 집합 중 어느 것이든 동일하게 발생할 가능성이 있다. 따라서,

P\{\text { 특별한 공이 선택됨 }\}=\frac{\binom{1}{1}\binom{n-1}{k-1}}{\binom{n}{k}}=\frac{k}{n}

이 결과는 특별한 공이 $i$ 번째로 선택될 사건을 $A_{i}$ 로 나타냄으로써 얻을 수도 있었다 ( $i=1, \ldots, k$ ). 그러면 $n$ 개의 공 각각이 $i$ 번째로 선택될 가능성이 동일하므로 $P\left(A_{i}\right)=1 / n$ 이다. 따라서 이 사건들은 분명히 상호 배타적이므로, 우리는 다음을 얻는다.

P\{\text { 특별한 공이 선택됨 }\}=P\left(\bigcup_{i=1}^{k} A_{i}\right)=\sum_{i=1}^{k} P\left(A_{i}\right)=\frac{k}{n}

또한, 실험의 $n(n-1) \cdots (n-k+1)=n!/(n-k)!$ 가지 동일하게 발생할 가능성이 있는 결과 중 $(n-1)(n-2) \cdots(n-i+1)(1)(n-i) \cdots(n-k+1)=(n-1)!/(n-k)!$ 가지 결과가 특별한 공이 $i$ 번째로 선택되는 결과를 초래한다는 점을 주목하여 $P\left(A_{i}\right)=1 / n$ 이라고 주장할 수도 있었다. 이러한 추론에 따르면,

P\left(A_{i}\right)=\frac{(n-1)!}{n!}=\frac{1}{n}

예제 5e

$n$ 개의 빨간 공과 $m$ 개의 파란 공으로 구성된 $n+m$ 개의 공이 선형 순서로 배열되어 있으며, 가능한 모든 $(n+m)$ !가지 순서가 동일하게 발생할 가능성이 있다고 가정하자. 이 실험의 결과를 연속적인 공들의 색상만 나열하여 기록할 때, 가능한 모든 결과가 동일하게 발생할 가능성이 있음을 보여라.

해법 가능한 $(n+m)$ !가지 순서 중 하나를 고려하고, 빨간 공들 사이의 순열과 파란 공들 사이의 순열은 색상 시퀀스를 변경하지 않는다는 점에 주목하자. 결과적으로, 색상의 모든 순서는 $n!m!$ 가지 다른 $n+m$ 개의 공의 순서에 해당하므로, 색상의 모든 순서는 발생할 확률이 $\frac{n!m!}{(n+m)!}$ 이다.

예를 들어, 번호가 매겨진 2개의 빨간 공 $r_{1}, r_{2}$ 와 번호가 매겨진 2개의 파란 공 $b_{1}, b_{2}$ 가 있다고 가정하자. 그러면 가능한 $4!$ 가지 순서 중, 특정 색상 조합을 초래하는 순서는 $2!2!$ 가지가 있을 것이다. 예를 들어, 다음 순서들은 빨간 공이 먼저 오고 연속적인 공들이 색상이 번갈아 나타나는 결과를 초래한다.

r_{1}, b_{1}, r_{2}, b_{2} \quad r_{1}, b_{2}, r_{2}, b_{1} \quad r_{2}, b_{1}, r_{1}, b_{2} \quad r_{2}, b_{2}, r_{1}, b_{1}

따라서 색상의 가능한 각 순서는 발생할 확률이 $\frac{4}{24}=\frac{1}{6}$ 이다.

Example 5f

포커 핸드는 5장의 카드로 구성된다. 만약 카드의 숫자가 연속적이고 모두 같은 무늬가 아니라면, 우리는 그 핸드를 **스트레이트(straight)**라고 부른다. 예를 들어, 스페이드 5, 스페이드 6, 스페이드 7, 스페이드 8, 하트 9로 구성된 핸드는 스트레이트이다. 스트레이트를 받을 확률은 얼마인가?

풀이 우리는 가능한 모든 $\binom{52}{5}$ 개의 포커 핸드가 동일하게 나올 확률을 가정한다. 스트레이트가 되는 결과의 수를 결정하기 위해, 먼저 포커 핸드가 에이스, 2, 3, 4, 5로 구성되는 가능한 결과의 수를 결정하자(무늬는 무관하다). 에이스는 가능한 4개의 에이스 중 1개일 수 있고, 2, 3, 4, 5도 마찬가지이므로, 정확히 에이스, 2, 3, 4, 5가 나오는 결과는 $4^{5}$ 개이다. 이 중 4개의 결과에서는 모든 카드가 같은 무늬일 것이므로(이러한 핸드를 **스트레이트 플러시(straight flush)**라고 한다), 에이스, 2, 3, 4, 5 형태의 스트레이트를 구성하는 핸드는 $4^{5}-4$ 개이다. 마찬가지로, 10, J, Q, K, A 형태의 스트레이트를 구성하는 핸드도 $4^{5}-4$ 개이다. 따라서 스트레이트인 핸드는 $10\left(4^{5}-4\right)$ 개이며, 원하는 확률은 다음과 같다.

\frac{10\left(4^{5}-4\right)}{\binom{52}{5}} \approx .0039

예제 5g

5장의 포커 핸드가 **풀 하우스(full house)**라고 하는 것은 같은 숫자의 카드 3장과 다른 숫자의 같은 카드 2장으로 구성될 때이다(물론, 첫 번째 숫자와는 다르다). 따라서 풀 하우스는 **트리플(three of a kind)**과 **페어(pair)**의 조합이다. 풀 하우스를 받을 확률은 얼마인가?

풀이 다시, 우리는 가능한 모든 $\binom{52}{5}$ 개의 핸드가 동일하게 나올 확률을 가정한다. 가능한 풀 하우스의 수를 결정하기 위해, 먼저 예를 들어 2장의 10과 3장의 J의 경우 $\binom{4}{2}\binom{4}{3}$ 개의 다른 조합이 있다는 점에 주목한다. 페어의 종류에 대해 13가지의 다른 선택지가 있고, 페어가 선택된 후 나머지 3장의 카드 숫자에 대해 12가지의 다른 선택지가 있으므로, 풀 하우스의 확률은 다음과 같다.

\frac{13 \cdot 12 \cdot\binom{4}{2}\binom{4}{3}}{\binom{52}{5}} \approx .0014

예제 5h

브리지 게임에서 52장의 카드 덱 전체가 4명의 플레이어에게 분배된다. 다음 확률은 얼마인가? (a) 한 플레이어가 13장의 스페이드를 모두 받는 경우 (b) 각 플레이어가 에이스 1장씩을 받는 경우

풀이 (a) 핸드 $i$ 가 13장의 스페이드를 모두 받는 사건을 $E_{i}$ 라고 하면,

P\left(E_{i}\right)=\frac{1}{\binom{52}{13}}, \quad i=1,2,3,4

사건 $E_{i}, i=1,2,3,4$ 는 **상호 배타적(mutually exclusive)**이므로, 한 핸드가 13장의 스페이드를 모두 받을 확률은 다음과 같다.

P\left(\cup_{i=1}^{4} E_{i}\right)=\sum_{i=1}^{4} P\left(E_{i}\right)=4 /\binom{52}{13} \approx 6.3 \times 10^{-12}

(b) 각기 다른 플레이어가 정확히 에이스 1장씩을 받는 결과의 수를 결정하기 위해, 에이스를 따로 두고 나머지 48장의 카드를 각 플레이어가 12장씩 받도록 나누는 가능한 방법은 $\binom{48}{12,12,12,12}$ 개임을 주목한다. 4장의 에이스를 각 플레이어가 1장씩 받도록 나누는 방법은 4!가지이므로, 각 플레이어가 정확히 에이스 1장씩을 받는 가능한 결과의 수는 $4!\binom{48}{12,12,12,12}$ 개이다.

가능한 핸드는 $\binom{52}{13,13,13,13}$ 개이므로, 원하는 확률은 다음과 같다.

\frac{4!\binom{48}{12,12,12,12}}{\binom{52}{13,13,13,13}} \approx .1055

확률의 일부 결과는 처음 접했을 때 상당히 놀랍다. 다음 두 예제는 이러한 현상을 보여준다.

Example 5i

만약 $n$ 명의 사람이 방에 있다면, 그들 중 어느 두 명도 같은 날에 생일을 맞이하지 않을 확률은 얼마인가? 이 확률이 $\frac{1}{2}$ 보다 작아지려면 $n$ 은 얼마나 커야 하는가?

풀이: 각 사람은 365일 중 어느 하루에 생일을 맞이할 수 있으므로, 총 $(365)^{n}$ 가지의 가능한 결과가 있다. (2월 29일에 태어난 사람의 가능성은 무시한다.) 각 결과가 동일하게 발생할 가능성이 있다고 가정하면, 원하는 확률은 $(365)(364)(363) \ldots(365-n+1) /(365)^{n}$ 이다.

놀랍게도 $n \geq 23$ 일 때 이 확률은 $\frac{1}{2}$ 보다 작다. 즉, 방에 23명 이상의 사람이 있다면, 적어도 두 명이 같은 생일을 가질 확률은 $\frac{1}{2}$ 을 초과한다. 많은 사람들은 이 결과에 처음에는 놀라는데, 23이라는 숫자가 연간 일수인 365에 비해 너무 작게 느껴지기 때문이다. 그러나 모든 개인 쌍은 $\frac{365}{(365)^{2}}=\frac{1}{365}$ 의 확률로 같은 생일을 가지며, 23명의 그룹에는 $\binom{23}{2}=253$ 개의 서로 다른 개인 쌍이 존재한다. 이러한 관점에서 보면, 이 결과는 더 이상 그렇게 놀랍지 않다.

방에 50명이 있을 때, 적어도 두 명이 같은 생일을 공유할 확률은 약 0.970이며, 방에 100명이 있을 때는 확률이 3,000,000:1보다 높다. (즉, 적어도 두 사람이 같은 생일을 가질 확률은 $\frac{3 \times 10^{6}}{3 \times 10^{6}+1}$ 보다 크다.)

Example <br> 5j

52장의 트럼프 카드를 섞은 후, 첫 번째 에이스가 나올 때까지 한 장씩 뒤집는다. 첫 번째 에이스 다음 카드, 즉 첫 번째 에이스 바로 뒤에 나오는 카드가 스페이드 에이스일 가능성이 높을까, 아니면 클럽 2일 가능성이 높을까?

풀이: 첫 번째 에이스 다음 카드가 스페이드 에이스일 확률을 결정하기 위해, 우리는 52장의 카드를 배열하는 가능한 (52)!가지 순서 중 스페이드 에이스가 첫 번째 에이스 바로 뒤에 오는 순서가 몇 가지인지 계산해야 한다.
우선, 52장의 카드를 배열하는 각 순서는 스페이드 에이스를 제외한 51장의 카드를 먼저 배열한 다음, 그 배열에 스페이드 에이스를 삽입하여 얻을 수 있다는 점에 주목하자. 또한, 다른 카드 51장의 (51)!가지 배열 각각에 대해, 스페이드 에이스가 첫 번째 에이스 뒤에 오도록 삽입될 수 있는 위치는 단 한 곳뿐이다. 예를 들어, 다른 51장의 카드 배열이 다음과 같다고 가정해보자.

4 c, 6 h, J d, 5 s, A c, 7 d, \ldots, K h

이 배열에 스페이드 에이스를 삽입하여 첫 번째 에이스 뒤에 오도록 하는 유일한 방법은 다음과 같다.

4 c, 6 h, J d, 5 s, A c, A s, 7 d, \ldots, K h

따라서 스페이드 에이스가 첫 번째 에이스 뒤에 오는 배열은 (51)!가지이므로,

P\{\text { the ace of spades follows the first ace }\}=\frac{(51)!}{(52)!}=\frac{1}{52}

사실, 정확히 동일한 논리에 따라 클럽 2(또는 다른 특정 카드)가 첫 번째 에이스 뒤에 올 확률도 $\frac{1}{52}$ 이다. 다시 말해, 덱의 52장 카드 각각은 첫 번째 에이스 뒤에 올 가능성이 동일하다!

많은 사람들이 이 결과에 상당히 놀라워한다. 실제로 흔한 반응은 처음에는 클럽 2가 (스페이드 에이스보다) 첫 번째 에이스 뒤에 올 가능성이 더 높다고 생각하는 것이다. 왜냐하면 첫 번째 에이스 자체가 스페이드 에이스일 수도 있기 때문이다. 이러한 반응은 종종 클럽 2 자체가 첫 번째 에이스보다 먼저 나타날 수 있어서, 첫 번째 에이스 바로 뒤에 올 기회를 상실할 수 있다는 깨달음으로 이어진다. 그러나 스페이드 에이스가 첫 번째 에이스가 될 확률은 4분의 1이고(4개의 에이스 모두 첫 번째가 될 가능성이 동일하므로), 클럽 2가 첫 번째 에이스보다 먼저 나타날 확률은 5분의 1에 불과하기 때문에(클럽 2와 4개의 에이스로 구성된 5장의 카드 세트 중 각 카드가 이 세트에서 첫 번째로 나타날 가능성이 동일하므로), 다시 클럽 2가 더 가능성이 높아 보인다. 하지만 이것은 사실이 아니며, 우리의 더 완전한 분석은 두 가지 가능성이 동일하다는 것을 보여준다.

Example

한 축구팀은 20명의 공격수와 20명의 수비수로 구성된다. 이 선수들을 룸메이트를 정하기 위해 2명씩 짝지으려고 한다. 무작위로 짝을 지을 때, 공격수-수비수 룸메이트 쌍이 없을 확률은 얼마인가? $2i$ 개의 공격수-수비수 룸메이트 쌍이 있을 확률은 얼마인가? ( $i=1,2, \ldots, 10$ )

풀이: 40명의 선수를 각각 2명씩 20개의 순서 있는 쌍으로 나누는 방법의 수는 다음과 같다:

\binom{40}{2,2, \ldots, 2}=\frac{(40)!}{(2!)^{20}}

(즉, 선수를 첫 번째 쌍, 두 번째 쌍 등으로 나누는 방법의 수는 $(40)! / 2^{20}$ 이다.) 따라서 선수를 2명씩 (순서 없는) 쌍으로 나누는 방법의 수는 $(40)! / 2^{20}(20)!$ 이다.

더 나아가, 공격수(및 수비수)들이 자기들끼리만 짝을 이룰 경우 공격수-수비수 쌍이 전혀 생기지 않으므로, 이러한 분할의 수는 $\left[(20)!/ 2^{10}(10)!\right]^{2}$ 이다. 따라서 공격수-수비수 룸메이트 쌍이 없을 확률을 $P_{0}$ 라고 하면, $P_{0}$ 는 다음과 같이 주어진다:

P_{0}=\frac{\left(\frac{(20)!}{2^{10}(10)!}\right)^{2}}{\frac{(40)!}{2^{20}(20)!}}=\frac{[(20)!]^{3}}{[(10)!]^{2}(40)!}

$2i$ 개의 공격수-수비수 쌍이 있을 확률인 $P_{2i}$ 를 구하기 위해, 먼저 공격수-수비수 쌍에 포함될 $2i$ 명의 공격수와 $2i$ 명의 수비수를 선택하는 방법의 수가 $\binom{20}{2i}^{2}$ 임을 주목한다. 이 $4i$ 명의 선수들은 $(2i)!$ 가지 가능한 공격수-수비수 쌍으로 짝지어질 수 있다. (이는 첫 번째 공격수가 $2i$ 명의 수비수 중 누구와도 짝을 이룰 수 있고, 두 번째 공격수는 남은 $2i-1$ 명의 수비수 중 누구와도 짝을 이룰 수 있는 식으로 계속되기 때문이다.)

남은 $20-2i$ 명의 공격수(및 수비수)들은 자기들끼리 짝을 이루어야 하므로, $2i$ 개의 공격수-수비수 쌍을 만드는 분할의 수는 다음과 같다:

\binom{20}{2i}^{2}(2i)!\left[\frac{(20-2i)!}{2^{10-i}(10-i)!}\right]^{2}

따라서,

P_{2i}=\frac{\binom{20}{2i}^{2}(2i)!\left[\frac{(20-2i)!}{2^{10-i}(10-i)!}\right]^{2}}{\frac{(40)!}{2^{20}(20)!}} \quad i=0,1, \ldots, 10

$P_{2i}, i=0,1, \ldots, 10$ 는 이제 계산될 수 있으며, Stirling의 근사식( $n! \approx n^{n+1/2} e^{-n} \sqrt{2 \pi}$ )을 사용하여 근사치를 구할 수도 있다. 예를 들어, 우리는 다음을 얻는다:

\begin{aligned} & P_{0} \approx 1.3403 \times 10^{-6} \\ & P_{10} \approx .345861 \\ & P_{20} \approx 7.6068 \times 10^{-6} \end{aligned}

$\square$

다음 세 가지 예시는 **포함-배제 원리(Proposition 4.4)**의 유용성을 보여준다. 예제 51에서는 확률의 도입을 통해 계산 문제에 대한 빠른 해결책을 얻을 수 있다.

Example 51

어떤 클럽의 회원 중 36명은 테니스를 치고, 28명은 스쿼시를 치며, 18명은 배드민턴을 친다. 또한, 22명은 테니스와 스쿼시를 모두 치고, 12명은 테니스와 배드민턴을 모두 치며, 9명은 스쿼시와 배드민턴을 모두 치고, 4명은 세 가지 스포츠를 모두 친다. 이 클럽 회원 중 적어도 한 가지 스포츠를 하는 회원은 몇 명인가?

풀이 클럽 회원 수를 $N$ 이라고 하고, 클럽 회원이 무작위로 선택된다고 가정하여 확률을 도입한다. 클럽 회원의 어떤 부분집합 $C$ 에 대해, 선택된 회원이 $C$ 에 포함될 확률을 $P(C)$ 라고 하면,

P(C)=\frac{\text { number of members in } C}{N}

이제 테니스를 치는 회원들의 집합을 $T$ , 스쿼시를 치는 회원들의 집합을 $S$ , 배드민턴을 치는 회원들의 집합을 $B$ 라고 하면, 명제 4.4에 따라 다음을 얻는다.

\begin{aligned} P(T \cup S \cup & B) \\ & =P(T)+P(S)+P(B)-P(T S)-P(T B)-P(S B)+P(T S B) \\ & =\frac{36+28+18-22-12-9+4}{N} \\ & =\frac{43}{N} \end{aligned}

따라서 43명의 회원이 적어도 한 가지 스포츠를 한다고 결론 내릴 수 있다. $\square$

이 섹션의 다음 예시는 다소 놀라운 답을 제시할 뿐만 아니라 이론적으로도 흥미롭다.

Example <br> 5m

The matching problem

파티에 참석한 $N$ 명의 남자가 각자의 모자를 방 중앙에 던진다. 모자들은 먼저 섞인 다음, 각 남자가 무작위로 모자를 하나씩 선택한다. 이들 중 어느 누구도 자신의 모자를 선택하지 않을 확률은 얼마인가?

풀이 우리는 먼저 적어도 한 명의 남자가 자신의 모자를 선택할 **여사건(complementary probability)**을 계산한다. $i$ 번째 남자가 자신의 모자를 선택하는 사건을 $E_i, i=1, 2, \ldots, N$ 이라고 하자. 이제 **명제 4.4(Proposition 4.4)**에 따라, 적어도 한 명의 남자가 자신의 모자를 선택할 확률 $P\left(\bigcup_{i=1}^{N} E_{i}\right)$ 는 다음과 같이 주어진다.

\begin{aligned} P\left(\bigcup_{i=1}^{N} E_{i}\right)= & \sum_{i=1}^{N} P\left(E_{i}\right)-\sum_{i_{1}<i_{2}} P\left(E_{i_{1}} E_{i_{2}}\right)+\cdots \\ & +(-1)^{n+1} \sum_{i_{1}<i_{2} \cdots<i_{n}} P\left(E_{i_{1}} E_{i_{2}} \cdots E_{i_{n}}\right) \\ & +\cdots+(-1)^{N+1} P\left(E_{1} E_{2} \cdots E_{N}\right) \end{aligned}

이 실험의 결과를 $N$ 개의 숫자로 이루어진 벡터로 간주하면, $i$ 번째 요소는 $i$ 번째 남자가 뽑은 모자의 번호가 된다. 이때 가능한 결과는 $N!$ 가지이다. (예를 들어, $(1,2,3, \ldots, N)$ 이라는 결과는 각 남자가 자신의 모자를 선택했음을 의미한다.)
더 나아가, $n$ 명의 남자 $i_1, i_2, \ldots, i_n$ 각각이 자신의 모자를 선택하는 사건인 $E_{i_1} E_{i_2} \ldots E_{i_n}$ 은 $(N-n)(N-n-1) \cdots 3 \cdot 2 \cdot 1=(N-n)!$ 가지 방식으로 발생할 수 있다. 왜냐하면, 나머지 $N-n$ 명의 남자 중 첫 번째 남자는 $N-n$ 개의 모자 중 아무거나 선택할 수 있고, 두 번째 남자는 $N-n-1$ 개의 모자 중 아무거나 선택할 수 있으며, 이런 식으로 계속되기 때문이다.
따라서 모든 $N!$ 가지 가능한 결과가 동일하게 발생할 확률을 가정하면, 다음을 알 수 있다.

P\left(E_{i_{1}} E_{i_{2}} \cdots E_{i_{n}}\right)=\frac{(N-n)!}{N!}

또한, $\sum_{i_{1}<i_{2} \cdots<i_{n}} P\left(E_{i_{1}} E_{i_{2}} \cdots E_{i_{n}}\right)$ 에는 $\binom{N}{n}$ 개의 항이 있으므로, 다음이 성립한다.

\sum_{i_{1}<i_{2} \cdots<i_{n}} P\left(E_{i_{1}} E_{i_{2}} \cdots E_{i_{n}}\right)=\frac{N!(N-n)!}{(N-n)!n!N!}=\frac{1}{n!}

그러므로,

P\left(\bigcup_{i=1}^{N} E_{i}\right)=1-\frac{1}{2!}+\frac{1}{3!}-\cdots+(-1)^{N+1} \frac{1}{N!}

따라서, 어느 누구도 자신의 모자를 선택하지 않을 확률은 다음과 같다.

1-1+\frac{1}{2!}-\frac{1}{3!}+\ldots+\frac{(-1)^{N}}{N!}=\sum_{i=0}^{N}(-1)^{i} / i!

항등식 $e^{x}=\sum_{i=0}^{\infty} x^{i} / i!$ 에 $x=-1$ 을 대입하면, $N$ 이 클 때 위 확률은 대략 $e^{-1} \approx .3679$ 와 같음을 알 수 있다. 다시 말해, $N$ 이 클 때, 어느 누구도 자신의 모자를 선택하지 않을 확률은 대략 .37이다. (얼마나 많은 독자들이 이 확률이 $N \rightarrow \infty$ 일 때 1로 수렴할 것이라고 잘못 생각했을까?)

**명제 4.4(Proposition 4.4)**의 유용성을 보여주는 또 다른 예시로 다음을 고려해보자.

예제 5n

10쌍의 부부가 원형 테이블에 무작위로 앉을 때, 어떤 아내도 남편 옆에 앉지 않을 확률을 계산하시오.

풀이 $i$ 번째 부부가 서로 옆에 앉는 사건을 $E_i, i=1,2, \ldots, 10$ 이라고 하면, 우리가 구하고자 하는 확률은 $1-P\left(\bigcup_{i=1}^{10} E_{i}\right)$ 이다. 이제 **명제 4.4(Proposition 4.4)**에 따르면,

\begin{aligned} P\left(\bigcup_{1}^{10} E_{i}\right)= & \sum_{1}^{10} P\left(E_{i}\right)-\cdots+(-1)^{n+1} \sum_{i_{1}<i_{2}<\cdots<i_{n}} P\left(E_{i_{1}} E_{i_{2}} \cdots E_{i_{n}}\right) \\ & +\cdots-P\left(E_{1} E_{2} \cdots E_{10}\right) \end{aligned}

$P\left(E_{i_{1}} E_{i_{2}} \cdots E_{i_{n}}\right)$ 을 계산하기 위해, 먼저 20명의 사람을 원형 테이블에 배열하는 방법이 19!가지라는 점에 주목한다. (왜 그럴까?)
특정 $n$ 쌍의 부부가 서로 옆에 앉는 배열의 수는 각 $n$ 쌍의 부부를 단일 개체로 생각하는 것이 가장 쉽다. 이 경우, 우리는 $20-n$ 개의 개체를 원형 테이블에 배열해야 하며, 이러한 배열은 분명히 $(20-n-1)!$ 가지이다. 마지막으로, 각 $n$ 쌍의 부부는 서로 옆에 앉는 두 가지 가능한 방식으로 배열될 수 있으므로, 특정 $n$ 쌍의 부부가 각각 자신의 배우자 옆에 앉는 배열은 $2^{n}(20-n-1)!$ 가지이다.
따라서,

P\left(E_{i_{1}} E_{i_{2}} \cdots E_{i_{n}}\right)=\frac{2^{n}(19-n)!}{(19)!}

그러므로 **명제 4.4(Proposition 4.4)**로부터, 적어도 한 쌍의 부부가 함께 앉을 확률은 다음과 같다.

$\binom{10}{1} 2^{1} \frac{(18)!}{(19)!}-\binom{10}{2} 2^{2} \frac{(17)!}{(19)!}+\binom{10}{3} 2^{3} \frac{(16)!}{(19)!}-\cdots-\binom{10}{10} 2^{10} \frac{9!}{(19)!} \approx .6605$

그리고 우리가 구하고자 하는 확률은 대략 .3395이다.

*Example <br> 50

Runs

$n$ 승 $m$ 패의 최종 기록으로 시즌을 마친 운동팀을 생각해 보자. 승패의 순서를 조사하여, 팀이 다른 시기보다 이길 가능성이 더 높은 경기 구간을 가졌는지 여부를 파악하고자 한다. 이 질문에 대한 통찰력을 얻는 한 가지 방법은 승리 run의 수를 세어보고, $n$ 승과 $m$ 패의 모든 $(n+m)!/(n!m!)$ 순서가 동일하게 발생할 가능성이 있다고 가정할 때 그 결과가 얼마나 가능성이 있는지 확인하는 것이다. 승리 run이란 연속된 승리 시퀀스를 의미한다. 예를 들어, $n=10, m=6$ 이고 결과 시퀀스가 $W W L L W W W L W L L L W W W W$ 였다면, 4개의 승리 run이 있었을 것이다. 첫 번째 run은 크기 2, 두 번째는 크기 3, 세 번째는 크기 1, 네 번째는 크기 4이다.

이제 한 팀이 $n$ 승과 $m$ 패를 기록했다고 가정해 보자. 모든 $(n+m)!/(n!m!)=\binom{n+m}{n}$ 순서가 동일하게 발생할 가능성이 있다고 가정할 때, 정확히 $r$ 개의 승리 run이 있을 확률을 결정해 보자. 이를 위해 먼저 $x_{1}+\cdots+x_{r}=n$ 을 만족하는 양의 정수 벡터 $x_{1}, x_{2}, \ldots, x_{r}$ 를 고려하고, $i$ 번째 run의 크기가 $x_{i}, i=1, \ldots, r$ 인 $r$ 개의 승리 run을 초래하는 결과가 몇 개인지 살펴보자. 이러한 모든 결과에 대해, 첫 번째 승리 run 이전에 발생한 패배의 수를 $y_{1}$ , 첫 번째와 두 번째 승리 run 사이에 발생한 패배의 수를 $y_{2}, \ldots$ , 마지막 승리 run 이후에 발생한 패배의 수를 $y_{r+1}$ 이라고 하면, $y_{i}$ 는 다음을 만족한다.

y_{1}+y_{2}+\cdots+y_{r+1}=m \quad y_{1} \geq 0, y_{r+1} \geq 0, y_{i}>0, i=2, \ldots, r

그리고 결과는 다음과 같이 도식적으로 표현될 수 있다.

\underbrace{L L \ldots L}_{y_{1}} \underbrace{W W \ldots W}_{x_{1}} \underbrace{L \ldots L}_{y_{2}} \underbrace{W W \ldots W}_{x_{2}} \cdots \underbrace{W W}_{x_{r}} \underbrace{L \ldots L}_{y_{r+1}}

따라서 $r$ 개의 승리 run(각 $i$ 번째 run의 크기는 $x_{i}, i=1, \ldots r$ )을 초래하는 결과의 수는 위 조건을 만족하는 정수 $y_{1}, \ldots, y_{r+1}$ 의 수와 같으며, 이는 다음을 만족하는 양의 정수

\bar{y}_{1}=y_{1}+1 \quad \bar{y}_{i}=y_{i}, i=2, \ldots, r, \bar{y}_{r+1}=y_{r+1}+1

의 수와 동일하다.

\bar{y}_{1}+\bar{y}_{2}+\cdots+\bar{y}_{r+1}=m+2

1장의 명제 6.1에 따르면, 이러한 결과는 $\binom{m+1}{r}$ 개이다. 따라서 $r$ 개의 승리 run을 초래하는 총 결과의 수는 $\binom{m+1}{r}$ 에 $x_{1}+\cdots+x_{r}=n$ 의 양의 정수 해의 수를 곱한 값이다. 따라서 다시 명제 6.1에 따라, $r$ 개의 승리 run을 초래하는 결과는 $\binom{m+1}{r}\binom{n-1}{r-1}$ 개이다. $\binom{n+m}{n}$ 개의 동일하게 발생할 가능성이 있는 결과가 있으므로, 다음이 성립한다.

P(\{r \text { runs of wins }\})=\frac{\binom{m+1}{r}\binom{n-1}{r-1}}{\binom{m+n}{n}} \quad r \geq 1

예를 들어, $n=8$ 이고 $m=6$ 인 경우, 모든 $\binom{14}{8}$ 개의 결과가 동일하게 발생할 가능성이 있다면 7개의 run이 발생할 확률은 $\binom{7}{7}\binom{7}{6} / \binom{14}{8}=1 / 429$ 이다. 따라서 결과가 $W L W L W L W L W W L W L W$ 였다면, 우리는 팀의 승리 확률이 시간이 지남에 따라 변하고 있다고 의심할 수 있다. (특히, 팀이 마지막 경기를 졌을 때 이길 확률은 상당히 높고, 마지막 경기를 이겼을 때 이길 확률은 상당히 낮은 것으로 보인다.) 반대 극단으로, 결과가 $W W W W W W W W L L L L L L$ 였다면, run은 1개뿐이었을 것이고, $P(\{1 \operatorname{run}\})=\binom{7}{1}\binom{7}{0} /\binom{14}{8}= 1 / 429$ 이므로, 팀의 승리 확률이 14경기 동안 변하지 않았다고 보기는 다시 어려울 것이다.

*2.6 Probability as a Continuous Set Function

사건의 시퀀스 $\left\{E_{n}, n \geq 1\right\}$ 는 다음과 같으면 **증가 시퀀스(increasing sequence)**라고 한다:

E_{1} \subset E_{2} \subset \cdots \subset E_{n} \subset E_{n+1} \subset \cdots

반면에 다음과 같으면 **감소 시퀀스(decreasing sequence)**라고 한다:

E_{1} \supset E_{2} \supset \cdots \supset E_{n} \supset E_{n+1} \supset \cdots

만약 $\left\{E_{n}, n \geq 1\right\}$ 이 사건의 증가 시퀀스라면, 우리는 $\lim _{n \rightarrow \infty} E_{n}$ 으로 표기되는 새로운 사건을 다음과 같이 정의한다:

\lim _{n \rightarrow \infty} E_{n}=\bigcup_{i=1}^{\infty} E_{i}

마찬가지로, 만약 $\left\{E_{n}, n \geq 1\right\}$ 이 사건의 감소 시퀀스라면, 우리는 $\lim _{n \rightarrow \infty} E_{n}$ 을 다음과 같이 정의한다:

\lim _{n \rightarrow \infty} E_{n}=\bigcap_{i=1}^{\infty} E_{i}

이제 다음 명제 6.1을 증명한다:

명제 만약 $\left\{E_{n}, n \geq 1\right\}$ 이 사건의 증가 시퀀스이거나 감소 시퀀스라면, 6.1

\lim _{n \rightarrow \infty} P\left(E_{n}\right)=P\left(\lim _{n \rightarrow \infty} E_{n}\right)

증명 먼저, $\left\{E_{n}, n \geq 1\right\}$ 이 증가 시퀀스라고 가정하고, 사건 $F_{n}, n \geq 1$ 을 다음과 같이 정의한다:

\begin{aligned} & F_{1}=E_{1} \\ & F_{n}=E_{n}\left(\bigcup_{1}^{n-1} E_{i}\right)^{c}=E_{n} E_{n-1}^{c} \quad n>1 \end{aligned}

여기서 사건들이 증가 시퀀스이므로 $\bigcup_{1}^{n-1} E_{i}=E_{n-1}$ 이라는 사실을 사용했다. 즉, $F_{n}$ 은 $E_{n}$ 에 속하지만 이전의 어떤 $E_{i}, i<n$ 에도 속하지 않는 결과들로 구성된다. $F_{n}$ 이 다음과 같은 **상호 배타적인 사건(mutually exclusive events)**임을 쉽게 확인할 수 있다:

\bigcup_{i=1}^{\infty} F_{i}=\bigcup_{i=1}^{\infty} E_{i} \quad \text { and } \quad \bigcup_{i=1}^{n} F_{i}=\bigcup_{i=1}^{n} E_{i} \quad \text { for all } n \geq 1

따라서,

\begin{aligned} P\left(\bigcup_{1}^{\infty} E_{i}\right) & =P\left(\bigcup_{1}^{\infty} F_{i}\right) \\ & =\sum_{1}^{\infty} P\left(F_{i}\right) \quad(\text { Axiom 3에 의해) } \\ & =\lim _{n \rightarrow \infty} \sum_{1}^{n} P\left(F_{i}\right) \\ & =\lim _{n \rightarrow \infty} P\left(\bigcup_{1}^{n} F_{i}\right) \\ & =\lim _{n \rightarrow \infty} P\left(\bigcup_{1}^{n} E_{i}\right) \\ & =\lim _{n \rightarrow \infty} P\left(E_{n}\right) \end{aligned}

이는 $\left\{E_{n}, n \geq 1\right\}$ 이 증가 시퀀스일 때의 결과를 증명한다. 만약 $\left\{E_{n}, n \geq 1\right\}$ 이 감소 시퀀스라면, $\left\{E_{n}^{c}, n \geq 1\right\}$ 은 증가 시퀀스이다. 따라서 앞선 방정식들로부터,

P\left(\bigcup_{1}^{\infty} E_{i}^{c}\right)=\lim _{n \rightarrow \infty} P\left(E_{n}^{c}\right)

그러나 $\bigcup_{1}^{\infty} E_{i}^{c}=\left(\bigcap_{1}^{\infty} E_{i}\right)^{c}$ 이므로, 다음이 성립한다:

P\left(\left(\bigcap_{1}^{\infty} E_{i}\right)^{c}\right)=\lim _{n \rightarrow \infty} P\left(E_{n}^{c}\right)

또는 동등하게,

1-P\left(\bigcap_{1}^{\infty} E_{i}\right)=\lim _{n \rightarrow \infty}\left[1-P\left(E_{n}\right)\right]=1-\lim _{n \rightarrow \infty} P\left(E_{n}\right)

또는

P\left(\bigcap_{1}^{\infty} E_{i}\right)=\lim _{n \rightarrow \infty} P\left(E_{n}\right)

이는 결과를 증명한다.

Example 6a

Probability and a "paradox"

무한히 큰 항아리와 1번, 2번, 3번 등 번호가 매겨진 무한한 공 컬렉션이 있다고 가정해 보자. 다음과 같이 수행되는 실험을 고려해 보자: 정오 1분 전, 1번부터 10번까지의 공이 항아리에 넣어지고 10번 공이 꺼내진다. (꺼내는 데 시간이 걸리지 않는다고 가정한다.) 정오 $\frac{1}{2}$ 분 전, 11번부터 20번까지의 공이 항아리에 넣어지고 20번 공이 꺼내진다. 정오 $\frac{1}{4}$ 분 전, 21번부터 30번까지의 공이 항아리에 넣어지고 30번 공이 꺼내진다. 정오 $\frac{1}{8}$ 분 전, 이런 식으로 계속된다. 관심 있는 질문은 정오에 항아리 안에 몇 개의 공이 있는가? 이다.

이 질문에 대한 답은 분명히 정오에 항아리 안에 무한한 수의 공이 있다는 것이다. 왜냐하면 $10n$ ( $n \geq 1$ ) 형태가 아닌 번호의 공은 모두 항아리에 넣어지고 정오 이전에 꺼내지지 않을 것이기 때문이다. 따라서 실험이 설명된 대로 수행될 때 문제는 해결된다.

그러나 이제 실험을 변경하여 정오 1분 전, 1번부터 10번까지의 공이 항아리에 넣어지고 1번 공이 꺼내진다고 가정해 보자. 정오 $\frac{1}{2}$ 분 전, 11번부터 20번까지의 공이 항아리에 넣어지고 2번 공이 꺼내진다. 정오 $\frac{1}{4}$ 분 전, 21번부터 30번까지의 공이 항아리에 넣어지고 3번 공이 꺼내진다. 정오 $\frac{1}{8}$ 분 전, 31번부터 40번까지의 공이 항아리에 넣어지고 4번 공이 꺼내지는 식으로 계속된다. 이 새로운 실험에서 정오에 항아리 안에 몇 개의 공이 있는가?

놀랍게도, 이제 답은 정오에 항아리가 비어 있다는 것이다. 어떤 공이든, 예를 들어 $n$ 번 공을 생각해 보자. 정오 이전의 어느 시점(특히 정오 $\left(\frac{1}{2}\right)^{n-1}$ 분 전)에 이 공은 항아리에서 꺼내졌을 것이다. 따라서 각 $n$ 에 대해 $n$ 번 공은 정오에 항아리 안에 없다. 그러므로 그 시점에 항아리는 비어 있어야 한다.

모든 $n$ 에 대해 $n$ 번째 교환 후 항아리 안의 공의 수는 두 가지 실험 변형 모두에서 동일하기 때문에, 대부분의 사람들은 두 시나리오가 극한에서 이렇게 다른 결과를 낳는다는 것에 놀란다. 결과가 다른 이유는 실제 역설이나 수학적 모순 때문이 아니라 상황의 논리 때문이며, 또한 무한을 다룰 때의 초기 직관이 항상 옳지 않기 때문에 놀라운 결과가 나온다는 것을 인식하는 것이 중요하다. (이 후자의 진술은 놀라운 일이 아니다. 19세기 후반에 수학자 게오르크 칸토어(Georg Cantor)가 무한 이론을 처음 개발했을 때, 당시 다른 주요 수학자들 중 많은 이들이 이를 무의미하다고 비난하고, 모든 정수의 집합과 모든 짝수 정수의 집합이 같은 수의 원소를 가진다는 주장 때문에 칸토어를 조롱했기 때문이다.)

앞선 논의에서 공이 꺼내지는 방식이 차이를 만든다는 것을 알 수 있다. 첫 번째 경우, $n \geq 1$ 인 $10n$ 번 공만 꺼내지는 반면, 두 번째 경우에는 모든 공이 결국 꺼내진다. 이제 공을 꺼낼 때마다 현재 있는 공 중에서 무작위로 선택된다고 가정해 보자. 즉, 정오 1분 전, 1번부터 10번까지의 공이 항아리에 넣어지고 공이 무작위로 선택되어 꺼내지는 식으로 계속된다고 가정해 보자. 이 경우, 정오에 항아리 안에 몇 개의 공이 있는가?

풀이 우리는 확률 1로 정오에 항아리가 비어 있을 것임을 보일 것이다. 먼저 1번 공을 고려해 보자. $E_n$ 을 첫 $n$ 번의 공을 꺼낸 후에도 1번 공이 여전히 항아리에 남아 있는 사건이라고 정의하자. 분명히,

P\left(E_{n}\right)=\frac{9 \cdot 18 \cdot 27 \cdots(9 n)}{10 \cdot 19 \cdot 28 \cdots(9 n+1)}

[이 방정식을 이해하려면, 1번 공이 첫 $n$ 번의 공을 꺼낸 후에도 항아리에 남아 있으려면, 첫 번째로 꺼내지는 공은 9개 중 하나일 수 있고, 두 번째로 꺼내지는 공은 18개 중 하나일 수 있다는 점에 주목하면 된다 (두 번째 공을 꺼낼 때 항아리에는 19개의 공이 있으며, 그 중 하나는 1번 공이어야 한다). 분모도 유사하게 얻어진다.]

이제 정오에 1번 공이 항아리에 있는 사건은 $\bigcap_{n=1}^{\infty} E_{n}$ 사건이다. 사건 $E_n, n \geq 1$ 은 감소하는 사건이므로, 명제 6.1에 따라 다음이 성립한다. $P\{$ 정오에 1번 공이 항아리에 있다 $\}$

\begin{aligned} & =P\left(\bigcap_{n=1}^{\infty} E_{n}\right) \\ & =\lim _{n \rightarrow \infty} P\left(E_{n}\right) \\ & =\prod_{n=1}^{\infty}\left(\frac{9 n}{9 n+1}\right) \end{aligned}

이제 우리는 다음을 보일 것이다.

\prod_{n=1}^{\infty} \frac{9 n}{9 n+1}=0

왜냐하면

\prod_{n=1}^{\infty}\left(\frac{9 n}{9 n+1}\right)=\left[\prod_{n=1}^{\infty}\left(\frac{9 n+1}{9 n}\right)\right]^{-1}

이므로, 이는 다음을 보이는 것과 동등하다.

\prod_{n=1}^{\infty}\left(1+\frac{1}{9 n}\right)=\infty

이제 모든 $m \geq 1$ 에 대해,

\begin{aligned} \prod_{n=1}^{\infty}\left(1+\frac{1}{9 n}\right) & \geq \prod_{n=1}^{m}\left(1+\frac{1}{9 n}\right) \\ & =\left(1+\frac{1}{9}\right)\left(1+\frac{1}{18}\right)\left(1+\frac{1}{27}\right) \cdots\left(1+\frac{1}{9 m}\right) \\ & >\frac{1}{9}+\frac{1}{18}+\frac{1}{27}+\cdots+\frac{1}{9 m} \\ & =\frac{1}{9} \sum_{i=1}^{m} \frac{1}{i} \end{aligned}

따라서 $m \rightarrow \infty$ 로 보내고 $\sum_{i=1}^{\infty} 1 / i=\infty$ 라는 사실을 사용하면 다음을 얻는다.

\prod_{n=1}^{\infty}\left(1+\frac{1}{9 n}\right)=\infty

그러므로 $F_i$ 를 정오에 $i$ 번 공이 항아리에 있는 사건이라고 하면, 우리는 $P\left(F_{1}\right)=0$ 임을 보였다. 유사하게, 모든 $i$ 에 대해 $P\left(F_{i}\right)=0$ 임을 보일 수 있다. (예를 들어, 동일한 추론으로 $i=11, 12, \ldots, 20$ 에 대해 $P\left(F_{i}\right)=\prod_{n=2}^{\infty}[9 n /(9 n+1)]$ 임을 알 수 있다.) 따라서 정오에 항아리가 비어 있지 않을 확률 $P\left(\bigcup_{1}^{\infty} F_{i}\right)$ 는 다음을 만족한다.

P\left(\bigcup_{1}^{\infty} F_{i}\right) \leq \sum_{1}^{\infty} P\left(F_{i}\right)=0

이는 **부등식(Boole's inequality)**에 따른 것이다. (자체 평가 연습 14 참조.) 따라서 확률 1로 정오에 항아리는 비어 있을 것이다.

2.7 Probability as a Measure of Belief

지금까지 우리는 주어진 실험의 어떤 사건에 대한 확률을 실험이 계속 반복될 때 그 사건이 얼마나 자주 발생할 것인지에 대한 척도로 해석해 왔다. 그러나 확률이라는 용어에는 다른 용례도 있다. 예를 들어, 우리는 "셰익스피어가 실제로 햄릿을 썼을 확률은 90%이다" 또는 "오스왈드가 케네디 암살에서 단독으로 행동했을 확률은 0.8이다"와 같은 진술을 모두 들어본 적이 있다. 이러한 진술을 어떻게 해석해야 할까?

가장 간단하고 자연스러운 해석은 언급된 확률이 진술하는 사람의 진술에 대한 믿음의 정도를 측정하는 척도라는 것이다. 다시 말해, 앞서 언급한 진술을 하는 사람은 오스왈드가 단독으로 행동했다고 상당히 확신하며, 셰익스피어가 햄릿을 썼다고 훨씬 더 확신한다. 확률을 개인의 믿음의 정도를 측정하는 척도로 해석하는 이러한 방식은 종종 개인적(personal) 또는 주관적(subjective) 확률 관점이라고 불린다.

"개인의 믿음의 정도를 측정하는 척도"가 확률의 모든 공리를 만족해야 한다고 가정하는 것이 논리적으로 보인다. 예를 들어, 셰익스피어가 줄리어스 시저를 썼다고 70% 확신하고, 실제로 말로우가 썼다고 10% 확신한다면, 셰익스피어 또는 말로우 둘 중 한 명이 썼다고 80% 확신하는 것이 논리적이라고 가정할 수 있다. 따라서 확률을 믿음의 척도로 해석하든 장기적인 발생 빈도로 해석하든, 그 수학적 특성은 변하지 않는다.

Example

7마리의 말이 경주하는 상황에서, 당신은 처음 2마리의 말이 각각 20%의 우승 확률을 가지고 있고, 3번과 4번 말은 각각 15%의 확률을 가지며, 나머지 3마리의 말은 각각 10%의 확률을 가진다고 믿는다고 가정해 보자. 우승마가 처음 세 마리 중 하나일 것이라는 데 짝수 배당으로 내기를 거는 것이 나을까, 아니면 우승마가 1, 5, 6, 7번 말 중 하나일 것이라는 데 다시 짝수 배당으로 내기를 거는 것이 나을까?

풀이 경주 결과에 대한 당신의 개인적인 확률에 따르면, 첫 번째 내기에서 이길 확률은 $.2+.2+.15=.55$ 이고, 두 번째 내기에서 이길 확률은 $.2+.1+.1+.1=.5$ 이다. 따라서 첫 번째 내기가 더 매력적이다.

사람의 주관적 확률이 항상 확률의 공리와 일치한다고 가정하는 것은 실제 사람이 아닌 이상적인 사람을 다루는 것임을 주목해야 한다. 예를 들어, 만약 우리가 어떤 사람에게 다음 질문에 대한 확률이 얼마라고 생각하는지 묻는다면: (a) 오늘 비가 올 확률, (b) 내일 비가 올 확률, (c) 오늘과 내일 모두 비가 올 확률, (d) 오늘 또는 내일 비가 올 확률, 그는 심사숙고 끝에 30%, 40%, 20%, 60%를 답으로 제시할 수도 있다. 불행히도, 이러한 답변(또는 이러한 주관적 확률)은 확률의 공리와 일치하지 않는다. (왜 일치하지 않을까?) 물론 우리는 응답자에게 이 점을 지적한 후 그가 답변을 바꿀 것이라고 기대할 것이다. (우리가 받아들일 수 있는 한 가지 가능성은 30%, 40%, 10%, 60%이다.)

Summary

$S$ 를 실험의 모든 가능한 결과들의 집합이라고 하자. $S$ 는 실험의 **표본 공간(sample space)**이라고 불린다. **사건(event)**은 $S$ 의 부분집합이다. 만약 $A_{i}, i=1, \ldots, n$ 가 사건들이라면, 이 사건들의 **합집합(union)**이라고 불리는 $\bigcup^{n} A_{i}$ 는 $A_{i}, i=1, \ldots, n$ 중 적어도 하나의 사건에 속하는 모든 결과들로 구성된다. 유사하게, 때때로 $A_{1} \cdots A_{n}$ 으로 쓰이는 $\bigcap_{i=1}^{n} A_{i}$ 는 사건 $A_{i}$ 들의 **교집합(intersection)**이라고 불리며, $A_{i}, i=1, \ldots, n$ 의 모든 사건에 속하는 모든 결과들로 구성된다.

어떤 사건 $A$ 에 대해서도, 우리는 $A^{c}$ 를 표본 공간에서 $A$ 에 속하지 않는 모든 결과들로 구성된다고 정의한다. 우리는 $A^{c}$ 를 사건 $A$ 의 **여집합(complement)**이라고 부른다. 결과가 없는 사건 $S^{c}$ 는 $\varnothing$ 으로 지정되며 **공집합(null set)**이라고 불린다. 만약 $A B=\varnothing$ 이면, 우리는 $A$ 와 $B$ 가 **상호 배타적(mutually exclusive)**이라고 말한다.

표본 공간 $S$ 의 각 사건 $A$ 에 대해, 우리는 $A$ 의 **확률(probability)**이라고 불리는 숫자 $P(A)$ 가 정의되며 다음과 같다고 가정한다: (i) $0 \leq P(A) \leq 1$ (ii) $P(S)=1$ (iii) 상호 배타적인 사건 $A_{i}, i \geq 1$ 에 대해,

P\left(\bigcup_{i=1}^{\infty} A_{i}\right)=\sum_{i=1}^{\infty} P\left(A_{i}\right)

$P(A)$ 는 실험의 결과가 $A$ 에 속할 확률을 나타낸다.

다음이 성립함을 보일 수 있다.

P\left(A^{c}\right)=1-P(A)

유용한 결과는 다음과 같다.

P(A \cup B)=P(A)+P(B)-P(A B)

이는 다음과 같이 일반화될 수 있다.

\begin{aligned} P\left(\bigcup_{i=1}^{n} A_{i}\right)= & \sum_{i=1}^{n} P\left(A_{i}\right)-\sum_{i<j} \sum_{i} P\left(A_{i} A_{j}\right) \\ & +\sum \sum \sum P\left(A_{i} A_{j} A_{k}\right) \\ & +\cdots+(-1)^{n+1} P\left(A_{1} \cdots A_{n}\right) \end{aligned}

이 결과는 **포함-배제 원리(inclusion-exclusion identity)**로 알려져 있다.

만약 $S$ 가 유한하고 각 한 점 집합이 동일한 확률을 가진다고 가정하면,

P(A)=\frac{|A|}{|S|}

여기서 $|E|$ 는 사건 $E$ 에 있는 결과의 수를 나타낸다. $P(A)$ 는 장기적인 상대 빈도(long-run relative frequency) 또는 **믿음의 정도(degree of belief)**의 척도로 해석될 수 있다.

Problems

상자에는 빨간색 1개, 녹색 1개, 파란색 1개의 구슬 3개가 들어 있다. 상자에서 구슬 1개를 꺼낸 다음 다시 상자에 넣고 두 번째 구슬을 꺼내는 실험을 고려해 보자. **표본 공간(sample space)**을 설명하시오. 첫 번째 구슬을 다시 넣지 않고 두 번째 구슬을 꺼낼 때도 반복하시오.
한 실험에서 주사위를 계속 굴리다가 6이 나오면 실험을 중단한다. 이 실험의 표본 공간은 무엇인가? $E_{n}$ 을 실험을 완료하는 데 $n$ 번의 굴림이 필요한 사건이라고 하자. 표본 공간의 어떤 점들이 $E_{n}$ 에 포함되는가? $\left(\bigcup_{1}^{\infty} E_{n}\right)^{c}$ 는 무엇인가?
두 개의 주사위를 던진다. $E$ 를 주사위의 합이 홀수인 사건, $F$ 를 적어도 하나의 주사위가 1이 나오는 사건, $G$ 를 합이 5인 사건이라고 하자. 사건 $E F, E \cup F, F G, E F^{c}$ , 그리고 $E F G$ 를 설명하시오.
$A, B, C$ 가 번갈아 가며 동전을 던진다. 먼저 앞면이 나오는 사람이 이긴다. 이 실험의 표본 공간은 다음과 같이 정의될 수 있다.
$S=\left\{\begin{array}{l} 1,01,001,0001, \ldots \\ 0000 \ldots \end{array}\right.$
(a) 표본 공간을 해석하시오. (b) 다음 사건들을 $S$ 의 관점에서 정의하시오: (i) $A$ 가 이김 $=A$ . (ii) $B$ 가 이김 $=B$ . (iii) $(A \cup B)^{c}$ .

$A$ 가 먼저 던지고, 그 다음 $B$ , 그 다음 $C$ , 그 다음 $A$ 순으로 계속된다고 가정한다.
시스템은 5개의 구성 요소로 이루어져 있으며, 각 구성 요소는 작동 중이거나 고장 난 상태이다. 각 구성 요소의 상태를 관찰하는 실험을 고려하고, 실험의 결과는 벡터 $\left(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right)$ 로 주어진다고 하자. 여기서 $x_{i}$ 는 구성 요소 $i$ 가 작동 중이면 1이고, 고장 났으면 0이다. (a) 이 실험의 표본 공간에는 몇 개의 결과가 있는가? (b) 구성 요소 1과 2가 모두 작동 중이거나, 구성 요소 3과 4가 모두 작동 중이거나, 구성 요소 1, 3, 5가 모두 작동 중이면 시스템이 작동한다고 가정하자. $W$ 를 시스템이 작동하는 사건이라고 하자. $W$ 에 있는 모든 결과를 명시하시오. (c) $A$ 를 구성 요소 4와 5가 모두 고장 난 사건이라고 하자. 사건 $A$ 에는 몇 개의 결과가 포함되는가? (d) 사건 $A W$ 에 있는 모든 결과를 작성하시오.
병원 관리자는 총상 환자를 보험 유무(보험이 있으면 1, 없으면 0)와 상태(양호(g), 보통(f), 심각(s))에 따라 코딩한다. 이러한 환자를 코딩하는 실험을 고려해 보자. (a) 이 실험의 표본 공간을 제시하시오. (b) $A$ 를 환자가 심각한 상태인 사건이라고 하자. $A$ 에 있는 결과를 명시하시오. (c) $B$ 를 환자가 무보험인 사건이라고 하자. $B$ 에 있는 결과를 명시하시오. (d) 사건 $B^{c} \cup A$ 에 있는 모든 결과를 제시하시오.
성인 축구팀 15명의 직업 유형(블루칼라 또는 화이트칼라)과 정치적 소속(공화당, 민주당 또는 무소속)을 결정하는 실험을 고려해 보자. 다음의 경우 결과는 몇 개인가? (a) 표본 공간에 있는 경우 (b) 팀원 중 적어도 한 명이 블루칼라 노동자인 사건에 있는 경우 (c) 팀원 중 아무도 자신을 무소속이라고 생각하지 않는 사건에 있는 경우
$A$ 와 $B$ 가 상호 배타적인 사건이고 $P(A)=.3$ , $P(B)=.5$ 라고 가정하자. 다음의 확률은 얼마인가? (a) $A$ 또는 $B$ 가 발생하는 경우 (b) $A$ 는 발생하지만 $B$ 는 발생하지 않는 경우 (c) $A$ 와 $B$ 가 모두 발생하는 경우
어떤 소매점은 American Express 또는 VISA 신용카드를 받는다. 고객 중 24%는 American Express 카드를 소지하고, 61%는 VISA 카드를 소지하며, 11%는 두 카드 모두 소지한다. 이 소매점에서 받을 수 있는 신용카드를 소지한 고객은 몇 퍼센트인가?
특정 학교 학생의 60%는 반지나 목걸이를 착용하지 않는다. 20%는 반지를 착용하고 30%는 목걸이를 착용한다. 학생 중 한 명을 무작위로 선택했을 때, 이 학생이 다음을 착용하고 있을 확률은 얼마인가? (a) 반지 또는 목걸이 (b) 반지와 목걸이
미국 남성의 28%는 담배를 피우고, 7%는 시가를 피우며, 5%는 시가와 담배를 모두 피운다. (a) 시가도 담배도 피우지 않는 남성은 몇 퍼센트인가? (b) 시가는 피우지만 담배는 피우지 않는 남성은 몇 퍼센트인가?
한 초등학교에서 3개의 언어 수업을 제공한다: 스페인어, 프랑스어, 독일어. 이 수업은 학교의 100명 학생 중 누구에게나 열려 있다. 스페인어 수업에는 28명, 프랑스어 수업에는 26명, 독일어 수업에는 16명의 학생이 있다. 스페인어와 프랑스어 모두 수강하는 학생은 12명, 스페인어와 독일어 모두 수강하는 학생은 4명, 프랑스어와 독일어 모두 수강하는 학생은 6명이다. 또한, 3가지 수업을 모두 수강하는 학생은 2명이다. (a) 학생 한 명을 무작위로 선택했을 때, 그 학생이 어떤 언어 수업도 듣지 않을 확률은 얼마인가? (b) 학생 한 명을 무작위로 선택했을 때, 그 학생이 정확히 한 가지 언어 수업만 듣고 있을 확률은 얼마인가? (c) 학생 두 명을 무작위로 선택했을 때, 적어도 한 명이 언어 수업을 듣고 있을 확률은 얼마인가?
인구 100,000명의 특정 도시에 3개의 신문(I, II, III)이 있다. 이 신문을 읽는 시민의 비율은 다음과 같다:

I: 10 percent I and II: 8 percent I and II and III: 1 percent

II: 30 percent I and III: 2 percent <br> III: 5 percent II and III: 4 percent

(이 목록은 예를 들어 8000명이 신문 I과 II를 읽는다는 것을 알려준다.) (a) 신문 한 가지만 읽는 사람들의 수를 구하시오. (b) 적어도 두 개의 신문을 읽는 사람은 몇 명인가? (c) I과 III이 조간신문이고 II가 석간신문이라면, 적어도 하나의 조간신문과 하나의 석간신문을 읽는 사람은 몇 명인가? (d) 신문을 전혀 읽지 않는 사람은 몇 명인가? (e) 조간신문 한 개와 석간신문 한 개만 읽는 사람은 몇 명인가? 14. 특정 잡지의 구독자 1000명으로 구성된 그룹에 대한 연구에서 다음과 같은 데이터가 주어졌다: 직업, 혼인 여부, 교육 수준과 관련하여, 전문가 312명, 기혼자 470명, 대학 졸업자 525명, 전문직 대학 졸업자 42명, 기혼 대학 졸업자 147명, 기혼 전문직 86명, 기혼 전문직 대학 졸업자 25명이 있었다. 이 연구에서 보고된 숫자들이 틀렸음을 보이시오.

힌트: $M, W, G$ 를 각각 전문가, 기혼자, 대학 졸업자 집합이라고 하자. 1000명 중 한 명이 무작위로 선택된다고 가정하고, 주어진 숫자들이 정확하다면 $P(M \cup W \cup G)>1$ 임을 보이기 위해 명제 4.4를 사용하시오. 15. 모든 $\binom{52}{5}$ 포커 패가 동일하게 나올 확률이라고 가정할 때, 다음 패를 받을 확률은 얼마인가? (a) 플러시? (모든 5장의 카드가 같은 무늬일 때 플러시라고 한다.) (b) 원 페어? (카드의 액면가가 $a, a, b, c, d$ 이고 $a, b, c, d$ 가 모두 다를 때 발생한다.) (c) 투 페어? (카드의 액면가가 $a, a, b, b, c$ 이고 $a, b, c$ 가 모두 다를 때 발생한다.) (d) 쓰리 오브 어 카인드? (카드의 액면가가 $a, a, a, b, c$ 이고 $a, b, c$ 가 모두 다를 때 발생한다.) (e) 포 오브 어 카인드? (카드의 액면가가 $a, a, a, a, b$ 일 때 발생한다.) 16. 포커 주사위는 5개의 주사위를 동시에 굴려서 플레이한다. 다음을 보이시오. (a) $P\{$ 두 개도 같지 않음 $\}=.0926$ ; (b) $P\{$ 원 페어 $\}=.4630$ ; (c) $P\{$ 투 페어 $\}=.2315$ ; (d) $P\{$ 쓰리 오브 어 카인드 $\}=.1543$ ; (e) $P\{$ 풀 하우스 $\}=.0386$ ; (f) $P\{$ 포 오브 어 카인드 $\}=.0193$ ; (g) $P\{$ 파이브 오브 어 카인드 $\}=.0008$ . 17. 8개의 룩(성)이 체스판에 무작위로 놓일 때, 어떤 룩도 다른 룩을 잡을 수 없을 확률을 계산하시오. 즉, 어떤 행이나 열에도 룩이 두 개 이상 포함되지 않을 확률을 계산하시오. 18. 일반적인 플레잉 카드 덱에서 두 장의 카드를 무작위로 선택한다. 이들이 블랙잭을 형성할 확률은 얼마인가? 즉, 한 장의 카드가 에이스이고 다른 한 장이 텐, 잭, 퀸 또는 킹일 확률은 얼마인가? 19. 두 개의 대칭 주사위의 두 면은 빨간색, 두 면은 검은색, 한 면은 노란색, 다른 한 면은 흰색으로 칠해져 있다. 이 한 쌍의 주사위를 굴릴 때, 두 주사위 모두 같은 색 면이 위로 향할 확률은 얼마인가? 20. 딜러와 블랙잭을 플레이한다고 가정하자. 새로 섞은 덱에서 당신과 딜러 모두 블랙잭을 받지 않을 확률은 얼마인가? 21. 작은 지역 사회 조직은 20가구로 구성되어 있으며, 이 중 4가구는 자녀가 1명, 8가구는 자녀가 2명, 5가구는 자녀가 3명, 2가구는 자녀가 4명, 1가구는 자녀가 5명이다. (a) 이 가구 중 하나를 무작위로 선택할 때, 자녀가 $i$ 명일 확률은 얼마인가? ( $i=1,2,3,4,5$ ) (b) 자녀 중 한 명을 무작위로 선택할 때, 그 자녀가 자녀가 $i$ 명인 가구 출신일 확률은 얼마인가? ( $i=1,2,3,4,5$ ) 22. $n$ 장의 카드 덱을 섞는 다음 기술을 고려하시오: 카드의 어떤 초기 순서에 대해서도, 한 번에 한 장씩 덱을 통과하며 각 카드에서 공정한 동전을 던진다. 동전이 앞면이 나오면 카드를 그 자리에 두고, 뒷면이 나오면 그 카드를 덱의 끝으로 옮긴다. 동전이 $n$ 번 던져진 후, 한 라운드가 완료되었다고 말한다. 예를 들어, $n=4$ 이고 초기 순서가 $1,2,3,4$ 일 때, 연속적인 동전 던지기 결과가 $h, t, t, h$ 라면, 라운드 끝의 순서는 $1,4,2,3$ 이다. $n$ 번의 동전 던지기 시퀀스의 모든 가능한 결과가 동일하게 나올 확률이라고 가정할 때, 한 라운드 후의 순서가 초기 순서와 같을 확률은 얼마인가? 23. 공정한 주사위 한 쌍을 굴린다. 두 번째 주사위가 첫 번째 주사위보다 높은 값으로 나올 확률은 얼마인가? 24. 두 개의 주사위를 굴릴 때, 위로 향한 면의 합이 $i$ 와 같을 확률은 얼마인가? $i=2,3, \ldots, 11,12$ 에 대해 구하시오. 25. 합이 5 또는 7이 나올 때까지 한 쌍의 주사위를 굴린다. 5가 먼저 나올 확률을 구하시오. 힌트: $E_{n}$ 을 $n$ 번째 굴림에서 5가 나오고 처음 $n-1$ 번의 굴림에서는 5나 7이 나오지 않는 사건이라고 하자. $P\left(E_{n}\right)$ 을 계산하고 $\sum_{n=1}^{\infty} P\left(E_{n}\right)$ 이 원하는 확률임을 주장하시오. 26. 크랩스 게임은 다음과 같이 진행된다: 플레이어가 두 개의 주사위를 굴린다. 주사위의 합이 2, 3 또는 12이면 플레이어는 지고, 합이 7 또는 11이면 플레이어는 이긴다. 결과가 다른 것이면, 플레이어는 초기 결과 또는 7이 나올 때까지 주사위를 계속 굴린다. 7이 먼저 나오면 플레이어는 지고, 7이 나오기 전에 초기 결과가 다시 나오면 플레이어는 이긴다. 크랩스에서 플레이어가 이길 확률을 계산하시오. 힌트: $E_{i}$ 를 초기 결과가 $i$ 이고 플레이어가 이기는 사건이라고 하자. 원하는 확률은 $\sum_{i=2}^{12} P\left(E_{i}\right)$ 이다. $P\left(E_{i}\right)$ 를 계산하기 위해, $E_{i, n}$ 을 초기 합이 $i$ 이고 플레이어가 $n$ 번째 굴림에서 이기는 사건이라고 정의하자. $P\left(E_{i}\right)=\sum_{n=1}^{\infty} P\left(E_{i, n}\right)$ 임을 주장하시오. 27. 항아리에 빨간 공 3개와 검은 공 7개가 들어 있다. 플레이어 $A$ 와 $B$ 는 빨간 공이 선택될 때까지 항아리에서 공을 연속적으로 뽑는다. $A$ 가 빨간 공을 뽑을 확률을 구하시오. ( $A$ 가 첫 번째 공을 뽑고, 그 다음 $B$ , 이런 식으로 진행된다. 뽑은 공은 다시 넣지 않는다.) 28. 항아리에 빨간 공 5개, 파란 공 6개, 초록 공 8개가 들어 있다. 3개의 공을 무작위로 선택할 때, 각 공이 (a) 같은 색일 확률은 얼마인가? (b) 다른 색일 확률은 얼마인가? 공을 선택할 때마다 색깔을 확인하고 다음 선택 전에 항아리에 다시 넣는다고 가정하고 반복하시오. 이것을 복원 추출이라고 한다. 29. 항아리에 $n$ 개의 흰 공과 $m$ 개의 검은 공이 들어 있으며, $n$ 과 $m$ 은 양수이다. (a) 두 개의 공을 무작위로 뽑을 때, 같은 색일 확률은 얼마인가? (b) 공 하나를 무작위로 뽑고 두 번째 공을 뽑기 전에 다시 넣을 때, 뽑은 공들이 같은 색일 확률은 얼마인가? (c) (b)의 확률이 (a)의 확률보다 항상 크다는 것을 보이시오. 30. 두 학교의 체스 클럽은 각각 8명과 9명의 선수로 구성되어 있다. 각 클럽에서 4명의 회원이 무작위로 선택되어 두 학교 간의 대회에 참가한다. 한 팀에서 선택된 선수들은 다른 팀의 선수들과 무작위로 짝을 이루고, 각 짝은 체스 게임을 한다. 레베카와 그녀의 여동생 엘리스가 다른 학교의 체스 클럽에 있다고 가정하자. 다음 확률은 얼마인가? (a) 레베카와 엘리스가 짝을 이룰 확률? (b) 레베카와 엘리스가 학교를 대표하도록 선택되지만 서로 경기를 하지 않을 확률? (c) 레베카 또는 엘리스가 학교를 대표하도록 선택될 확률? 31. 3인 농구팀은 가드, 포워드, 센터로 구성된다. (a) 세 개의 다른 팀에서 각각 한 명씩 무작위로 선택할 때, 완전한 팀을 구성할 확률은 얼마인가? (b) 선택된 3명의 선수 모두 같은 포지션을 플레이할 확률은 얼마인가? 32. $b$ 명의 소년과 $g$ 명의 소녀로 구성된 그룹이 무작위 순서로 줄을 선다. 즉, $(b+g)!$ 개의 모든 순열이 동일하게 나올 확률이라고 가정한다. $i$ 번째 위치( $1 \leq i \leq b+g$ )에 있는 사람이 소녀일 확률은 얼마인가? 33. 숲에 20마리의 엘크가 있는데, 그 중 5마리가 잡혀서 태그가 부착된 후 방사된다. 얼마 후, 20마리의 엘크 중 4마리가 잡힌다. 이 4마리 중 2마리가 태그가 부착된 엘크일 확률은 얼마인가? 어떤 가정을 하고 있는가? 34. 야보로 백작 2세는 13장의 브리지 패에 텐 이상의 카드가 적어도 한 장 포함될 확률이 1000대 1이라고 내기했다고 전해진다. (텐 이상이란 카드가 텐, 잭, 퀸, 킹 또는 에이스 중 하나임을 의미한다.) 오늘날 우리는 9보다 높은 카드가 없는 패를 야보로라고 부른다. 무작위로 선택된 브리지 패가 야보로일 확률은 얼마인가? 35. 빨간 공 12개, 파란 공 16개, 초록 공 18개가 들어 있는 항아리에서 7개의 공을 무작위로 뽑는다. 다음 확률을 구하시오. (a) 빨간 공 3개, 파란 공 2개, 초록 공 2개가 뽑힐 확률; (b) 적어도 2개의 빨간 공이 뽑힐 확률; (c) 뽑힌 모든 공이 같은 색일 확률; (d) 정확히 빨간 공 3개 또는 정확히 파란 공 3개가 뽑힐 확률. 36. 52장의 플레잉 카드 덱에서 두 장의 카드를 무작위로 선택한다. 다음 확률은 얼마인가? (a) 둘 다 에이스일 확률? (b) 같은 값을 가질 확률? 37. 강사가 학생들에게 10개의 문제 세트를 주고, 기말고사는 그 중 5개를 무작위로 선택하여 출제될 것이라고 알려준다. 한 학생이 7개의 문제를 푸는 방법을 알아냈다면, 그 학생이 다음을 정확하게 답할 확률은 얼마인가? (a) 5개의 문제 모두? (b) 적어도 4개의 문제? 38. 서랍에 $n$ 개의 양말이 있는데, 그 중 3개는 빨간색이다. 양말 2개를 무작위로 선택했을 때, 둘 다 빨간색일 확률이 $\frac{1}{2}$ 이라면 $n$ 의 값은 얼마인가? 39. 특정 마을에 5개의 호텔이 있다. 하루에 3명이 호텔에 체크인할 때, 각자 다른 호텔에 체크인할 확률은 얼마인가? 어떤 가정을 하고 있는가? 40. 마을에 텔레비전을 수리하는 사람이 4명 있다. 4대의 텔레비전이 고장 났을 때, 정확히 $i$ 명의 수리공이 불려갈 확률은 얼마인가? $i=1,2,3,4$ 에 대해 문제를 푸시오. 어떤 가정을 하고 있는가? 41. 주사위를 4번 굴릴 때, 6이 적어도 한 번 나올 확률은 얼마인가? 42. 두 개의 주사위를 연속으로 $n$ 번 던진다. 더블 6이 적어도 한 번 나올 확률을 계산하시오. 이 확률이 적어도 $\frac{1}{2}$ 이 되려면 $n$ 은 얼마나 커야 하는가? 43. (a) $A$ 와 $B$ 를 포함한 $N$ 명의 사람들이 무작위로 일렬로 배열될 때, $A$ 와 $B$ 가 서로 옆에 있을 확률은 얼마인가? (b) 사람들이 무작위로 원형으로 배열될 경우 확률은 얼마인가? 44. $A, B, C, D, E$ 로 지정된 5명의 사람들이 일렬로 배열된다. 가능한 모든 순서가 동일하게 나올 확률이라고 가정할 때, 다음 확률은 얼마인가? (a) $A$ 와 $B$ 사이에 정확히 한 사람이 있을 확률? (b) $A$ 와 $B$ 사이에 정확히 두 사람이 있을 확률? (c) $A$ 와 $B$ 사이에 세 사람이 있을 확률? 45. 한 여성이 $n$ 개의 열쇠를 가지고 있는데, 그 중 하나가 문을 열 수 있다. (a) 그녀가 열쇠를 무작위로 시도하고 작동하지 않는 열쇠는 버린다면, $k$ 번째 시도에서 문을 열 확률은 얼마인가? (b) 이전에 시도한 열쇠를 버리지 않는다면? 46. 방에 몇 명의 사람이 있어야 그들 중 적어도 두 명이 같은 달에 생일을 축하할 확률이 적어도 $\frac{1}{2}$ 이 되는가? 가능한 모든 월별 결과가 동일하게 나올 확률이라고 가정하시오. 47. 방에 12명의 낯선 사람이 있다면, 그들 중 두 명도 같은 달에 생일을 축하하지 않을 확률은 얼마인가? 48. 20명의 사람이 주어졌을 때, 1년 중 12개월 중에서 정확히 2개의 생일을 포함하는 달이 4개이고 정확히 3개의 생일을 포함하는 달이 4개일 확률은 얼마인가? 49. 6명의 남성과 6명의 여성으로 구성된 그룹이 각각 6명씩 2개의 그룹으로 무작위로 나뉜다. 두 그룹 모두 같은 수의 남성을 가질 확률은 얼마인가? 50. 브리지 패에서, 당신이 스페이드 5장을 가지고 있고 당신의 파트너가 나머지 8장을 가질 확률을 구하시오. 51. $n$ 개의 공이 $N$ 개의 칸에 무작위로 분배된다고 가정하자. 첫 번째 칸에 $m$ 개의 공이 들어갈 확률을 구하시오. 모든 $N^{n}$ 개의 배열이 동일하게 나올 확률이라고 가정하시오. 52. 옷장에는 10켤레의 신발이 들어 있다. 8개의 신발을 무작위로 선택할 때, 다음 확률은 얼마인가? (a) 완전한 짝이 없을 확률? (b) 정확히 1개의 완전한 짝이 있을 확률? 53. 4쌍의 부부가 일렬로 배열될 때, 어떤 남편도 아내 옆에 앉지 않을 확률을 구하시오. 54. 브리지 패가 적어도 한 무늬에서 보이드일 확률을 계산하시오. 답이 다음이 아님에 유의하시오.

\frac{\binom{4}{1}\binom{39}{13}}{\binom{52}{13}}

(왜 아닌가?) 힌트: 명제 4.4를 사용하시오. 55. 13장의 카드 패가 다음을 포함할 확률을 계산하시오. (a) 적어도 한 무늬의 에이스와 킹; (b) 13개의 액면가 중 적어도 1개의 모든 4장. 56. 두 플레이어가 다음 게임을 한다: 플레이어 $A$ 는 그림 2.6에 묘사된 세 개의 스피너 중 하나를 선택하고, 그 다음 플레이어 $B$ 는 나머지 두 스피너 중 하나를 선택한다. 두 플레이어는 각자의 스피너를 돌리고, 더 높은 숫자에 멈춘 사람이 승자로 선언된다. 각 스피너가 3개의 영역 중 어느 곳에나 동일하게 멈출 확률이라고 가정할 때, 당신은 플레이어 $A$ 가 되고 싶은가 아니면 플레이어 $B$ 가 되고 싶은가? 당신의 답변을 설명하시오!

그림 2.6 스피너.

Theoretical Exercises

다음 관계를 증명하시오:

$E F \subset E \subset E \cup F$ .
만약 $E \subset F$ 이면, $F^{c} \subset E^{c}$ 이다.
$F=F E \cup F E^{c}$ 이고 $E \cup F=E \cup E^{c} F$ 이다.
$\left(\bigcup_{1}^{\infty} E_{i}\right) F=\bigcup_{1}^{\infty} E_{i} F$ 이고 $\left(\bigcap_{1}^{\infty} E_{i}\right) \cup F=\bigcap_{1}^{\infty}\left(E_{i} \cup F\right)$ 이다.
임의의 사건 시퀀스 $E_{1}, E_{2}, \ldots$ 에 대해, 서로소 사건(즉, $i \neq j$ 일 때 $F_{i} F_{j}=\varnothing$ 인 사건)의 새로운 시퀀스 $F_{1}, F_{2}, \ldots$ 를 정의하여 모든 $n \geq 1$ 에 대해 다음이 성립하도록 하시오.

\bigcup_{1}^{n} F_{i}=\bigcup_{1}^{n} E_{i}

$E, F, G$ 가 세 가지 사건이라고 하자. $E, F, G$ 중에서 다음이 발생하는 사건에 대한 표현을 찾으시오. (a) $E$ 만 발생한다; (b) $E$ 와 $G$ 는 발생하지만 $F$ 는 발생하지 않는다; (c) 적어도 하나의 사건이 발생한다; (d) 적어도 두 개의 사건이 발생한다; (e) 세 가지 사건 모두 발생한다; (f) 어떤 사건도 발생하지 않는다; (g) 많아야 하나의 사건이 발생한다; (h) 많아야 두 개의 사건이 발생한다; (i) 정확히 두 개의 사건이 발생한다; (j) 많아야 세 개의 사건이 발생한다.
벤 다이어그램을 사용하여 (a) $(E \cup F)\left(E \cup F^{c}\right)$ 표현을 단순화하시오; (b) 사건 $E$ 와 $F$ 에 대한 드 모르간의 법칙을 증명하시오. [즉, $(E \cup F)^{c}=E^{c} F^{c}$ 및 $(E F)^{c}=E^{c} \cup F^{c}$ 를 증명하시오.]
$S$ 가 주어진 집합이라고 하자. 만약 어떤 $k>0$ 에 대해 $S_{1}, S_{2}, \ldots, S_{k}$ 가 $S$ 의 서로 배타적인 공집합이 아닌 부분집합이고 $\bigcup_{i=1}^{k} S_{i}=S$ 이면, 집합 $\left\{S_{1}, S_{2}, \ldots, S_{k}\right\}$ 를 $S$ 의 **분할(partition)**이라고 부른다. $T_{n}$ 을 $\{1,2, \ldots, n\}$ 의 서로 다른 분할의 수라고 하자. 따라서 $T_{1}=1$ (유일한 분할은 $S_{1}=\{1\}$ )이고 $T_{2}=2$ (두 가지 분할은 $\{\{1,2\}\},\{\{1\},\{2\}\}$ )이다. (a) 모든 분할을 계산하여 $T_{3}=5, T_{4}=15$ 임을 보이시오. (b) 다음을 보이시오.

T_{n+1}=1+\sum_{k=1}^{n}\binom{n}{k} T_{k}

그리고 이 방정식을 사용하여 $T_{10}$을 계산하시오.
힌트: $n+1$개의 항목을 분할하는 한 가지 방법은 항목 중 하나를 특별하다고 부르는 것이다. 그런 다음 $k, k=0,1, \ldots, n$를 먼저 선택하고, 비특별 항목 중 $n-k$ 크기의 부분집합을 선택한 다음, 나머지 $k$개의 비특별 항목의 $T_{k}$ 분할 중 하나를 선택하여 다른 분할을 얻는다. 특별 항목을 $n-k$ 크기의 부분집합에 추가함으로써 모든 $n+1$개 항목의 분할을 얻는다.

9. 어떤 실험이 $n$ 번 수행된다고 가정하자. 표본 공간의 임의의 사건 $E$ 에 대해 $n(E)$ 를 사건 $E$ 가 발생하는 횟수라고 하고 $f(E)=n(E) / n$ 으로 정의하자. $f(\cdot)$ 가 공리 1, 2, 3을 만족함을 보이시오. 10. $P(E \cup F \cup G)=P(E)+P(F)+P(G)- P\left(E^{c} F G\right)-P\left(E F^{c} G\right)-P\left(E F G^{c}\right)-2 P(E F G)$ 임을 증명하시오. 11. 만약 $P(E)=.9$ 이고 $P(F)=.8$ 이면, $P(E F) \geq .7$ 임을 보이시오. 일반적으로 본페로니 부등식(Bonferroni's inequality), 즉 다음을 증명하시오.

P(E F) \geq P(E)+P(F)-1

사건 $E$ 또는 $F$ 중 정확히 하나가 발생할 확률이 $P(E)+P(F)-2 P(E F)$ 와 같음을 보이시오.
$P\left(E F^{c}\right)=P(E)-P(E F)$ 임을 증명하시오.
수학적 귀납법으로 명제 4.4를 증명하시오.
항아리에 $M$ 개의 흰 공과 $N$ 개의 검은 공이 들어 있다. 크기 $r$ 의 무작위 표본을 선택할 때, 정확히 $k$ 개의 흰 공이 포함될 확률은 얼마인가?
귀납법을 사용하여 본페로니 부등식을 $n$ 개의 사건으로 일반화하시오. 즉, 다음을 보이시오.

P\left(E_{1} E_{2} \cdots E_{n}\right) \geq P\left(E_{1}\right)+\cdots+P\left(E_{n}\right)-(n-1)

매칭 문제(예제 5m)를 고려하고, $N$ 명의 남자가 자신의 모자를 선택하지 않는 방법의 수를 $A_{N}$ 이라고 정의하자. 다음을 주장하시오.

A_{N}=(N-1)\left(A_{N-1}+A_{N-2}\right)

이 공식은 경계 조건 $A_{1}=0, A_{2}=1$과 함께 $A_{N}$을 풀 수 있으며, 일치하지 않을 원하는 확률은 $A_{N} / N!$이 될 것이다.
힌트: 첫 번째 남자가 자신의 모자가 아닌 모자를 선택한 후, $N-1$명의 남자가 이들 중 한 명의 모자를 포함하지 않는 $N-1$개의 모자 중에서 선택해야 한다. 따라서 한 명의 추가 남자와 한 개의 추가 모자가 있다. 추가 남자가 추가 모자를 선택하는 경우 또는 추가 남자가 추가 모자를 선택하지 않는 경우 모두 일치가 발생하지 않을 수 있음을 주장하시오.

18. 동전을 $n$ 번 던져서 연속적인 앞면이 나타나지 않는 방법의 수를 $f_{n}$ 이라고 하자. 다음을 주장하시오.

f_{n}=f_{n-1}+f_{n-2} \quad n \geq 2, \text { 여기서 } f_{0} \equiv 1, f_{1} \equiv 2

힌트: 앞면으로 시작하는 결과는 몇 개이고, 뒷면으로 시작하는 결과는 몇 개인가? $n$번 동전을 던질 때 연속적인 앞면이 나타나지 않을 확률을 $P_{n}$이라고 할 때, $n$번 던진 모든 가능한 결과가 동일하게 발생할 가능성이 있다고 가정할 때 $P_{n}$을 ($f_{n}$으로 표현하여) 찾으시오. $P_{10}$을 계산하시오.

19. 항아리에 $n$ 개의 빨간 공과 $m$ 개의 파란 공이 들어 있다. 총 $r, r \leq n$ 개의 빨간 공이 뽑힐 때까지 한 번에 하나씩 공을 뽑는다. 총 $k$ 개의 공이 뽑힐 확률을 구하시오. 힌트: 첫 $k-1$ 번의 뽑기에서 $r-1$ 개의 빨간 공이 있고 $k$ 번째 뽑기가 빨간 공이면 총 $k$ 개의 공이 뽑힐 것이다. 20. 표본 공간이 셀 수 없이 많은 수의 점으로 구성된 실험을 고려하시오. 모든 점이 동일하게 발생할 가능성이 있을 수 없음을 보이시오. 모든 점이 발생할 양의 확률을 가질 수 있는가? *21. 예제 5o를 고려하시오. 이 예제는 $n$ 번의 승리와 $m$ 번의 패배가 무작위로 순열될 때 얻어지는 승리 **런(run)**의 수에 관한 것이다. 이제 총 런의 수, 즉 승리 런과 패배 런의 합을 고려하고 다음을 보이시오.

\begin{aligned} & P\{2 k \text { runs }\}=2 \frac{\binom{m-1}{k-1}\binom{n-1}{k-1}}{\binom{m+n}{n}} \\ & P\{2 k+1 \text { runs }\} \\ & =\frac{\binom{m-1}{k-1}\binom{n-1}{k}+\binom{m-1}{k}\binom{n-1}{k-1}}{\binom{m+n}{n}} \end{aligned}

Self-Test Problems and Exercises

한 식당에서 앙트레, 전분, 디저트로 구성된 3코스 식사를 제공한다. 가능한 선택지는 다음 표와 같다:

코스	선택지
앙트레	치킨 또는 로스트 비프
전분	파스타 또는 밥 또는 감자
디저트	아이스크림 또는 젤로 또는 애플 파이 또는 복숭아

한 사람은 각 카테고리에서 하나의 코스를 선택해야 한다. (a) 표본 공간에는 몇 개의 결과가 있는가? (b) 아이스크림이 선택되는 사건을 $A$ 라고 하자. $A$ 에는 몇 개의 결과가 있는가? (c) 치킨이 선택되는 사건을 $B$ 라고 하자. $B$ 에는 몇 개의 결과가 있는가? (d) 사건 $A B$ 의 모든 결과를 나열하라. (e) 밥이 선택되는 사건을 $C$ 라고 하자. $C$ 에는 몇 개의 결과가 있는가? (f) 사건 $A B C$ 의 모든 결과를 나열하라. 2. 특정 상점의 양복 코너를 방문하는 고객이 양복을 구매할 확률은 .22, 셔츠를 구매할 확률은 .30, 넥타이를 구매할 확률은 .28이다. 고객이 양복과 셔츠를 모두 구매할 확률은 .11, 양복과 넥타이를 모두 구매할 확률은 .14, 셔츠와 넥타이를 모두 구매할 확률은 .10이다. 고객이 세 가지 품목을 모두 구매할 확률은 .06이다. 고객이 다음을 구매할 확률은 얼마인가? (a) 이 품목들 중 아무것도 구매하지 않을 확률 (b) 이 품목들 중 정확히 1개만 구매할 확률 3. 카드 한 벌이 나누어진다. 14번째로 나누어진 카드가 에이스일 확률은 얼마인가? 첫 번째 에이스가 14번째 카드에서 나올 확률은 얼마인가? 4. 로스앤젤레스 시내 온도가 $70^{\circ} \mathrm{F}$ 인 사건을 $A$ 라고 하고, 뉴욕 시내 온도가 $70^{\circ} \mathrm{F}$ 인 사건을 $B$ 라고 하자. 또한, 뉴욕과 로스앤젤레스 시내 온도 중 최댓값이 $70^{\circ} \mathrm{F}$ 인 사건을 $C$ 라고 하자. 만약 $P(A)=.3, P(B)=.4$ , 그리고 $P(C)=.2$ 라면, 두 시내 온도 중 최솟값이 $70^{\circ} \mathrm{F}$ 일 확률을 구하라. 5. 52장의 일반적인 카드 덱이 섞인다. 상위 4장의 카드가 다음을 가질 확률은 얼마인가? (a) 다른 덴오미네이션(denominations)? (b) 다른 슈트(suits)? 6. 항아리 $A$ 에는 빨간 공 3개와 검은 공 3개가 들어있고, 항아리 $B$ 에는 빨간 공 4개와 검은 공 6개가 들어있다. 각 항아리에서 공을 무작위로 하나씩 선택할 때, 두 공의 색깔이 같을 확률은 얼마인가? 7. 주 복권에서, 플레이어는 1부터 40까지의 숫자 중 8개를 선택해야 한다. 복권 위원회는 이 40개의 숫자 중 8개를 선택하는 실험을 수행한다. 복권 위원회의 선택이 $\binom{40}{8}$ 가지 조합 중 어느 하나일 확률이 동일하다고 가정할 때, 플레이어가 다음을 가질 확률은 얼마인가? (a) 복권 위원회가 선택한 8개의 숫자를 모두 맞출 확률 (b) 복권 위원회가 선택한 숫자 중 7개를 맞출 확률 (c) 복권 위원회가 선택한 숫자 중 적어도 6개를 맞출 확률 8. 1학년 학생 3명, 2학년 학생 4명, 3학년 학생 4명, 4학년 학생 3명으로 구성된 그룹에서 4명으로 구성된 위원회가 무작위로 선정된다. 위원회가 다음으로 구성될 확률을 구하라. (a) 각 학년에서 1명씩 (b) 2학년 2명과 3학년 2명 (c) 2학년 또는 3학년만 9. 유한 집합 $A$ 에 대해, $N(A)$ 를 $A$ 의 원소 개수라고 하자. (a) 다음을 보여라:

N(A \cup B)=N(A)+N(B)-N(A B)

(b) 더 일반적으로, 다음을 보여라:

\begin{aligned} N\left(\bigcup_{i=1}^{n} A_{i}\right)= & \sum_{i} N\left(A_{i}\right)-\sum_{i<j} \sum N\left(A_{i} A_{j}\right) \\ & +\cdots+(-1)^{n+1} N\left(A_{1} \cdots A_{n}\right) \end{aligned}

1번부터 6번까지 번호가 매겨진 6마리의 말이 경주를 하는 실험을 고려하고, 표본 공간은 말들이 결승선을 통과하는 6!가지 가능한 순서로 구성된다고 가정하자. 1번 말이 상위 3위 안에 드는 사건을 $A$ 라고 하고, 2번 말이 2위로 들어오는 사건을 $B$ 라고 하자. 사건 $A \cup B$ 에는 몇 개의 결과가 있는가?
잘 섞인 52장의 플레잉 카드 덱에서 5장의 카드가 뽑힌다. 이 패에 4가지 슈트 각각에서 적어도 한 장의 카드가 포함될 확률은 얼마인가?
농구팀은 프론트코트 선수 6명과 백코트 선수 4명으로 구성된다. 선수들이 무작위로 룸메이트로 나뉘어질 때, 백코트 선수와 프론트코트 선수로 구성된 룸메이트 쌍이 정확히 두 쌍이 될 확률은 얼마인가?
어떤 사람이 RESERVE에서 무작위로 한 글자를 선택하고, 그 다음 VERTICAL에서 무작위로 한 글자를 선택한다고 가정하자. 같은 글자가 선택될 확률은 얼마인가?
**부등식(Boole's inequality)**을 증명하라:

P\left(\bigcup_{i=1}^{\infty} A_{i}\right) \leq \sum_{i=1}^{\infty} P\left(A_{i}\right)

만약 모든 $i \geq 1$ 에 대해 $P\left(A_{i}\right)=1$ 이라면, $P\left(\bigcap_{i=1}^{\infty} A_{i}\right)=1$ 임을 보여라.
$T_{k}(n)$ 을 집합 $\{1, \ldots, n\}$ 을 $k$ 개의 비어 있지 않은 부분집합으로 분할하는 방법의 수라고 하자 (여기서 $1 \leq k \leq n$ ). (분할의 정의는 이론 연습 문제 8을 참조하라.) 다음을 논증하라:

T_{k}(n)=k T_{k}(n-1)+T_{k-1}(n-1)

힌트: $\{1\}$ 이 부분집합인 분할은 몇 개이며, 1이 다른 원소를 포함하는 부분집합의 원소인 분할은 몇 개인가? 17. 5개의 빨간 공, 6개의 흰 공, 7개의 파란 공이 들어있는 항아리에서 5개의 공을 비복원 추출로 무작위로 선택한다.

각 색깔의 공이 적어도 하나씩 선택될 확률을 구하라. 18. 빨간 공 4개, 파란 공 8개, 초록 공 5개가 무작위로 일렬로 배열된다. (a) 처음 5개의 공이 모두 파란색일 확률은 얼마인가? (b) 처음 5개의 공 중 파란색이 하나도 없을 확률은 얼마인가? (c) 마지막 3개의 공이 서로 다른 색깔일 확률은 얼마인가? (d) 모든 빨간 공이 함께 있을 확률은 얼마인가? 19. 4가지 다른 슈트 각각 13장씩 총 52장의 카드 덱에서 10장의 카드가 무작위로 선택된다. 선택된 각 카드는 슈트에 따라 4개의 더미 중 하나에 놓인다. (a) 가장 큰 더미에 4장, 다음으로 큰 더미에 3장, 그 다음 더미에 2장, 가장 작은 더미에 1장의 카드가 있을 확률은 얼마인가? (b) 두 더미에 각각 3장, 한 더미에 4장, 한 더미에 카드가 없을 확률은 얼마인가? 20. 처음에는 빨간 공 20개와 파란 공 10개가 들어있는 항아리에서 공이 무작위로 제거된다. 모든 빨간 공이 제거되기 전에 모든 파란 공이 제거될 확률은 얼마인가?

Chapter

Combinatorial Analysis

1

Contents

1.1 Introduction

1.2 The Basic Principle of Counting

The basic principle of counting

Example 2a

The generalized basic principle of counting

1.3 Permutations

Example 3a

Example 3f

1.4 Combinations

Notation and terminology

The binomial theorem

Example

Solution

1.5 Multinomial Coefficients

Notation

The multinomial theorem

Example 5d

Example 5e

*1.6 The Number of Integer Solutions of Equations

Example 6c

Example 6d

Solution

Summary

Problems

Theoretical Exercises

Hint:

Self-Test Problems and Exercises

Chapter

Axioms of Probability

Contents

2.1 Introduction

2.2 Sample Space and Events

2.3 Axioms of Probability

The three axioms of probability

Axiom 1

Axiom 2

Axiom 3

Example 3a

2.4 Some Simple Propositions

Proposition

Proposition

2.5 Sample Spaces Having Equally Likely Outcomes

Example 5a

Example 5b

Example 5f

Example 5i

Example <br> 5j

Example

Example 51

Example <br> 5m

The matching problem

*Example <br> 50

Runs

*2.6 Probability as a Continuous Set Function

Example 6a

Probability and a "paradox"

2.7 Probability as a Measure of Belief

Example

Summary

Problems

I: 10 percent I and II: 8 percent I and II and III: 1 percent

II: 30 percent I and III: 2 percent <br> III: 5 percent II and III: 4 percent

Theoretical Exercises

Self-Test Problems and Exercises