A First Course in Probability Chap3-4 중간고사 범위
A First Course in Probability Chap3-4 중간고사 범위
A-First-Course-in-Probability
Chapter
Conditional Probability and Independence
3
Contents
3.1 서론 3.2 조건부 확률 3.3 베이즈 공식 3.4 독립 사건 3.5 는 확률이다
3.1 Introduction
이 장에서는 확률 이론에서 가장 중요한 개념 중 하나인 **조건부 확률(conditional probability)**을 소개한다. 이 개념의 중요성은 두 가지이다. 첫째, 우리는 종종 실험 결과에 대한 부분적인 정보가 있을 때 확률을 계산하는 데 관심이 있다. 이러한 상황에서 원하는 확률은 조건부 확률이다. 둘째, 부분적인 정보가 없더라도 조건부 확률을 사용하여 원하는 확률을 더 쉽게 계산할 수 있는 경우가 많다.
3.2 Conditional Probabilities
2개의 주사위를 던지고, 가능한 36가지 결과 각각이 동일하게 발생할 가능성이 있으며 따라서 확률이 이라고 가정해 보자. 또한 첫 번째 주사위가 3이라는 것을 관찰했다고 가정해 보자. 이 정보가 주어졌을 때, 2개의 주사위 합이 8이 될 확률은 얼마일까? 이 확률을 계산하기 위해 다음과 같이 추론한다: 첫 번째 주사위가 3이라는 정보가 주어졌으므로, 우리 실험의 가능한 결과는 최대 6가지, 즉 , 그리고 이다. 이들 각각의 결과는 원래 동일한 발생 확률을 가졌으므로, 이 결과들은 여전히 동일한 확률을 가져야 한다. 즉, 첫 번째 주사위가 3이라는 정보가 주어졌을 때, , 그리고 각각의 (조건부) 확률은 이며, 표본 공간의 다른 30개 지점의 (조건부) 확률은 0이다. 따라서 원하는 확률은 이 될 것이다.
를 주사위 합이 8인 사건으로, 를 첫 번째 주사위가 3인 사건으로 각각 나타내면, 방금 얻은 확률은 가 발생했을 때 가 발생할 조건부 확률이라고 불리며 다음과 같이 표기된다.
모든 사건 와 에 유효한 에 대한 일반 공식은 동일한 방식으로 도출된다: 사건 가 발생했을 때, 가 발생하려면 실제 발생이 와 모두에 속하는 지점이어야 한다. 즉, 에 속해야 한다. 이제 가 발생했음을 알았으므로, 가 우리의 새로운, 또는 축소된 표본 공간이 된다. 따라서 사건 가 발생할 확률은 의 확률에 대한 의 확률과 같을 것이다. 즉, 다음과 같은 정의를 얻는다.
Definition
만약 이라면,
Example 2a
Joe는 잃어버린 열쇠가 걸려 있는 재킷의 두 주머니 중 하나에 있을 확률을 80%로 확신하며, 왼쪽 주머니에 있을 확률을 40%, 오른쪽 주머니에 있을 확률을 40%로 확신한다. 왼쪽 주머니를 찾아보았지만 열쇠를 찾지 못했다면, 열쇠가 다른 주머니에 있을 조건부 확률은 얼마인가?
풀이 열쇠가 재킷의 왼쪽 주머니에 있는 사건을 , 오른쪽 주머니에 있는 사건을 이라고 하면, 구하고자 하는 확률 는 다음과 같이 얻을 수 있다:
유한 표본 공간 의 각 결과가 동등하게 가능성 있는(equally likely) 경우, 결과가 부분집합 에 속한다는 사건을 조건으로 하면 내의 모든 결과는 동등하게 가능성 있게 된다. 이러한 경우, 를 표본 공간으로 사용하여 형태의 조건부 확률을 계산하는 것이 종종 편리하다. 실제로, 이 **축소된 표본 공간(reduced sample space)**으로 작업하면 더 쉽고 잘 이해되는 해결책을 얻을 수 있다. 다음 두 예시는 이 점을 보여준다.
Example
동전을 두 번 던진다. 표본 공간 의 네 가지 결과가 모두 동일하게 나올 가능성이 있다고 가정할 때, 다음 조건에서 두 번 모두 앞면이 나올 조건부 확률은 얼마인가? (a) 첫 번째 던지기에서 앞면이 나온 경우 (b) 적어도 한 번 앞면이 나온 경우
풀이 두 번 모두 앞면이 나오는 사건을 라고 하자. 첫 번째 던지기에서 앞면이 나오는 사건을 라고 하자. 적어도 한 번 앞면이 나오는 사건을 라고 하자.
(a)에 대한 확률은 다음으로부터 얻을 수 있다:
(b)의 경우, 다음을 얻는다:
따라서 첫 번째 던지기에서 앞면이 나왔을 때 두 번 모두 앞면이 나올 조건부 확률은 인 반면, 적어도 한 번 앞면이 나왔을 때 두 번 모두 앞면이 나올 조건부 확률은 에 불과하다. 많은 학생들은 처음에 이 후자의 결과에 놀라워한다. 그들은 적어도 한 번 앞면이 나왔다는 조건이 주어졌을 때, 두 가지 가능한 결과가 있다고 추론한다: 두 번 모두 앞면이 나오거나, 한 번만 앞면이 나오는 경우. 그러나 그들의 실수는 이 두 가지 가능성이 동일하게 나올 가능성이 있다고 가정하는 데 있다.
처음에는 4가지의 동일하게 나올 가능성이 있는 결과가 있다. 적어도 한 번 앞면이 나왔다는 정보는 결과가 가 아니라는 정보와 동일하므로, 우리는 의 3가지 동일하게 나올 가능성이 있는 결과를 남게 되며, 이 중 오직 하나만이 두 번 모두 앞면이 나오는 결과이다.
Example 2c
카드 게임 브리지에서 52장의 카드는 동, 서, 남, 북으로 불리는 4명의 플레이어에게 똑같이 분배된다. 만약 북과 남이 총 8장의 스페이드를 가지고 있다면, 동이 나머지 5장의 스페이드 중 3장을 가질 확률은 얼마인가?
해결 원하는 확률을 계산하는 가장 쉬운 방법은 **축소된 표본 공간(reduced sample space)**을 사용하는 것이다. 즉, 북-남이 26장의 카드 중 총 8장의 스페이드를 가지고 있다고 가정하면, 동-서의 패에 분배될 총 26장의 카드가 남게 되며, 이 중 정확히 5장이 스페이드이다. 각 분배가 동일하게 가능하므로, 동이 자신의 13장 카드 중 정확히 3장의 스페이드를 가질 조건부 확률은 다음과 같다.
\frac{\binom{5}{3}\binom{21}{10}}{\binom{26}{13}} \approx .339 $$ $\square$ 식 (2.1)의 양변에 $P(F)$를 곱하면 다음을 얻는다.P(E F)=P(F) P(E \mid F)
식 (2.2)는 **$E$와 $F$가 모두 발생할 확률은 $F$가 발생할 확률에 $F$가 발생했을 때 $E$의 조건부 확률을 곱한 것과 같다**는 것을 의미한다. 식 (2.2)는 사건의 교집합의 확률을 계산하는 데 종종 매우 유용하다. 예제 2d 셀린은 프랑스어 수업을 들을지 화학 수업을 들을지 결정하지 못하고 있다. 그녀는 프랑스어 수업에서 A 학점을 받을 확률은 $\frac{1}{2}$이고, 화학 수업에서 A 학점을 받을 확률은 $\frac{2}{3}$라고 예상한다. 만약 셀린이 공정한 동전 던지기로 결정을 내린다면, 그녀가 화학에서 A 학점을 받을 확률은 얼마인가? 해결 셀린이 화학 수업을 듣는 사건을 $C$라고 하고, 그녀가 어떤 수업을 듣든 A 학점을 받는 사건을 $A$라고 하자. 그러면 원하는 확률은 $P(C A)$이며, 이는 식 (2.2)를 사용하여 다음과 같이 계산된다.\begin{aligned} P(C A) & =P(C) P(A \mid C) \ & =\left(\frac{1}{2}\right)\left(\frac{2}{3}\right)=\frac{1}{3} \end{aligned}
## Example 2 e 항아리에 빨간 공 8개와 흰 공 4개가 들어 있다고 가정해 보자. 우리는 항아리에서 2개의 공을 비복원 추출한다. (a) 각 추출에서 항아리 안의 각 공이 선택될 확률이 동일하다고 가정할 때, 뽑힌 두 공이 모두 빨간색일 확률은 얼마인가? (b) 이제 공들이 서로 다른 무게를 가지고 있다고 가정해 보자. 각 빨간 공은 무게 $r$을 가지고, 각 흰 공은 무게 $w$를 가진다. 항아리 안의 특정 공이 다음으로 선택될 확률은 그 공의 무게를 현재 항아리 안의 모든 공의 무게 합으로 나눈 값이라고 가정해 보자. 이제 두 공이 모두 빨간색일 확률은 얼마인가? **풀이** $R_1$과 $R_2$를 각각 첫 번째와 두 번째로 뽑힌 공이 빨간색인 사건이라고 하자. 첫 번째로 선택된 공이 빨간색이라고 주어졌을 때, 남은 빨간 공은 7개이고 흰 공은 4개이므로, $P(R_2 \mid R_1) = \frac{7}{11}$이다. $P(R_1)$은 명백히 $\frac{8}{12}$이므로, 원하는 확률은 다음과 같다.\begin{aligned} P\left(R_{1} R_{2}\right) & =P\left(R_{1}\right) P\left(R_{2} \mid R_{1}\right) \ & =\left(\frac{2}{3}\right)\left(\frac{7}{11}\right)=\frac{14}{33} \end{aligned}
물론, 이 확률은 $P(R_1 R_2) = \binom{8}{2} / \binom{12}{2}$로 계산할 수도 있었다. (b) 부분에 대해서는 다시 $R_i$를 $i$번째로 선택된 공이 빨간색인 사건이라고 하고 다음을 사용한다.P\left(R_{1} R_{2}\right)=P\left(R_{1}\right) P\left(R_{2} \mid R_{1}\right)
이제 빨간 공들에 번호를 매기고, $B_i, i=1, \ldots, 8$을 첫 번째로 뽑힌 공이 $i$번 빨간 공인 사건이라고 하자. 그러면P\left(R_{1}\right)=P\left(\cup_{i=1}^{8} B_{i}\right)=\sum_{i=1}^{8} P\left(B_{i}\right)=8 \frac{r}{8 r+4 w}
P\left(R_{2} \mid R_{1}\right)=\frac{7 r}{7 r+4 w}
P\left(R_{1} R_{2}\right)=\frac{8 r}{8 r+4 w} \frac{7 r}{7 r+4 w}
P\left(E_{1} E_{2} E_{3} \cdots E_{n}\right)=P\left(E_{1}\right) P\left(E_{2} \mid E_{1}\right) P\left(E_{3} \mid E_{1} E_{2}\right) \cdots P\left(E_{n} \mid E_{1} \cdots E_{n-1}\right)
P\left(E_{1}\right) \frac{P\left(E_{1} E_{2}\right)}{P\left(E_{1}\right)} \frac{P\left(E_{1} E_{2} E_{3}\right)}{P\left(E_{1} E_{2}\right)} \cdots \frac{P\left(E_{1} E_{2} \cdots E_{n}\right)}{P\left(E_{1} E_{2} \cdots E_{n-1}\right)}=P\left(E_{1} E_{2} \cdots E_{n}\right)
**예제 2f** 2장 예제 5m에서 언급된 **매치 문제(match problem)**에서, $N$명의 사람들이 자신의 $N$개 모자 중에서 무작위로 선택할 때 **매치(match)**가 없는 확률 $P_N$은 다음과 같이 주어진다는 것이 보여졌다.P_{N}=\sum_{i=0}^{N}(-1)^{i} / i!
$N$명 중 정확히 $k$명이 매치를 가질 확률은 얼마인가? **풀이** 특정 $k$명의 사람들에게 주목하고, 이 $k$명의 개인이 매치를 가지고 다른 사람은 아무도 매치를 가지지 않을 확률을 결정해 보자. 이 집합의 모든 사람이 매치를 가지는 사건을 $E$라고 하고, 나머지 $N-k$명의 사람이 아무도 매치를 가지지 않는 사건을 $G$라고 하면, 우리는 다음을 얻는다.P(E G)=P(E) P(G \mid E)
이제, 집합의 $i$번째 구성원이 매치를 가지는 사건을 $F_i, i=1, \ldots, k$라고 하자. 그러면\begin{aligned} P(E) & =P\left(F_{1} F_{2} \cdots F_{k}\right) \ & =P\left(F_{1}\right) P\left(F_{2} \mid F_{1}\right) P\left(F_{3} \mid F_{1} F_{2}\right) \cdots P\left(F_{k} \mid F_{1} \cdots F_{k-1}\right) \ & =\frac{1}{N} \frac{1}{N-1} \frac{1}{N-2} \cdots \frac{1}{N-k+1} \ & =\frac{(N-k)!}{N!} \end{aligned}
$k$명으로 구성된 집합의 모든 사람이 매치를 가진다고 주어졌을 때, 나머지 $N-k$명의 사람들은 자신의 $N-k$개 모자 중에서 무작위로 선택할 것이므로, 그들 중 아무도 매치를 가지지 않을 확률은 $N-k$명의 사람들이 자신의 $N-k$개 모자 중에서 선택하는 문제에서 매치가 없는 확률과 같다. 따라서,P(G \mid E)=P_{N-k}=\sum_{i=0}^{N-k}(-1)^{i} / i!
이는 특정 $k$명의 사람들이 매치를 가지고 다른 사람은 아무도 매치를 가지지 않을 확률이 다음과 같음을 보여준다.P(E G)=\frac{(N-k)!}{N!} P_{N-k}
앞선 조건이 $k$명의 개인으로 구성된 $\binom{N}{k}$개의 집합 중 어느 하나에 대해 참이라면 정확히 $k$개의 매치가 있을 것이므로, 원하는 확률은 다음과 같다.\begin{aligned} P(\text { exactly } k \text { matches }) & =P_{N-k} / k! \ & \approx e^{-1} / k!\quad \text { when } N \text { is large } \end{aligned}
이제 곱셈 규칙을 사용하여 2장 예제 5h(b)를 푸는 두 번째 접근 방식을 얻을 것이다. **예제 2g** 52장의 일반적인 트럼프 카드가 각각 13장씩 4개의 더미로 무작위로 나뉜다. 각 더미에 정확히 1개의 에이스가 있을 확률을 계산하라. **풀이** 사건 $E_i, i=1,2,3,4$를 다음과 같이 정의한다.\begin{aligned} & E_{1}={\text { 스페이드 에이스가 더미 중 하나에 있다 }} \ & E_{2}={\text { 스페이드 에이스와 하트 에이스가 다른 더미에 있다 }} \ & E_{3}={\text { 스페이드, 하트, 다이아몬드 에이스가 모두 다른 더미에 있다 }} \ & E_{4}={\text { 4개의 에이스가 모두 다른 더미에 있다 }} \end{aligned}
원하는 확률은 $P(E_1 E_2 E_3 E_4)$이며, 곱셈 규칙에 의해,P\left(E_{1} E_{2} E_{3} E_{4}\right)=P\left(E_{1}\right) P\left(E_{2} \mid E_{1}\right) P\left(E_{3} \mid E_{1} E_{2}\right) P\left(E_{4} \mid E_{1} E_{2} E_{3}\right)
P\left(E_{1}\right)=1
왜냐하면 $E_1$은 표본 공간 $S$이기 때문이다. $P(E_2 \mid E_1)$을 결정하기 위해, 스페이드 에이스가 포함된 더미를 고려해 보자. 이 더미의 나머지 12장의 카드는 남은 51장의 카드 중 어떤 12장이라도 될 가능성이 동일하므로, 하트 에이스가 그 안에 있을 확률은 $12/51$이다. 따라서P\left(E_{2} \mid E_{1}\right)=1-\frac{12}{51}=\frac{39}{51}
또한, 스페이드 에이스와 하트 에이스가 다른 더미에 있다고 주어졌을 때, 이 두 더미의 나머지 24장의 카드 집합은 남은 50장의 카드 중 어떤 24장이라도 될 가능성이 동일하다. 다이아몬드 에이스가 이 24장 중 하나일 확률이 $24/50$이므로, 우리는 다음을 알 수 있다.P\left(E_{3} \mid E_{1} E_{2}\right)=1-\frac{24}{50}=\frac{26}{50}
P\left(E_{4} \mid E_{1} E_{2} E_{3}\right)=1-\frac{36}{49}=\frac{13}{49}
P\left(E_{1} E_{2} E_{3} E_{4}\right)=\frac{39 \cdot 26 \cdot 13}{51 \cdot 50 \cdot 49} \approx .105
즉, 각 더미에 에이스가 포함될 확률은 약 10.5%이다. (문제 13은 이 문제를 해결하기 위해 곱셈 규칙을 사용하는 또 다른 방법을 제시한다.) **비고** $P(E \mid F)$에 대한 우리의 정의는 확률을 **장기 상대 빈도(long-run relative frequency)**로 해석하는 것과 일치한다. 이를 이해하기 위해, $n$번의 실험 반복이 수행될 것이라고 가정해 보자. 여기서 $n$은 큰 숫자이다. 우리는 $F$가 발생하는 실험들만 고려한다면, $P(E \mid F)$가 $E$도 발생하는 실험들의 장기 비율과 같을 것이라고 주장한다. 이 진술을 확인하기 위해, $P(F)$가 $F$가 발생하는 실험들의 장기 비율이므로, $n$번의 실험 반복에서 $F$는 약 $n P(F)$번 발생할 것이라는 점에 주목하자. 유사하게, 이 실험들 중 약 $n P(E F)$번에서는 $E$와 $F$가 모두 발생할 것이다. 따라서 $F$가 발생하는 약 $n P(F)$번의 실험 중에서 $E$도 발생하는 비율은 대략 다음과 같다.\frac{n P(E F)}{n P(F)}=\frac{P(E F)}{P(F)}
이 근사치가 $n$이 점점 커질수록 정확해지므로, 우리는 $P(E \mid F)$에 대한 적절한 정의를 가지고 있다. ### 3.3 Bayes's Formula $E$와 $F$를 사건이라고 하자. 우리는 $E$를 다음과 같이 표현할 수 있다.E=E F \cup E F^{c}
이는 어떤 결과가 $E$에 속하려면, $E$와 $F$ 모두에 속하거나 $E$에는 속하지만 $F$에는 속하지 않아야 하기 때문이다. (그림 3.1 참조) $E F$와 $E F^{c}$는 분명히 **상호 배타적(mutually exclusive)**이므로, 공리 3에 의해 다음이 성립한다.\begin{aligned} P(E) & =P(E F)+P\left(E F^{c}\right) \ & =P(E \mid F) P(F)+P\left(E \mid F^{c}\right) P\left(F^{c}\right) \ & =P(E \mid F) P(F)+P\left(E \mid F^{c}\right)[1-P(F)] \end{aligned}
식 (3.1)은 사건 $E$의 확률이 $F$가 발생했을 때의 $E$의 **조건부 확률(conditional probability)**과 $F$가 발생하지 않았을 때의 $E$의 조건부 확률의 **가중 평균(weighted average)**임을 나타낸다. 각 조건부 확률은 조건이 되는 사건이 발생할 확률만큼의 가중치를 갖는다. 이 공식은 매우 유용하다. 왜냐하면 이 공식을 사용하면 종종 어떤 두 번째 사건이 발생했는지 여부에 먼저 **"조건화(conditioning)"**함으로써 사건의 확률을 결정할 수 있기 때문이다. 즉, 사건의 확률을 직접 계산하기는 어렵지만, 어떤 두 번째 사건이 발생했는지 여부를 알면 계산하기 쉬운 경우가 많다. 몇 가지 예시를 통해 이 아이디어를 설명한다. 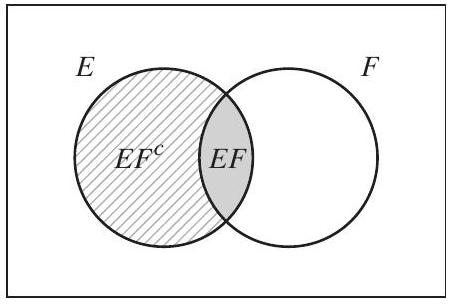 그림 3.1 $E=E F \cup E F^{c} . E F=$ 음영 영역; $E F^{c}=$ 줄무늬 영역. ## Example 3a ## (Part 1) 보험 회사는 사람들을 두 가지 부류로 나눌 수 있다고 생각한다: 사고를 잘 일으키는 사람(accident prone)과 그렇지 않은 사람. 회사 통계에 따르면, 사고를 잘 일으키는 사람은 고정된 1년 기간 내에 사고를 낼 확률이 .4인 반면, 사고를 잘 일으키지 않는 사람의 경우 이 확률은 .2로 감소한다. 만약 인구의 30%가 사고를 잘 일으키는 사람이라고 가정할 때, 새로운 보험 가입자가 보험 가입 후 1년 이내에 사고를 낼 확률은 얼마인가? 해결책 우리는 보험 가입자가 사고를 잘 일으키는 사람인지 아닌지에 따라 먼저 조건부 확률을 구하여 원하는 확률을 얻을 것이다. $A_1$을 보험 가입자가 보험 가입 후 1년 이내에 사고를 낼 사건이라고 하고, $A$를 보험 가입자가 사고를 잘 일으키는 사람일 사건이라고 하자. 따라서 원하는 확률은 다음과 같이 주어진다:\begin{aligned} P\left(A_{1}\right) & =P\left(A_{1} \mid A\right) P(A)+P\left(A_{1} \mid A^{c}\right) P\left(A^{c}\right) \ & =(.4)(.3)+(.2)(.7)=.26 \end{aligned}
## Example 3a ## (Part 2) 새로운 보험 가입자가 보험 가입 후 1년 이내에 사고를 냈다고 가정해 보자. 이 사람이 사고를 자주 내는 사람일 확률은 얼마인가? 풀이 원하는 확률은 다음과 같다.\begin{aligned} P\left(A \mid A_{1}\right) & =\frac{P\left(A A_{1}\right)}{P\left(A_{1}\right)} \ & =\frac{P(A) P\left(A_{1} \mid A\right)}{P\left(A_{1}\right)} \ & =\frac{(.3)(.4)}{.26}=\frac{6}{13} \end{aligned}
\frac{n-1}{n} \frac{1}{n-1}=\frac{1}{n}
\begin{aligned} P{\operatorname{win}} & =P{\operatorname{win} \mid G} P(G)+P\left{\operatorname{win} \mid G^{c}\right}(1-P(G))=\frac{1}{n} p+\frac{1}{n}(1-p) \ & =\frac{1}{n} \end{aligned}
\begin{aligned} P(K \mid C) & =\frac{P(K C)}{P(C)} \ & =\frac{P(C \mid K) P(K)}{P(C \mid K) P(K)+P\left(C \mid K^{c}\right) P\left(K^{c}\right)} \ & =\frac{p}{p+(1 / m)(1-p)} \ & =\frac{m p}{1+(m-1) p} \end{aligned}
\begin{aligned} P(D \mid E) & =\frac{P(D E)}{P(E)} \ & =\frac{P(E \mid D) P(D)}{P(E \mid D) P(D)+P\left(E \mid D^{c}\right) P\left(D^{c}\right)} \ & =\frac{(.95)(.005)}{(.95)(.005)+(.01)(.995)} \ & =\frac{95}{294} \approx .323 \end{aligned}
\frac{.95}{.95+(199)(.01)}=\frac{95}{294} \approx .323
식 (3.1)은 추가 정보에 비추어 개인적인 확률을 재평가해야 할 때도 유용하다. 예를 들어, 다음 예제들을 고려해 보자. ## Example 3e 한 의료인이 다음과 같은 딜레마에 빠져 있다고 가정해 보자: "환자가 이 질병을 앓고 있을 확률이 80% 이상이라고 확신하면 항상 수술을 권하지만, 그만큼 확신하지 못하면 비싸고 때로는 고통스러운 추가 검사를 권한다. 처음에는 존스가 이 질병을 앓고 있을 확률이 60%라고만 확신했기 때문에 A 검사를 지시했다. 이 검사는 환자가 질병을 앓고 있을 때는 항상 양성 결과를 보이고, 건강할 때는 거의 양성 결과를 보이지 않는다. 검사 결과는 양성이었고, 나는 수술을 권할 준비가 되어 있었는데, 존스가 처음으로 자신이 당뇨병 환자라고 알려주었다. 이 정보는 문제를 복잡하게 만드는데, 왜냐하면 이 정보가 존스가 해당 질병을 앓고 있을 확률에 대한 나의 원래 60% 추정치를 바꾸지는 않지만, A 검사 결과의 해석에는 영향을 미치기 때문이다. 이는 A 검사가 환자가 건강할 때는 결코 양성 결과를 보이지 않지만, 불행히도 질병을 앓고 있지 않은 당뇨병 환자의 경우 30%의 확률로 양성 결과를 보이기 때문이다. 이제 어떻게 해야 할까? 추가 검사인가, 아니면 즉시 수술인가?" 해결책 수술을 권할지 여부를 결정하기 위해 의사는 A 검사 결과가 양성이라는 점을 고려하여 존스가 질병을 앓고 있을 확률을 먼저 다시 계산해야 한다. $D$를 존스가 질병을 앓고 있는 사건이라고 하고, $E$를 A 검사 결과가 양성인 사건이라고 하자. 그러면 원하는 조건부 확률은 다음과 같다.\begin{aligned} P(D \mid E) & =\frac{P(D E)}{P(E)} \ & =\frac{P(D) P(E \mid D)}{P(E \mid D) P(D)+P\left(E \mid D^{c}\right) P\left(D^{c}\right)} \ & =\frac{(.6) 1}{1(.6)+(.3)(.4)} \ & =.833 \end{aligned}
우리는 존스가 질병을 앓고 있는지 여부에 따라 양성 검사 결과의 확률을 조건화한 다음, 존스가 당뇨병 환자이므로 질병을 앓고 있지 않을 때 양성 결과가 나올 조건부 확률 $P\left(E \mid D^{c}\right)$가 .3과 같다는 사실을 사용했다. 따라서 의사는 이제 존스가 질병을 앓고 있을 확률이 80% 이상이라고 확신해야 하므로 수술을 권해야 한다. $\square$ 예시 3f 범죄 수사의 특정 단계에서 담당 수사관은 특정 용의자의 유죄를 60% 확신하고 있다. 그러나 범인이 특정 특징(예: 왼손잡이, 대머리, 갈색 머리)을 가지고 있음을 보여주는 새로운 증거가 발견되었다고 가정해 보자. 인구의 20%가 이 특징을 가지고 있다면, 용의자가 그 특징을 가지고 있는 것으로 밝혀졌을 때 수사관은 용의자의 유죄를 얼마나 확신해야 할까? 해결책 $G$를 용의자가 유죄인 사건이라고 하고, $C$를 용의자가 범인의 특징을 가지고 있는 사건이라고 하면 다음과 같다.\begin{aligned} P(G \mid C) & =\frac{P(G C)}{P(C)} \ & =\frac{P(C \mid G) P(G)}{P(C \mid G) P(G)+P\left(C \mid G^{c}\right) P\left(G^{c}\right)} \ & =\frac{1(.6)}{1(.6)+(.2)(.4)} \ & \approx .882 \end{aligned}
여기서 용의자가 실제로 무죄일 경우 그 특징을 가질 확률은 그 특징을 가진 인구의 비율인 .2와 같다고 가정했다. 1965년 5월 부에노스아이레스에서 열린 세계 브리지 선수권 대회에서 유명한 영국 브리지 파트너십인 테렌스 리스(Terrence Reese)와 보리스 샤피로(Boris Schapiro)는 플레이어들이 가지고 있는 하트의 수를 나타낼 수 있는 손가락 신호 시스템을 사용하여 부정행위를 했다는 비난을 받았다. 리스와 샤피로는 이 비난을 부인했고, 결국 영국 브리지 리그에서 청문회가 열렸다. 청문회는 검찰과 변호인단이 모두 증인을 소환하고 반대 심문할 권한을 가진 법적 절차의 형태였다. 절차 과정에서 검사는 리스와 샤피로가 플레이한 특정 핸드를 조사하고, 이 핸드를 플레이한 것이 그들이 하트 슈트에 대한 불법적인 지식을 가지고 있었다는 가설과 일치한다고 주장했다. 이때 변호사는 그들의 핸드 플레이가 그들의 표준 플레이 방식과도 완벽하게 일치한다고 지적했다. 그러나 검찰은 그들의 플레이가 유죄 가설과 일치하는 한, 그 가설에 대한 증거로 간주되어야 한다고 주장했다. 검찰의 추론에 대해 어떻게 생각하는가? 해결책 이 문제는 기본적으로 새로운 증거(이 예에서는 핸드 플레이)의 도입이 특정 가설의 확률에 어떻게 영향을 미치는지 결정하는 문제이다. $H$를 특정 가설(예: 리스와 샤피로가 유죄라는 가설)이라고 하고 $E$를 새로운 증거라고 하면 다음과 같다.\begin{aligned} P(H \mid E) & =\frac{P(H E)}{P(E)} \ & =\frac{P(E \mid H) P(H)}{P(E \mid H) P(H)+P\left(E \mid H^{c}\right)[1-P(H)]} \end{aligned}
여기서 $P(H)$는 새로운 증거가 도입되기 전 가설의 가능성에 대한 우리의 평가이다. 새로운 증거는 가설을 더 가능성 있게 만들 때, 즉 $P(H \mid E) \geq P(H)$일 때 가설을 지지한다. 방정식 (3.2)에 따르면, 이는 다음과 같을 때 발생한다.P(E \mid H) \geq P(E \mid H) P(H)+P\left(E \mid H^{c}\right)[1-P(H)]
P(E \mid H) \geq P\left(E \mid H^{c}\right)
P(H \mid E)=\frac{P(H)}{P(H)+[1-P(H)] \frac{P\left(E \mid H^{c}\right)}{P(E \mid H)}}
따라서 고려 중인 문제에서 카드 플레이는 파트너십이 부정행위를 했을 때가 그렇지 않았을 때보다 그러한 플레이가 더 가능성이 높았을 경우에만 유죄 가설을 지지하는 것으로 간주될 수 있다. 검사는 이러한 주장을 한 적이 없으므로, 증거가 유죄 가설을 지지한다는 그의 주장은 유효하지 않다. ## Example <br> 3h 쌍둥이는 일란성 또는 이란성일 수 있다. **일란성(monozygotic)** 쌍둥이는 하나의 수정란이 두 개의 유전적으로 동일한 부분으로 분리될 때 형성된다. 결과적으로 일란성 쌍둥이는 항상 동일한 유전자 세트를 갖는다. **이란성(dizygotic)** 쌍둥이는 두 개의 난자가 수정되어 자궁에 착상될 때 발생한다. 이란성 쌍둥이의 유전적 연결은 다른 시기에 태어난 형제자매와 동일하다. 캘리포니아 로스앤젤레스 카운티의 한 과학자는 카운티에서 태어나는 쌍둥이 중 일란성 쌍둥이의 현재 비율을 알고 싶어 카운티 통계학자에게 이 문제를 연구하도록 지시했다. 통계학자는 처음에 카운티 내 각 병원에 모든 쌍둥이 출생 기록을 요청하고, 그 쌍둥이가 일란성인지 여부를 표시해달라고 요청했다. 그러나 병원 측은 신생아 쌍둥이가 일란성인지 여부를 판단하는 것이 간단한 작업이 아니라고 답했다. 이는 복잡하고 비용이 많이 드는 DNA 연구를 수행하기 위해 쌍둥이 부모의 허락이 필요하며, 병원에서는 그 비용을 감당할 수 없었기 때문이다. 고심 끝에 통계학자는 병원에 쌍둥이 출생 기록과 함께 쌍둥이가 **동성(same sex)**인지 여부를 나타내는 데이터만 요청했다. 이러한 데이터가 쌍둥이 출생의 약 64%가 동성임을 나타냈을 때, 통계학자는 전체 쌍둥이의 약 28%가 일란성이라고 선언했다. 그녀는 어떻게 이러한 결론에 도달했을까? **해결책** 통계학자는 **일란성 쌍둥이는 항상 동성**인 반면, **이란성 쌍둥이는 다른 형제자매와 동일한 관계를 가지므로 동성일 확률이 $1/2$**이라고 추론했다. 쌍둥이가 일란성일 사건을 $I$로, 쌍둥이가 동성일 사건을 $SS$로 두면, 그녀는 쌍둥이가 일란성인지 여부에 따라 조건부 확률을 사용하여 $P(SS)$를 계산했다. 이는 다음을 제공한다:P(S S)=P(S S \mid I) P(I)+P\left(S S \mid I^{c}\right) P\left(I^{c}\right)
P(S S)=1 \times P(I)+\frac{1}{2} \times[1-P(I)]=\frac{1}{2}+\frac{1}{2} P(I)
$P(SS) \approx .64$를 사용하면 다음 결과가 도출된다:P(I) \approx .28
새로운 증거가 도입될 때 가설의 확률 변화는 해당 가설의 **오즈(odds)** 변화로 간결하게 표현될 수 있으며, 오즈의 개념은 다음과 같이 정의된다. ## Definition 어떤 사건 $A$의 **odds**는 다음과 같이 정의된다.\frac{P(A)}{P\left(A^{c}\right)}=\frac{P(A)}{1-P(A)}
즉, 사건 $A$의 **odds**는 사건 $A$가 발생할 가능성이 발생하지 않을 가능성보다 얼마나 더 높은지를 나타낸다. 예를 들어, $P(A)=\frac{2}{3}$이면 $P(A)= 2 P\left(A^{c}\right)$이므로 **odds**는 2이다. **odds**가 $\alpha$와 같으면, 가설에 유리하게 "$\alpha$ 대 1"의 **odds**라고 흔히 말한다. 이제 확률 $P(H)$로 참인 가설 $H$를 고려하고, 새로운 증거 $E$가 도입되었다고 가정해 보자. 그러면 증거 $E$가 주어졌을 때, $H$가 참일 조건부 확률과 $H$가 참이 아닐 조건부 확률은 각각 다음과 같다.P(H \mid E)=\frac{P(E \mid H) P(H)}{P(E)} \quad P\left(H^{c} \mid E\right)=\frac{P\left(E \mid H^{c}\right) P\left(H^{c}\right)}{P(E)}
따라서 증거 $E$가 도입된 후의 새로운 **odds**는 다음과 같다.\frac{P(H \mid E)}{P\left(H^{c} \mid E\right)}=\frac{P(H)}{P\left(H^{c}\right)} \frac{P(E \mid H)}{P\left(E \mid H^{c}\right)}
즉, $H$의 **odds**의 새로운 값은 이전 값에, $H$가 참일 때 새로운 증거의 조건부 확률과 $H$가 참이 아닐 때의 조건부 확률의 비율을 곱한 것이다. 따라서 식 (3.3)은 예제 3f의 결과를 검증한다. 왜냐하면 새로운 증거가 $H$가 거짓일 때보다 참일 때 더 가능성이 높으면 **odds**, 그리고 $H$의 확률이 증가하기 때문이다. 마찬가지로, 새로운 증거가 $H$가 참일 때보다 거짓일 때 더 가능성이 높으면 **odds**는 감소한다. ## Example 항아리에는 두 개의 **type A** 동전과 한 개의 **type B** 동전이 들어 있다. **type A** 동전을 뒤집으면 $1/4$의 확률로 앞면이 나오고, **type B** 동전을 뒤집으면 $3/4$의 확률로 앞면이 나온다. 항아리에서 무작위로 동전 하나를 선택하여 뒤집었다. 뒤집은 결과 앞면이 나왔을 때, 이 동전이 **type A** 동전이었을 확률은 얼마인가? 풀이 **type A** 동전이 뒤집힌 사건을 $A$라고 하고, **type B** 동전이 뒤집힌 사건을 $B=A^c$라고 하자. 우리는 $P(A \mid \text{heads})$를 구하고자 한다. 여기서 **heads**는 뒤집은 결과 앞면이 나온 사건이다. 식 (3.3)에서 다음을 알 수 있다.\begin{aligned} \frac{P(A \mid \text { heads })}{P\left(A^{c} \mid \text { heads }\right)} & =\frac{P(A)}{P(B)} \frac{P(\text { heads } \mid A)}{P(\text { heads } \mid B)} \ & =\frac{2 / 3}{1 / 3} \frac{1 / 4}{3 / 4} \ & =2 / 3 \end{aligned}
따라서 **odds**는 $2/3:1$이며, 이는 **type A** 동전이 뒤집혔을 확률이 $2/5$와 동일하다. 식 (3.1)은 다음과 같이 일반화될 수 있다: $F_1, F_2, \ldots, F_n$이 **상호 배타적인 사건(mutually exclusive events)**이고 다음을 만족한다고 가정하자.\bigcup_{i=1}^{n} F_{i}=S
다시 말해, 사건 $F_1, F_2, \ldots, F_n$ 중 정확히 하나만 발생해야 한다. 다음을 작성하고E=\bigcup_{i=1}^{n} E F_{i}
사건 $E F_i, i=1, \ldots, n$이 **상호 배타적**이라는 사실을 사용하면 다음을 얻는다.\begin{aligned} P(E) & =\sum_{i=1}^{n} P\left(E F_{i}\right) \ & =\sum_{i=1}^{n} P\left(E \mid F_{i}\right) P\left(F_{i}\right) \end{aligned}
따라서 종종 **전확률의 법칙(law of total probability)**이라고 불리는 식 (3.4)는 $F_1, F_2, \ldots, F_n$ 중 하나만 발생해야 하는 주어진 사건들에 대해, $F_i$ 중 어떤 사건이 발생하는지에 먼저 **조건화(conditioning)**함으로써 $P(E)$를 계산하는 방법을 보여준다. 즉, 식 (3.4)는 $P(E)$가 $P(E \mid F_i)$의 **가중 평균(weighted average)**과 같으며, 각 항은 조건화된 사건의 확률에 의해 가중된다는 것을 나타낸다. ## Example 3 j 2장 예제 5j에서 우리는 무작위로 섞인 카드 덱에서 첫 번째 에이스 다음에 특정 카드가 나올 확률을 고려했고, 이 확률이 $\frac{1}{52}$임을 보이기 위해 조합론적 논증을 제시했다. 다음은 **조건부 확률**에 기반한 확률론적 논증이다: 첫 번째 에이스 다음에 특정 카드, 예를 들어 카드 $x$가 나오는 사건을 $E$라고 하자. $P(E)$를 계산하기 위해 우리는 카드 $x$를 무시하고 덱에 있는 다른 51개 카드의 상대적 순서에 대해 조건화한다. $\mathbf{O}$를 순서라고 하면 다음과 같다.P(E)=\sum_{\mathbf{O}} P(E \mid \mathbf{O}) P(\mathbf{O})
이제 $\mathbf{O}$가 주어졌을 때, 카드 $x$가 덱에서 $i$번째 카드($i=1, \ldots, 52$)가 되는 것에 해당하는 52가지 가능한 카드 순서가 있다. 그러나 처음에는 52!가지 가능한 모든 순서가 동일하게 가능했으므로, $\mathbf{O}$가 주어졌을 때 나머지 52가지 가능한 순서 각각은 동일하게 가능하다. 카드 $x$는 이 순서 중 단 하나에서만 첫 번째 에이스 다음에 오므로, $P(E \mid \mathbf{O})=1 / 52$이고, 이는 $P(E)=1 / 52$임을 의미한다. 다시, $F_{1}, \ldots, F_{n}$을 **상호 배타적이고 전체를 포함하는 사건(mutually exclusive and exhaustive events)** 집합이라고 하자(즉, 이 사건들 중 정확히 하나만 발생해야 한다). 이제 $E$가 발생했고, 우리는 $F_{j}$ 중 어떤 것이 함께 발생했는지 결정하는 데 관심이 있다고 가정하자. 그러면 방정식 (3.4)에 따라 다음 명제를 얻는다. ## Proposition 3.1\begin{aligned} P\left(F_{j} \mid E\right) & =\frac{P\left(E F_{j}\right)}{P(E)} \ & =\frac{P\left(E \mid F_{j}\right) P\left(F_{j}\right)}{\sum_{i=1}^{n} P\left(E \mid F_{i}\right) P\left(F_{i}\right)} \end{aligned}
식 (3.5)는 영국의 철학자 Thomas Bayes의 이름을 따서 **Bayes의 공식**으로 알려져 있다. 만약 사건 $F_{j}$를 어떤 주제에 대한 가능한 "**가설**"이라고 생각한다면, Bayes의 공식은 실험이 수행되기 전에 이러한 가설에 대해 가지고 있던 의견[즉, $P\left(F_{j}\right)$]이 실험을 통해 얻은 증거에 의해 어떻게 수정되어야 하는지를 보여주는 것으로 해석될 수 있다. 비행기 한 대가 실종되었고, 3개의 가능한 지역 중 어느 한 곳에 추락했을 확률이 동일하다고 가정한다. $1-\beta_{i}, i=1,2,3$는 비행기가 실제로 $i$번째 지역에 있을 때, 해당 지역을 수색하여 비행기를 찾을 확률을 나타낸다. (상수 $\beta_{i}$는 **간과 확률(overlook probabilities)**이라고 불리는데, 이는 비행기를 간과할 확률을 나타내기 때문이다. 이 확률은 일반적으로 해당 지역의 지리적 및 환경적 조건에 기인한다.) 지역 1에 대한 수색이 실패했을 때, 비행기가 $i$번째 지역에 있을 조건부 확률은 얼마인가? 해답 $R_{i}, i=1,2,3$를 비행기가 $i$번째 지역에 있는 사건이라고 하고, $E$를 지역 1에 대한 수색이 실패한 사건이라고 하자. Bayes의 공식으로부터 다음을 얻는다.\begin{aligned} P\left(R_{1} \mid E\right) & =\frac{P\left(E R_{1}\right)}{P(E)} \ & =\frac{P\left(E \mid R_{1}\right) P\left(R_{1}\right)}{\sum_{i=1}^{3} P\left(E \mid R_{i}\right) P\left(R_{i}\right)} \ & =\frac{\left(\beta_{1}\right) \frac{1}{3}}{\left(\beta_{1}\right) \frac{1}{3}+(1) \frac{1}{3}+(1) \frac{1}{3}} \ & =\frac{\beta_{1}}{\beta_{1}+2} \end{aligned}
$j=2,3$에 대해,\begin{aligned} P\left(R_{j} \mid E\right) & =\frac{P\left(E \mid R_{j}\right) P\left(R_{j}\right)}{P(E)} \ & =\frac{(1) \frac{1}{3}}{\left(\beta_{1}\right) \frac{1}{3}+\frac{1}{3}+\frac{1}{3}} \ & =\frac{1}{\beta_{1}+2} \quad j=2,3 \end{aligned}
지역 1에 대한 수색에서 비행기를 찾지 못했다는 정보가 주어졌을 때, 비행기가 지역 $j$에 있을 **갱신된(즉, 조건부) 확률**은 $j \neq 1$일 때 초기 확률보다 크고, $j=1$일 때 초기 확률보다 작다는 점에 주목하라. 이 진술은 분명히 직관적이다. 왜냐하면 지역 1에서 비행기를 찾지 못했다는 것은 그 지역에 비행기가 있을 가능성을 감소시키고 다른 곳에 있을 가능성을 증가시키는 것으로 보이기 때문이다. 또한, 해당 지역에 대한 수색이 실패했을 때 비행기가 지역 1에 있을 조건부 확률은 간과 확률 $\beta_{1}$의 증가 함수이다. 이 진술 또한 직관적이다. $\beta_{1}$이 클수록, 비행기가 그곳에 없기 때문이라기보다는 "불운" 때문에 수색이 실패했다고 생각하는 것이 더 합리적이기 때문이다. 유사하게, $P\left(R_{j} \mid E\right), j \neq 1$는 $\beta_{1}$의 감소 함수이다. 다음 예시는 종종 부도덕한 확률론 학생들이 덜 깨달은 친구들로부터 돈을 따기 위해 사용해 왔다. ## Example 31 형태는 동일하지만, 첫 번째 카드의 양면은 빨간색, 두 번째 카드의 양면은 검은색, 세 번째 카드는 한 면이 빨간색이고 다른 면이 검은색으로 칠해진 3장의 카드가 있다고 가정해 보자. 이 3장의 카드를 모자 안에 섞어 넣고, 1장의 카드를 무작위로 선택하여 바닥에 놓는다. 선택된 카드의 윗면이 빨간색일 때, 다른 면이 검은색일 확률은 얼마인가? 풀이 선택된 카드가 모두 빨간색, 모두 검은색, 또는 빨간색-검은색 카드인 사건을 각각 $R R, B B$, 그리고 $R B$라고 하자. 또한, 선택된 카드의 윗면이 빨간색인 사건을 $R$이라고 하자. 그러면, 우리가 구하고자 하는 확률은 다음과 같이 얻어진다:\begin{aligned} P(R B \mid R) & =\frac{P(R B \cap R)}{P(R)} \ & =\frac{P(R \mid R B) P(R B)}{P(R \mid R R) P(R R)+P(R \mid R B) P(R B)+P(R \mid B B) P(B B)} \ & =\frac{\left(\frac{1}{2}\right)\left(\frac{1}{3}\right)}{(1)\left(\frac{1}{3}\right)+\left(\frac{1}{2}\right)\left(\frac{1}{3}\right)+0\left(\frac{1}{3}\right)}=\frac{1}{3} \end{aligned}
따라서 답은 $\frac{1}{3}$이다. 일부 학생들은 빨간색 면이 나타났을 때, 카드가 모두 빨간색 카드이거나 빨간색-검은색 카드일 두 가지 가능성이 동일하게 발생한다고 잘못 추론하여 답을 $\frac{1}{2}$로 추측한다. 그러나 그들의 실수는 이 두 가지 가능성이 동일하게 발생한다고 가정한 데 있다. 각 카드를 두 개의 다른 면으로 구성되어 있다고 생각하면, 실험의 6가지 동일하게 발생할 수 있는 결과, 즉 $R_{1}, R_{2}, B_{1}, B_{2}, R_{3}, B_{3}$가 있음을 알 수 있다. 여기서 결과는 모두 빨간색 카드의 첫 번째 면이 위로 향하면 $R_{1}$, 모두 빨간색 카드의 두 번째 면이 위로 향하면 $R_{2}$, 빨간색-검은색 카드의 빨간색 면이 위로 향하면 $R_{3}$ 등으로 정의된다. 윗면이 빨간색인 카드의 다른 면이 검은색이 되는 경우는 결과가 $R_{3}$일 때뿐이므로, 우리가 구하고자 하는 확률은 $R_{1}$ 또는 $R_{2}$ 또는 $R_{3}$가 발생했을 때 $R_{3}$의 조건부 확률이며, 이는 명백히 $\frac{1}{3}$과 같다. 예제 3m 두 자녀가 있는 것으로 알려진 신혼부부가 마을로 이사 왔다. 어머니가 자녀 중 한 명과 함께 걷고 있는 것을 만났다고 가정해 보자. 이 아이가 딸이라면, 두 자녀 모두 딸일 확률은 얼마인가? 풀이 다음 사건들을 정의하는 것부터 시작하자: $G_{1}$ : 첫째 (즉, 가장 나이가 많은) 아이는 딸이다. $G_{2}$ : 둘째 아이는 딸이다. $G$ : 어머니와 함께 있는 아이는 딸이다. 또한, $B_{1}, B_{2}$, 그리고 $B$는 "딸"이 "아들"로 대체된 유사한 사건들을 나타낸다. 이제 우리가 구하고자 하는 확률은 $P\left(G_{1} G_{2} \mid G\right)$이며, 이는 다음과 같이 표현될 수 있다:\begin{aligned} P\left(G_{1} G_{2} \mid G\right) & =\frac{P\left(G_{1} G_{2} G\right)}{P(G)} \ & =\frac{P\left(G_{1} G_{2}\right)}{P(G)} \end{aligned}
\begin{aligned} P(G)= & P\left(G \mid G_{1} G_{2}\right) P\left(G_{1} G_{2}\right)+P\left(G \mid G_{1} B_{2}\right) P\left(G_{1} B_{2}\right) \ & +P\left(G \mid B_{1} G_{2}\right) P\left(B_{1} G_{2}\right)+P\left(G \mid B_{1} B_{2}\right) P\left(B_{1} B_{2}\right) \ = & P\left(G_{1} G_{2}\right)+P\left(G \mid G_{1} B_{2}\right) P\left(G_{1} B_{2}\right)+P\left(G \mid B_{1} G_{2}\right) P\left(B_{1} G_{2}\right) \end{aligned}
여기서 마지막 방정식은 $P\left(G \mid G_{1} G_{2}\right)=1$과 $P\left(G \mid B_{1} B_{2}\right)=0$의 결과를 사용했다. 이제 4가지 성별 가능성이 모두 동일하게 발생한다고 가정하면, 다음과 같이 된다:\begin{aligned} P\left(G_{1} G_{2} \mid G\right) & =\frac{\frac{1}{4}}{\frac{1}{4}+P\left(G \mid G_{1} B_{2}\right) / 4+P\left(G \mid B_{1} G_{2}\right) / 4} \ & =\frac{1}{1+P\left(G \mid G_{1} B_{2}\right)+P\left(G \mid B_{1} G_{2}\right)} \end{aligned}
따라서 답은 사건 $G_{1} B_{2}$가 주어졌을 때 어머니와 함께 있는 아이가 딸일 조건부 확률과 사건 $G_{2} B_{1}$이 주어졌을 때 어머니와 함께 있는 아이가 딸일 조건부 확률에 대해 우리가 어떤 가정을 하느냐에 달려 있다. 예를 들어, 한편으로 자녀의 성별과 관계없이 어머니와 함께 걷는 아이가 어떤 확률 $p$로 첫째 아이일 것이라고 가정한다면, 다음과 같이 된다:P\left(G \mid G_{1} B_{2}\right)=p=1-P\left(G \mid B_{1} G_{2}\right)
P\left(G_{1} G_{2} \mid G\right)=\frac{1}{2}
다른 한편으로, 자녀의 성별이 다를 경우 어머니가 출생 순서와 관계없이 확률 $q$로 딸과 함께 걷는다고 가정한다면, 다음과 같이 된다:P\left(G \mid G_{1} B_{2}\right)=P\left(G \mid B_{1} G_{2}\right)=q
P\left(G_{1} G_{2} \mid G\right)=\frac{1}{1+2 q}
예를 들어, $q=1$이라고 가정하면, 즉 어머니가 항상 딸과 함께 걷는다는 의미라면, 두 딸을 가질 조건부 확률은 $\frac{1}{3}$이 된다. 이는 어머니가 딸과 함께 있는 것을 보는 것이 적어도 한 명의 딸을 가졌다는 사건과 동일하기 때문에 예제 2b와 일치한다. 따라서, 명시된 대로 이 문제는 해결할 수 없다. 실제로, 성별 확률이 동일하게 발생한다는 일반적인 가정을 하더라도, 해결책을 제시하기 위해서는 추가적인 가정이 필요하다. 이는 실험의 표본 공간이 $s_{1}, s_{2}, i$ 형태의 벡터로 구성되기 때문이다. 여기서 $s_{1}$은 첫째 아이의 성별, $s_{2}$는 둘째 아이의 성별, 그리고 $i$는 어머니와 함께 있는 아이의 출생 순서를 나타낸다. 결과적으로, 표본 공간의 사건들의 확률을 명시하기 위해서는 자녀의 성별에 대해서만 가정을 하는 것으로는 충분하지 않다. 자녀의 성별이 주어졌을 때 어떤 아이가 어머니와 함께 있는지에 대한 조건부 확률에 대해서도 가정을 해야 한다. ## Example 3n 예제 30 한 통에 3가지 종류의 일회용 손전등이 들어 있다. 1번 유형의 손전등이 100시간 이상 사용될 확률은 .7이고, 2번 유형과 3번 유형의 손전등에 대한 해당 확률은 각각 .4와 .3이다. 통에 있는 손전등 중 20%가 1번 유형, 30%가 2번 유형, 50%가 3번 유형이라고 가정하자. (a) 무작위로 선택된 손전등이 100시간 이상 사용될 확률은 얼마인가? (b) 손전등이 100시간 이상 지속되었다고 할 때, 그것이 $j$번 유형의 손전등일 조건부 확률은 얼마인가? ($j=1,2,3$) 풀이 (a) 선택된 손전등이 100시간 이상 사용될 사건을 $A$라고 하고, $j$번 유형의 손전등이 선택될 사건을 $F_j$라고 하자 ($j=1,2,3$). $P(A)$를 계산하기 위해 손전등의 유형에 따라 조건화하면 다음과 같다.\begin{aligned} P(A) & =P\left(A \mid F_{1}\right) P\left(F_{1}\right)+P\left(A \mid F_{2}\right) P\left(F_{2}\right)+P\left(A \mid F_{3}\right) P\left(F_{3}\right) \ & =(.7)(.2)+(.4)(.3)+(.3)(.5)=.41 \end{aligned}
\begin{aligned} P\left(F_{j} \mid A\right) & =\frac{P\left(A F_{j}\right)}{P(A)} \ & =\frac{P\left(A \mid F_{j}\right) P\left(F_{j}\right)}{.41} \end{aligned}
\begin{aligned} & P\left(F_{1} \mid A\right)=(.7)(.2) / .41=14 / 41 \ & P\left(F_{2} \mid A\right)=(.4)(.3) / .41=12 / 41 \ & P\left(F_{3} \mid A\right)=(.3)(.5) / .41=15 / 41 \end{aligned}
예를 들어, 1번 유형의 손전등이 선택될 초기 확률은 .2에 불과하지만, 손전등이 100시간 이상 지속되었다는 정보는 이 사건의 확률을 $14/41 \approx .341$로 높인다. 한 명의 개인이 범죄를 저질렀고, 범죄 현장에 DNA를 남겼다. 회수된 DNA를 연구한 법의학자들은 5개의 가닥만 식별할 수 있었고, 각 무고한 사람은 독립적으로 5개 가닥 모두에서 DNA가 일치할 확률이 $10^{-5}$임을 확인했다. 지방 검사는 마을의 100만 명 주민 중 누구라도 범죄의 가해자일 수 있다고 가정한다. 이 주민들 중 1만 명은 지난 10년 이내에 교도소에서 출소했으며, 따라서 그들의 DNA 샘플이 파일에 보관되어 있다. DNA 파일을 확인하기 전에 지방 검사는 1만 명의 전과자 각각이 새로운 범죄의 유죄일 확률이 $\alpha$이고, 나머지 99만 명의 주민 각각은 확률이 $\beta$라고 생각하며, 여기서 $\alpha=c\beta$이다. (즉, 지방 검사는 최근 출소한 각 수감자가 최근 출소한 수감자가 아닌 각 마을 구성원보다 $c$배 더 범죄의 가해자일 가능성이 높다고 가정한다.) 분석된 DNA를 1만 명의 전과자 데이터베이스와 비교한 결과, A. J. Jones만이 DNA 프로필과 일치하는 것으로 나타났다. 지방 검사의 $\alpha$와 $\beta$ 사이의 관계 추정치가 정확하다고 가정할 때, A. J.가 유죄일 확률은 얼마인가? 풀이 먼저, 확률의 합은 1이 되어야 하므로 다음을 얻는다.1=10,000 \alpha+990,000 \beta=(10,000 c+990,000) \beta
\beta=\frac{1}{10,000 c+990,000}, \quad \alpha=\frac{c}{10,000 c+990,000}
이제 A. J.가 유죄인 사건을 $G$라고 하고, A. J.가 파일에 있는 1만 명 중 유일하게 일치하는 사건을 $M$이라고 하자. 그러면,\begin{aligned} P(G \mid M) & =\frac{P(G M)}{P(M)} \ & =\frac{P(G) P(M \mid G)}{P(M \mid G) P(G)+P\left(M \mid G^{c}\right) P\left(G^{c}\right)} \end{aligned}
P(M \mid G)=\left(1-10^{-5}\right)^{9999}
다른 한편, A. J.가 무고하다면, 그가 유일한 일치자가 되기 위해서는 그의 DNA가 일치해야 하고 (확률 $10^{-5}$로 발생), 데이터베이스의 다른 모든 사람들은 무고해야 하며, 이들 중 누구도 일치하지 않아야 한다. 이제 A. J.가 무고하다고 가정할 때, 데이터베이스의 다른 모든 사람들도 무고할 조건부 확률은 다음과 같다.\begin{aligned} P(\text { all others innocent } \mid A J \text { innocent }) & =\frac{P(\text { all in database innocent })}{P(A J \text { innocent })} \ & =\frac{1-10,000 \alpha}{1-\alpha} \end{aligned}
또한, 데이터베이스의 다른 사람들이 무고하다고 가정할 때, 그들 중 누구도 일치하지 않을 조건부 확률은 $\left(1-10^{-5}\right)^{9999}$이다. 따라서,P\left(M \mid G^{c}\right)=10^{-5}\left(\frac{1-10,000 \alpha}{1-\alpha}\right)\left(1-10^{-5}\right)^{9999}
$P(G)=\alpha$이므로, 앞선 공식은 다음을 제공한다.P(G \mid M)=\frac{\alpha}{\alpha+10^{-5}(1-10,000 \alpha)}=\frac{1}{.9+\frac{10^{-5}}{\alpha}}
따라서, 지방 검사의 초기 생각이 임의의 전과자가 비전과자보다 범죄를 저지를 가능성이 100배 더 높다고 가정했다면 ($c=100$), $\alpha=\frac{1}{19,900}$이고P(G \mid M)=\frac{1}{1.099} \approx 0.9099
지방 검사가 초기 적절한 비율이 $c=10$이라고 생각했다면, $\alpha=\frac{1}{109,000}$이고P(G \mid M)=\frac{1}{1.99} \approx 0.5025
지방 검사가 초기 범죄자가 마을 구성원 중 누구라도 동일한 가능성을 가진다고 생각했다면 ($c=1$), $\alpha=10^{-6}$이고P(G \mid M)=\frac{1}{10.9} \approx 0.0917
따라서, 지방 검사의 초기 가정이 모든 인구 구성원이 범죄자일 가능성이 동일하다고 할 때 약 9%에서, 각 전과자가 전과자가 아닌 특정 마을 사람보다 범죄자일 가능성이 100배 더 높다고 가정할 때 약 91%까지 확률이 달라진다. ### 3.4 Independent Events 이 장의 이전 예시들은 $F$가 주어졌을 때 $E$의 조건부 확률인 $P(E \mid F)$가 일반적으로 $E$의 무조건부 확률인 $P(E)$와 같지 않음을 보여준다. 다시 말해, $F$가 발생했다는 것을 아는 것은 일반적으로 $E$의 발생 가능성을 변화시킨다. **$P(E \mid F)$가 실제로 $P(E)$와 같은 특별한 경우에, 우리는 $E$가 $F$에 독립이라고 말한다.** 즉, $E$가 $F$에 독립이라는 것은 $F$가 발생했다는 지식이 $E$가 발생할 확률을 변화시키지 않는다는 의미이다. $P(E \mid F)=P(E F) / P(F)$이므로, $E$가 $F$에 독립이라면 다음이 성립한다:P(E F)=P(E) P(F)
식 (4.1)이 $E$와 $F$에 대해 대칭적이라는 사실은 $E$가 $F$에 독립일 때마다 $F$도 $E$에 독립임을 보여준다. 따라서 우리는 다음 정의를 갖는다. ## Definition 두 사건 $E$와 $F$는 방정식 (4.1)이 성립할 때 **독립(independent)**이라고 한다. 독립이 아닌 두 사건 $E$와 $F$는 **종속(dependent)**이라고 한다. 예제 4a 52장의 일반적인 트럼프 카드 덱에서 무작위로 한 장의 카드를 선택한다. 선택된 카드가 에이스인 사건을 $E$, 스페이드인 사건을 $F$라고 하면, $E$와 $F$는 독립이다. 이는 $P(E F)=\frac{1}{52}$인 반면, $P(E)=\frac{4}{52}$이고 $P(F)=\frac{13}{52}$이기 때문이다. 예제 4b 두 개의 동전을 던지고, 4가지 결과가 모두 동일하게 나올 가능성이 있다고 가정한다. 첫 번째 동전이 앞면이 나오는 사건을 $E$, 두 번째 동전이 뒷면이 나오는 사건을 $F$라고 하면, $E$와 $F$는 독립이다. 왜냐하면 $P(E F)=P(\{(H, T)\})=\frac{1}{4}$인 반면, $P(E)=P(\{(H, H),(H, T)\})=\frac{1}{2}$이고 $P(F)=P(\{(H, T),(T, T)\})=\frac{1}{2}$이기 때문이다. 예제 4c 두 개의 공정한 주사위를 던진다고 가정하자. 주사위의 합이 6인 사건을 $E_{1}$이라고 하고, 첫 번째 주사위가 4인 사건을 $F$라고 하자. 그러면P\left(E_{1} F\right)=P({(4,2)})=\frac{1}{36}
P\left(E_{1}\right) P(F)=\left(\frac{5}{36}\right)\left(\frac{1}{6}\right)=\frac{5}{216}
이다. 따라서 $E_{1}$과 $F$는 독립이 아니다. 직관적으로 그 이유는 명확하다. 두 주사위의 합이 6이 될 가능성에 관심이 있다면, 첫 번째 주사위가 4 (또는 실제로 1, 2, 3, 4, 5 중 어떤 숫자라도)가 나오면 우리는 매우 기쁠 것이다. 왜냐하면 여전히 합이 6이 될 가능성이 남아있기 때문이다. 그러나 첫 번째 주사위가 6이 나온다면, 우리는 더 이상 합이 6이 될 기회가 없으므로 불행할 것이다. 다시 말해, 합이 6이 될 가능성은 첫 번째 주사위의 결과에 따라 달라진다. 따라서 $E_{1}$과 $F$는 독립일 수 없다. 이제 주사위의 합이 7인 사건을 $E_{2}$라고 가정하자. $E_{2}$는 $F$와 독립일까? 답은 '그렇다'이다. 왜냐하면P\left(E_{2} F\right)=P({(4,3)})=\frac{1}{36}
P\left(E_{2}\right) P(F)=\left(\frac{1}{6}\right)\left(\frac{1}{6}\right)=\frac{1}{36}
이기 때문이다. 주사위의 합이 7인 사건이 첫 번째 주사위의 결과와 독립인 이유에 대한 직관적인 설명을 독자가 제시하도록 남겨둔다. ## Example 4d 다음 대통령이 공화당원일 사건을 $E$로, 내년에 큰 지진이 발생할 사건을 $F$로 둔다면, 대부분의 사람들은 아마도 $E$와 $F$가 **독립적**이라고 기꺼이 가정할 것이다. 그러나 $E$가 $G$와 독립적이라고 가정하는 것이 합리적인지에 대해서는 논란이 있을 수 있다. 여기서 $G$는 선거 후 2년 이내에 경기 침체가 발생할 사건이다. 이제 $E$가 $F$와 독립이면 $E$는 $F^{c}$와도 독립임을 보인다. 명제 $E$와 $F$가 독립이면 $E$와 $F^{c}$도 독립이다. 4.1 증명 $E$와 $F$가 독립이라고 가정하자. $E=E F \cup E F^{c}$이고 $E F$와 $E F^{c}$는 분명히 상호 배타적이므로, 다음이 성립한다.\begin{aligned} P(E) & =P(E F)+P\left(E F^{c}\right) \ & =P(E) P(F)+P\left(E F^{c}\right) \end{aligned}
\begin{aligned} P\left(E F^{c}\right) & =P(E)[1-P(F)] \ & =P(E) P\left(F^{c}\right) \end{aligned}
이로써 결과가 증명된다. 따라서 $E$가 $F$와 독립이면, $F$의 발생 여부에 대한 정보는 $E$의 발생 확률을 변화시키지 않는다. 이제 $E$가 $F$와 독립이고 $G$와도 독립이라고 가정해보자. 그렇다면 $E$는 $F G$와도 반드시 독립일까? 다음 예시가 보여주듯이, 다소 놀랍게도 답은 '아니오'이다. 예시 4e 두 개의 공정한 주사위를 던진다. 주사위 눈의 합이 7인 사건을 $E$로 두자. 첫 번째 주사위 눈이 4인 사건을 $F$로, 두 번째 주사위 눈이 3인 사건을 $G$로 두자. 예시 4c에서 우리는 $E$가 $F$와 독립임을 알고 있으며, 동일한 추론을 적용하면 $E$가 $G$와도 독립임을 알 수 있다. 그러나 $E$는 $F G$와 분명히 독립이 아니다($P(E \mid F G)=1$이므로). 예시 4e로부터 세 사건 $E, F, G$의 독립성에 대한 적절한 정의는 단순히 $\binom{3}{2}$개의 모든 사건 쌍이 독립이라고 가정하는 것 이상이어야 한다는 결론이 나오는 것처럼 보인다. 따라서 우리는 다음 정의에 이르게 된다. ## Definition 세 가지 사건 $E, F, G$가 독립이라고 하는 것은 다음을 만족할 때이다.\begin{aligned} P(E F G) & =P(E) P(F) P(G) \ P(E F) & =P(E) P(F) \ P(E G) & =P(E) P(G) \ P(F G) & =P(F) P(G) \end{aligned}
$E, F, G$가 독립이면 $E$는 $F$와 $G$로 구성된 어떤 사건과도 독립이라는 점에 주목하라. 예를 들어, $E$는 $F \cup G$와 독립이다. 그 이유는 다음과 같다.\begin{aligned} P[E(F \cup G)] & =P(E F \cup E G) \ & =P(E F)+P(E G)-P(E F G) \ & =P(E) P(F)+P(E) P(G)-P(E) P(F G) \ & =P(E)[P(F)+P(G)-P(F G)] \ & =P(E) P(F \cup G) \end{aligned}
물론, 우리는 독립의 정의를 세 개 이상의 사건으로 확장할 수도 있다. 사건 $E_{1}, E_{2}, \ldots, E_{n}$은 이 사건들의 모든 부분집합 $E_{1^{\prime}}, E_{2^{\prime}}, \ldots, E_{r^{\prime}}, r \leq n$에 대해 다음을 만족할 때 독립이라고 한다.P\left(E_{1^{\prime}} E_{2^{\prime}} \cdots E_{r^{\prime}}\right)=P\left(E_{1^{\prime}}\right) P\left(E_{2^{\prime}}\right) \cdots P\left(E_{r^{\prime}}\right)
마지막으로, 무한 개의 사건 집합은 해당 사건들의 모든 유한 부분집합이 독립일 때 독립이라고 정의한다. 때때로 고려 중인 확률 실험은 일련의 **하위 실험(subexperiment)**을 수행하는 것으로 구성된다. 예를 들어, 실험이 동전을 계속 던지는 것으로 구성된다면, 각 던지기를 하위 실험으로 생각할 수 있다. 많은 경우, 하위 실험들의 어떤 그룹의 결과가 다른 하위 실험들의 결과 확률에 영향을 미치지 않는다고 가정하는 것이 합리적이다. 이러한 경우, 우리는 하위 실험들이 **독립적(independent)**이라고 말한다. 더 공식적으로는, $E_{i}$가 $i$번째 하위 실험의 결과에 의해 완전히 결정되는 사건일 때마다 $E_{1}, E_{2}, \ldots, E_{n}, \ldots$이 반드시 독립적인 사건의 시퀀스이면 하위 실험들이 독립적이라고 말한다. 각 하위 실험이 동일한 가능한 결과 집합을 가질 때, 하위 실험들은 종종 **시행(trials)**이라고 불린다. 무한 시퀀스의 독립 시행이 수행될 예정이다. 각 시행은 확률 $p$로 성공하고 확률 $1-p$로 실패한다. 다음 확률은 얼마인가? (a) 처음 $n$번의 시행에서 **최소 1번의 성공**이 발생할 확률; (b) 처음 $n$번의 시행에서 **정확히 $k$번의 성공**이 발생할 확률; (c) **모든 시행이 성공**할 확률? **풀이** 처음 $n$번의 시행에서 최소 1번의 성공이 발생할 확률을 결정하기 위해, 먼저 **여사건(complementary event)**의 확률, 즉 처음 $n$번의 시행에서 성공이 전혀 발생하지 않을 확률을 계산하는 것이 가장 쉽다. $E_{i}$를 $i$번째 시행에서 실패하는 사건이라고 하면, 성공이 전혀 발생하지 않을 확률은 독립성에 의해 다음과 같다.P\left(E_{1} E_{2} \cdots E_{n}\right)=P\left(E_{1}\right) P\left(E_{2}\right) \cdots P\left(E_{n}\right)=(1-p)^{n}
따라서 (a)의 답은 $1-(1-p)^{n}$이다. (b)의 답을 계산하기 위해, 처음 $n$개의 결과 중 $k$번의 성공과 $n-k$번의 실패를 포함하는 특정 시퀀스를 고려해보자. 이러한 시퀀스 각각은 시행의 독립성 가정에 의해 확률 $p^{k}(1-p)^{n-k}$로 발생한다. 이러한 시퀀스는 $\binom{n}{k}$개 있으므로 ($k$번의 성공과 $n-k$번의 실패의 순열은 $n!/ k!(n-k)!$개이다), (b)에서 원하는 확률은 다음과 같다.P{\text { 정확히 } k \text { 번의 성공 }}=\binom{n}{k} p^{k}(1-p)^{n-k}
(c)에 답하기 위해, (a)에 의해 처음 $n$번의 시행이 모두 성공할 확률은 다음과 같이 주어진다는 점에 주목한다.P\left(E_{1}^{c} E_{2}^{c} \cdots E_{n}^{c}\right)=p^{n}
\begin{aligned} P\left(\bigcap_{i=1}^{\infty} E_{i}^{c}\right) & =P\left(\lim {n \rightarrow \infty} \bigcap{i=1}^{n} E_{i}^{c}\right) \ & =\lim {n \rightarrow \infty} P\left(\bigcap{i=1}^{n} E_{i}^{c}\right) \ & =\lim _{n} p^{n}= \begin{cases}0 & \text { if } p<1 \ 1 & \text { if } p=1\end{cases} \end{aligned}
**예제 4g** $n$개의 개별 구성 요소로 구성된 시스템은 **병렬 시스템(parallel system)**이라고 불리는데, 이는 구성 요소 중 적어도 하나가 작동하면 시스템이 작동하기 때문이다. (그림 3.2 참조) 이러한 시스템에서, 다른 구성 요소들과 독립적인 구성 요소 $i$가 확률 $p_{i}, i=1, \ldots, n$로 작동할 때, 시스템이 작동할 확률은 얼마인가? **풀이** $A_{i}$를 구성 요소 $i$가 작동하는 사건이라고 하자. 그러면,\begin{aligned} P{\text { 시스템 작동 }} & =1-P{\text { 시스템 작동 안 함 }} \ & =1-P{\text { 모든 구성 요소가 작동 안 함 }} \ & =1-P\left(\bigcap_{i} A_{i}^{c}\right) \ & =1-\prod_{i=1}^{n}\left(1-p_{i}\right) \quad \text { 독립성에 의해 } \end{aligned}
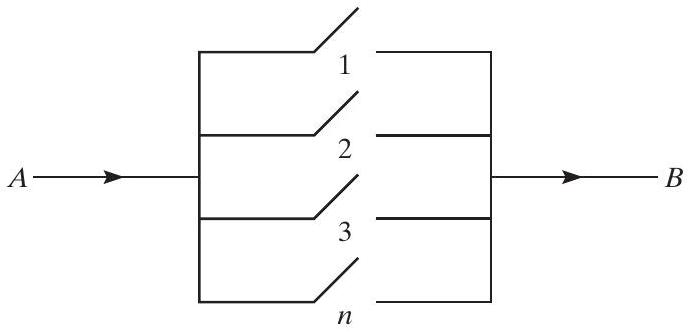 그림 3.2 병렬 시스템: 전류가 $A$에서 $B$로 흐르면 작동한다. ## Example 4h 공정한 주사위 한 쌍을 굴리는 독립적인 시행이 수행된다. 주사위 눈의 합이 결과일 때, 7의 결과가 나타나기 전에 5의 결과가 나타날 확률은 얼마인가? 풀이 $E_n$을 첫 $n-1$번의 시행에서 5 또는 7이 나타나지 않고, $n$번째 시행에서 5가 나타나는 사건이라고 하면, 원하는 확률은 다음과 같다.P\left(\bigcup_{n=1}^{\infty} E_{n}\right)=\sum_{n=1}^{\infty} P\left(E_{n}\right)
이제, $P\{5 \text{ on any trial}\}=\frac{4}{36}$이고 $P\{7 \text{ on any trial}\}=\frac{6}{36}$이므로, 시행의 독립성에 의해 다음을 얻는다.P\left(E_{n}\right)=\left(1-\frac{10}{36}\right)^{n-1} \frac{4}{36}
\begin{aligned} P\left(\bigcup_{n=1}^{\infty} E_{n}\right) & =\frac{1}{9} \sum_{n=1}^{\infty}\left(\frac{13}{18}\right)^{n-1} \ & =\frac{1}{9} \frac{1}{1-\frac{13}{18}} \ & =\frac{2}{5} \end{aligned}
이 결과는 조건부 확률을 사용하여 얻을 수도 있다. $E$를 7이 나타나기 전에 5가 나타나는 사건이라고 하면, 첫 번째 시행의 결과에 따라 조건화함으로써 원하는 확률 $P(E)$를 얻을 수 있다. 다음과 같다: $F$를 첫 번째 시행에서 5가 나오는 사건, $G$를 첫 번째 시행에서 7이 나오는 사건, $H$를 첫 번째 시행에서 5도 7도 아닌 결과가 나오는 사건이라고 하자. 그러면, 이 사건들 중 어느 것이 발생하는지에 따라 조건화하면 다음을 얻는다.P(E)=P(E \mid F) P(F)+P(E \mid G) P(G)+P(E \mid H) P(H)
\begin{aligned} & P(E \mid F)=1 \ & P(E \mid G)=0 \ & P(E \mid H)=P(E) \end{aligned}
처음 두 등식은 명백하다. 세 번째 등식은 첫 번째 결과가 5도 7도 아닌 경우, 그 시점의 상황이 문제가 처음 시작되었을 때와 정확히 같기 때문에 성립한다. 즉, 실험자는 5 또는 7이 나타날 때까지 공정한 주사위 한 쌍을 계속 굴릴 것이다. 또한, 시행은 독립적이므로 첫 번째 시행의 결과는 이후 주사위 굴림에 영향을 미치지 않는다. $P(F)=\frac{4}{36}, P(G)=\frac{6}{36}$, 그리고 $P(H)=\frac{26}{36}$이므로, 다음이 성립한다.P(E)=\frac{1}{9}+P(E) \frac{13}{18}
P(E)=\frac{2}{5}
독자는 이 답이 매우 직관적이라는 점에 주목해야 한다. 즉, 어떤 굴림에서 5가 나타날 확률이 $\frac{4}{36}$이고 7이 나타날 확률이 $\frac{6}{36}$이므로, 7보다 5가 먼저 나타날 확률은 6 대 4의 배당률로 직관적으로 보인다. 그러면 확률은 $\frac{4}{10}$이 되어야 하며, 실제로 그렇다. 동일한 논증은 $E$와 $F$가 어떤 실험의 상호 배타적인 사건일 때, 실험의 독립적인 시행이 수행되면 사건 $E$가 사건 $F$보다 먼저 발생할 확률이 다음과 같음을 보여준다.\frac{P(E)}{P(E)+P(F)}
예제 4i $n$가지 유형의 쿠폰이 있고, 새로 수집되는 각 쿠폰은 이전 선택과 독립적으로 확률 $p_i$로 유형 $i$ 쿠폰이라고 가정하자. 여기서 $\sum_{i=1}^{n} p_{i}=1$이다. $k$개의 쿠폰을 수집한다고 가정하자. $A_i$가 수집된 쿠폰 중에 적어도 하나의 유형 $i$ 쿠폰이 있는 사건일 때, $i \neq j$에 대해 다음을 구하라. (a) $P\left(A_{i}\right)$ (b) $P\left(A_{i} \cup A_{j}\right)$ (c) $P\left(A_{i} \mid A_{j}\right)$ 풀이\begin{aligned} P\left(A_{i}\right) & =1-P\left(A_{i}^{c}\right) \ & =1-P{\text { no coupon is type } i} \ & =1-\left(1-p_{i}\right)^{k} \end{aligned}
위 식은 각 쿠폰이 독립적으로 확률 $1-p_i$로 유형 $i$가 아님을 사용했다. 유사하게,\begin{aligned} P\left(A_{i} \cup A_{j}\right) & =1-P\left(\left(A_{i} \cup A_{j}\right)^{c}\right) \ & =1-P{\text { no coupon is either type } i \text { or type } j} \ & =1-\left(1-p_{i}-p_{j}\right)^{k} \end{aligned}
위 식은 각 쿠폰이 독립적으로 확률 $1-p_i-p_j$로 유형 $i$도 유형 $j$도 아님을 사용했다. $P\left(A_{i} \mid A_{j}\right)$를 구하기 위해 다음 항등식을 사용할 것이다.P\left(A_{i} \cup A_{j}\right)=P\left(A_{i}\right)+P\left(A_{j}\right)-P\left(A_{i} A_{j}\right)
\begin{aligned} P\left(A_{i} A_{j}\right) & =1-\left(1-p_{i}\right)^{k}+1-\left(1-p_{j}\right)^{k}-\left[1-\left(1-p_{i}-p_{j}\right)^{k}\right] \ & =1-\left(1-p_{i}\right)^{k}-\left(1-p_{j}\right)^{k}+\left(1-p_{i}-p_{j}\right)^{k} \end{aligned}
P\left(A_{i} \mid A_{j}\right)=\frac{P\left(A_{i} A_{j}\right)}{P\left(A_{j}\right)}=\frac{1-\left(1-p_{i}\right)^{k}-\left(1-p_{j}\right)^{k}+\left(1-p_{i}-p_{j}\right)^{k}}{1-\left(1-p_{j}\right)^{k}}
다음 예제는 확률론 역사에서 영예로운 위치를 차지하는 문제를 제시한다. 이것은 유명한 **점수 문제(problem of the points)**이다. 일반적인 용어로, 문제는 다음과 같다: 두 플레이어가 판돈을 걸고 어떤 게임을 하는데, 판돈은 게임의 승자에게 돌아간다. 중단으로 인해 어느 쪽도 이기기 전에 멈춰야 하고, 각자 어떤 종류의 "부분 점수"를 가지고 있을 때, 판돈은 어떻게 분배되어야 하는가? 이 문제는 1654년 당시 전문 도박꾼이었던 슈발리에 드 메레(Chevalier de Méré)에 의해 프랑스 수학자 블레즈 파스칼(Blaise Pascal)에게 제기되었다. 이 문제를 다루면서 파스칼은 게임이 그 시점에서 계속된다면 경쟁자들이 받을 상금의 비율이 각자의 승리 확률에 따라 달라져야 한다는 중요한 아이디어를 도입했다. 파스칼은 몇 가지 특수한 경우를 해결했고, 더 중요하게는 위대한 수학자로 명성이 높았던 유명한 프랑스인 피에르 드 페르마(Pierre de Fermat)와 서신 교환을 시작했다. 그 결과로 이루어진 서신 교환은 점수 문제에 대한 완전한 해결책을 제시했을 뿐만 아니라, 우연의 게임과 관련된 다른 많은 문제들의 해결을 위한 틀을 마련했다. 일부에서는 확률론의 탄생일로 여겨지는 이 유명한 서신 교환은 유럽 수학자들 사이에서 확률에 대한 관심을 불러일으키는 데도 중요했다. 왜냐하면 파스칼과 페르마는 당시 최고의 수학자들 중 한 명으로 인정받았기 때문이다. 예를 들어, 그들의 서신 교환 직후 젊은 네덜란드 수학자 크리스티안 하위헌스(Christiaan Huygens)는 이 문제들과 해결책을 논의하기 위해 파리로 왔고, 이 새로운 분야에 대한 관심과 활동은 빠르게 증가했다. ## Example ## The problem of the points 성공 확률이 $p$이고 실패 확률이 $1-p$인 독립적인 시행이 수행된다. $m$번의 실패가 발생하기 전에 $n$번의 성공이 발생할 확률은 얼마인가? 만약 $A$와 $B$가 게임을 하고, 성공 시 $A$가 1점을 얻고 실패 시 $B$가 1점을 얻는다고 생각한다면, 원하는 확률은 $A$가 승리하기 위해 $n$점이 더 필요하고 $B$가 승리하기 위해 $m$점이 더 필요한 상황에서 게임이 계속된다면 $A$가 이길 확률이다. **풀이** 두 가지 풀이를 제시할 것이다. 첫 번째는 **Pascal**의 풀이이고 두 번째는 **Fermat**의 풀이이다. $m$번의 실패가 발생하기 전에 $n$번의 성공이 발생할 확률을 $P_{n, m}$이라고 하자. 첫 번째 시행의 결과에 따라 조건화하면 다음과 같은 식을 얻는다.P_{n, m}=p P_{n-1, m}+(1-p) P_{n, m-1} \quad n \geq 1, m \geq 1
(이유는 무엇인가? 생각해 보라.) 명백한 경계 조건 $P_{n, 0}=0, P_{0, m}=1$을 사용하여 이 방정식들을 $P_{n, m}$에 대해 풀 수 있다. 지루한 세부 사항을 거치기보다는 **Fermat**의 풀이를 살펴보자. **Fermat**는 $m$번의 실패가 발생하기 전에 $n$번의 성공이 발생하기 위해서는 처음 $m+n-1$번의 시행에서 최소한 $n$번의 성공이 있어야 한다고 주장했다. (비록 총 $m+n-1$번의 시행이 완료되기 전에 게임이 끝난다 하더라도, 필요한 추가 시행이 수행되었다고 상상할 수 있다.) 이는 사실이다. 왜냐하면 처음 $m+n-1$번의 시행에서 최소한 $n$번의 성공이 있다면, 그 $m+n-1$번의 시행에서 최대 $m-1$번의 실패가 있을 수 있기 때문에 $m$번의 실패가 발생하기 전에 $n$번의 성공이 발생할 것이다. 그러나 만약 처음 $m+n-1$번의 시행에서 $n$번 미만의 성공이 있었다면, 같은 수의 시행에서 최소한 $m$번의 실패가 있었을 것이므로 $m$번의 실패가 발생하기 전에 $n$번의 성공이 발생하지 않을 것이다. 따라서 예제 4f에서 보았듯이 $m+n-1$번의 시행에서 정확히 $k$번의 성공이 발생할 확률은 $\binom{m+n-1}{k} p^{k}(1-p)^{m+n-1-k}$이므로, $m$번의 실패가 발생하기 전에 $n$번의 성공이 발생할 원하는 확률은 다음과 같다.P_{n, m}=\sum_{k=n}^{m+n-1}\binom{m+n-1}{k} p^{k}(1-p)^{m+n-1-k}
다음 예시는 경기 승자가 결정된 후에도 경기가 계속된다고 가정함으로써 플레이어가 경기에서 이길 확률을 결정하는 것이 더 쉬워지는 또 다른 경우를 보여준다. ## Example 4k ## Service protocol in a serve and rally game 두 선수 $A$와 $B$ 사이의 서브 앤 랠리 경기(예: 배구, 배드민턴, 스쿼시)를 생각해 보자. 경기는 일련의 랠리로 구성되며, 각 랠리는 한 선수의 서브로 시작하여 한 선수가 랠리에서 이길 때까지 계속된다. 랠리에서 이긴 선수는 1점을 얻고, 한 선수가 총 $n$점을 얻으면 경기가 종료되며 그 선수가 경기의 승자로 선언된다. 랠리가 $A$의 서브로 시작할 때, $A$가 랠리에서 이길 확률은 $p_{A}$이고 $B$가 이길 확률은 $q_{A}=1-p_{A}$라고 가정하자. 또한, $B$의 서브로 시작하는 랠리는 $A$가 이길 확률이 $p_{B}$이고 $B$가 이길 확률이 $q_{B}=1-p_{B}$라고 가정하자. 선수 $A$가 첫 서브를 한다. 두 가지 가능한 서브 프로토콜이 고려된다: 1. **"승자 서브(winner serves)"**: 랠리에서 이긴 선수가 다음 랠리의 서브를 한다. 2. **"교대 서브(alternating serve)"**: 서브가 랠리마다 교대되어, 두 랠리 연속으로 같은 선수가 서브하지 않는다. 예를 들어, $n=3$일 때, "승자 서브" 프로토콜에서 연속적인 서브 순서는 $A, B, A, A$가 될 수 있다 (만약 $A$가 첫 포인트를 이기고, $B$가 다음 포인트를 이기고, $A$가 다음 두 포인트를 이긴다면). 반면에 "교대 서브" 프로토콜에서 서브 순서는 경기 승자가 결정될 때까지 항상 $A, B, A, B, A, \ldots$가 된다. 만약 당신이 선수 $A$라면, 어떤 프로토콜을 선호하겠는가? **해답** 놀랍게도, **어떤 프로토콜을 사용하든 $A$가 경기에서 이길 확률은 동일**하므로 차이가 없다. 이를 증명하기 위해, 선수들이 총 $2n-1$개의 랠리가 완료될 때까지 계속 경기를 한다고 가정하는 것이 유리하다. $n$개의 랠리에서 먼저 이긴 선수는 $2n-1$개의 랠리 중 적어도 $n$개를 이긴 선수가 될 것이다. 먼저, **교대 서브 프로토콜**이 사용되는 경우, $2n-1$개의 랠리에서 선수 $A$는 정확히 $n$번 서브하고 선수 $B$는 정확히 $n-1$번 서브한다는 점에 주목하자. 이제 **승자 서브 프로토콜**을 고려하되, 다시 선수들이 $2n-1$개의 랠리가 완료될 때까지 계속 경기를 한다고 가정하자. 경기 승자가 결정된 후의 "추가 랠리"를 누가 서브하는지는 중요하지 않으므로, 경기가 결정된 시점(한 선수가 $n$점을 얻었기 때문에)에 나머지 랠리(있다면)는 모두 경기에서 진 선수가 서브한다고 가정하자. 이 수정된 서브 프로토콜은 경기 승자가 $2n-1$개의 랠리 중 적어도 $n$개를 이긴 선수라는 사실을 변경하지 않는다. 우리는 이 수정된 서브 프로토콜 하에서 $A$는 항상 $n$번 서브하고 $B$는 항상 $n-1$번 서브한다고 주장한다. 두 가지 경우를 통해 이를 보여줄 수 있다. **경우 1: $A$가 경기에서 이긴다.** $A$가 첫 서브를 하기 때문에, $A$의 두 번째 서브는 $A$의 첫 번째 포인트 직후에 이어진다. $A$의 세 번째 서브는 $A$의 두 번째 포인트 직후에 이어진다. 특히, $A$의 $n$번째 서브는 $A$의 $(n-1)$번째 포인트 직후에 이어진다. 그러나 이것이 경기 결과가 결정되기 전 $A$의 마지막 서브가 될 것이다. 왜냐하면 $A$가 그 서브에서 포인트를 이겨 $n$점을 얻거나, $A$가 포인트를 져서 서브가 $B$에게 넘어가고 $A$가 $n$번째 포인트를 얻을 때까지 $B$가 서브를 계속할 것이기 때문이다. 따라서 $A$가 경기에서 이긴다면, 경기가 결정되는 순간 $A$는 총 $n$번 서브했을 것이다. 수정된 서브 프로토콜에 따라 $A$는 다시는 서브하지 않으므로, 이 경우 $A$는 정확히 $n$번 서브한다. **경우 2: $B$가 경기에서 이긴다.** $A$가 첫 서브를 하기 때문에, $B$의 첫 번째 서브는 $B$의 첫 번째 포인트 직후에 이어진다. $B$의 두 번째 서브는 $B$의 두 번째 포인트 직후에 이어진다. 특히, $B$의 $(n-1)$번째 서브는 $B$의 $(n-1)$번째 포인트 직후에 이어진다. 그러나 이것이 경기가 결정되기 전 $B$의 마지막 서브가 될 것이다. 왜냐하면 $B$가 그 서브에서 포인트를 이겨 $n$점을 얻거나, $B$가 포인트를 져서 서브가 $A$에게 넘어가고 $B$가 $n$번째 포인트를 얻을 때까지 $A$가 서브를 계속할 것이기 때문이다. 따라서 $B$가 경기에서 이긴다면, 경기가 결정되는 순간 $B$는 총 $n-1$번 서브했을 것이다. 수정된 서브 프로토콜에 따라 $B$는 다시는 서브하지 않으므로, 이 경우 $B$는 정확히 $n-1$번 서브하고, 총 $2n-1$개의 랠리가 있으므로 $A$는 정확히 $n$번 서브한다. 따라서 우리는 **두 프로토콜 모두에서 $A$는 항상 $n$번 서브하고 $B$는 $n-1$번 서브하며, 경기 승자는 적어도 $n$점을 얻는 선수**라는 것을 알 수 있다. $A$는 자신이 서브하는 각 랠리에서 확률 $p_{A}$로 이기고, $B$가 서브하는 각 랠리에서 확률 $p_{B}$로 이기므로, $A$가 경기 승자가 될 확률은 두 프로토콜 모두에서 동일하다. 이 확률은 $2n-1$개의 독립적인 시도에서 적어도 $n$번 성공할 확률과 같다. 여기서 $n$개의 시도는 확률 $p_{A}$로 성공하고, 나머지 $n-1$개의 시도는 확률 $p_{B}$로 성공한다. 결과적으로, 두 프로토콜의 승리 확률은 동일하다. 다음 두 예시는 도박 문제와 관련이 있으며, 첫 번째 예시는 놀랍도록 우아한 분석을 담고 있다.* **예시 41** 처음에 $r$명의 플레이어가 있고, 플레이어 $i$는 $n_{i}$ 단위를 가지고 있으며, $n_{i}>0, i= 1, \ldots, r$이라고 가정하자. 각 단계에서 두 플레이어가 게임을 하도록 선택되며, 게임의 승자는 패자로부터 1단위를 받는다. 재산이 0으로 떨어지는 플레이어는 제거되며, 한 플레이어가 총 $n \equiv \sum_{i=1}^{r} n_{i}$ 단위를 모두 가질 때까지 계속되며, 그 플레이어가 승자로 지정된다. 연속적인 게임의 결과는 독립적이며 각 게임은 두 플레이어 중 한 명이 이길 확률이 동일하다고 가정할 때, 플레이어 $i$가 승자가 될 확률 $P_{i}$를 구하라. **해답** 먼저, $n$명의 플레이어가 있고 각 플레이어가 처음에 1단위를 가지고 있다고 가정하자. 플레이어 $i$를 고려해 보자. 그녀가 플레이하는 각 단계는 1단위를 이기거나 잃을 확률이 동일하며, 각 단계의 결과는 독립적이다. 또한, 그녀는 재산이 0 또는 $n$이 될 때까지 계속해서 단계를 플레이할 것이다. 이것은 모든 $n$명의 플레이어에게 동일하므로, 각 플레이어는 승자가 될 동일한 기회를 가지며, 이는 각 플레이어가 승자가 될 확률이 $1/n$임을 의미한다. 이제 이 $n$명의 플레이어가 $r$개의 팀으로 나뉘어 있고, 팀 $i$는 $n_{i}$명의 플레이어를 포함한다고 가정하자 ($i=1, \ldots, r$). 그러면 승자가 팀 $i$의 구성원일 확률은 $n_{i}/n$이다. 그러나 다음 사실 때문에: (a) 팀 $i$는 처음에 총 $n_{i}$ 단위를 가지고 있다 ($i=1, \ldots, r$), 그리고 (b) 다른 팀의 구성원들이 플레이하는 각 게임은 두 플레이어 중 한 명이 이길 확률이 동일하며, 승리 팀 구성원의 재산은 1 증가하고 패배 팀 구성원의 재산은 1 감소한다. 승자가 팀 $i$에서 나올 확률이 우리가 원하는 확률과 정확히 같다는 것을 쉽게 알 수 있다. 따라서 $P_{i}=n_{i}/n$이다. 흥미롭게도, 우리의 주장은 이 결과가 각 단계에서 플레이어가 어떻게 선택되는지에 의존하지 않는다는 것을 보여준다. 도박사의 파산 문제에서는 도박사가 2명뿐이지만, 그들이 동등한 실력을 가지고 있다고 가정하지는 않는다. ## Example 4m ## The gambler's ruin problem 두 명의 도박꾼 $A$와 $B$는 연속적인 동전 던지기 결과에 돈을 건다. 매번 동전이 앞면이 나오면 $A$는 $B$로부터 1단위를 얻고, 뒷면이 나오면 $A$는 $B$에게 1단위를 지불한다. 둘 중 한 명이 돈을 모두 잃을 때까지 이 과정을 계속한다. 연속적인 동전 던지기가 독립적이며 각 던지기에서 앞면이 나올 확률이 $p$라고 가정할 때, $A$가 $i$단위로 시작하고 $B$가 $N-i$단위로 시작할 경우 $A$가 모든 돈을 갖게 될 확률은 얼마인가? **풀이** $A$가 $i$단위로 시작하고 $B$가 $N-i$단위로 시작할 때 $A$가 모든 돈을 갖게 되는 사건을 $E$라고 하자. $A$의 초기 자산에 대한 의존성을 명확히 하기 위해 $P_{i}=P(E)$라고 하자. 첫 번째 동전 던지기의 결과에 따라 조건부 확률을 사용하여 $P(E)$에 대한 표현을 얻을 것이다. 첫 번째 던지기에서 앞면이 나오는 사건을 $H$라고 하면,\begin{aligned} P_{i}=P(E) & =P(E \mid H) P(H)+P\left(E \mid H^{c}\right) P\left(H^{c}\right) \ & =p P(E \mid H)+(1-p) P\left(E \mid H^{c}\right) \end{aligned}
이제 첫 번째 던지기에서 앞면이 나왔다고 가정하면, 첫 번째 베팅 후 상황은 $A$가 $i+1$단위를 가지고 $B$가 $N-(i+1)$단위를 갖게 된다. 연속적인 던지기가 독립적이며 앞면이 나올 공통 확률이 $p$라고 가정했으므로, 그 시점부터 $A$가 모든 돈을 얻을 확률은 마치 게임이 $A$가 $i+1$의 초기 자산을 가지고 $B$가 $N-(i+1)$의 초기 자산을 가지고 막 시작하는 것과 정확히 동일하다. 따라서,P(E \mid H)=P_{i+1}
P\left(E \mid H^{c}\right)=P_{i-1}
그러므로 $q=1-p$라고 하면, 다음을 얻는다.P_{i}=p P_{i+1}+q P_{i-1} \quad i=1,2, \ldots, N-1
명백한 경계 조건 $P_{0}=0$과 $P_{N}=1$을 사용하여 이제 방정식 (4.2)를 풀 것이다. $p+q=1$이므로, 이 방정식들은 다음과 동등하다.p P_{i}+q P_{i}=p P_{i+1}+q P_{i-1}
P_{i+1}-P_{i}=\frac{q}{p}\left(P_{i}-P_{i-1}\right) \quad i=1,2, \ldots, N-1
따라서 $P_{0}=0$이므로, 방정식 (4.3)으로부터 다음을 얻는다.\begin{aligned} P_{2}-P_{1} & =\frac{q}{p}\left(P_{1}-P_{0}\right)=\frac{q}{p} P_{1} \ P_{3}-P_{2} & =\frac{q}{p}\left(P_{2}-P_{1}\right)=\left(\frac{q}{p}\right)^{2} P_{1} \ & \cdot \ & \cdot \ P_{i}-P_{i-1} & =\frac{q}{p}\left(P_{i-1}-P_{i-2}\right)=\left(\frac{q}{p}\right)^{i-1} P_{1} \ & \cdot \ & \cdot \ P_{N}-P_{N-1} & =\frac{q}{p}\left(P_{N-1}-P_{N-2}\right)=\left(\frac{q}{p}\right)^{N-1} P_{1} \end{aligned}
(4.4)의 처음 $i-1$개 방정식을 더하면 다음을 얻는다.P_{i}-P_{1}=P_{1}\left[\left(\frac{q}{p}\right)+\left(\frac{q}{p}\right)^{2}+\cdots+\left(\frac{q}{p}\right)^{i-1}\right]
P_{i}=\left{\begin{array}{lc} \frac{1-(q / p)^{i}}{1-(q / p)} P_{1} & \text { if } \frac{q}{p} \neq 1 \ i P_{1} & \text { if } \frac{q}{p}=1 \end{array}\right.
$P_{N}=1$이라는 사실을 사용하면 다음을 얻는다.P_{1}= \begin{cases}\frac{1-(q / p)}{1-(q / p)^{N}} & \text { if } p \neq \frac{1}{2} \ \frac{1}{N} & \text { if } p=\frac{1}{2}\end{cases}
P_{i}= \begin{cases}\frac{1-(q / p)^{i}}{1-(q / p)^{N}} & \text { if } p \neq \frac{1}{2} \ \frac{i}{N} & \text { if } p=\frac{1}{2}\end{cases}
$A$가 $i$단위로 시작하고 $B$가 $N-i$단위로 시작할 때 $B$가 모든 돈을 갖게 될 확률을 $Q_{i}$라고 하자. 그러면 설명된 상황에 대한 대칭성에 따라, $p$를 $q$로, $i$를 $N-i$로 대체하면 다음을 얻는다.Q_{i}= \begin{cases}\frac{1-(p / q)^{N-i}}{1-(p / q)^{N}} & \text { if } q \neq \frac{1}{2} \ \frac{N-i}{N} & \text { if } q=\frac{1}{2}\end{cases}
또한, $q=\frac{1}{2}$는 $p=\frac{1}{2}$와 동등하므로, $q \neq \frac{1}{2}$일 때 다음을 얻는다.\begin{aligned} P_{i}+Q_{i} & =\frac{1-(q / p)^{i}}{1-(q / p)^{N}}+\frac{1-(p / q)^{N-i}}{1-(p / q)^{N}} \ & =\frac{p^{N}-p^{N}(q / p)^{i}}{p^{N}-q^{N}}+\frac{q^{N}-q^{N}(p / q)^{N-i}}{q^{N}-p^{N}} \ & =\frac{p^{N}-p^{N-i} q^{i}-q^{N}+q^{i} p^{N-i}}{p^{N}-q^{N}} \ & =1 \end{aligned}
이 결과는 $p=q=\frac{1}{2}$일 때도 성립하므로,P_{i}+Q_{i}=1
다시 말해, 이 방정식은 확률 1로 $A$ 또는 $B$ 중 한 명이 모든 돈을 갖게 될 것이라는 것을 의미한다. 즉, $A$의 자산이 항상 1과 $N-1$ 사이에 머물면서 게임이 무한정 계속될 확률은 0이다. (독자는 주의해야 한다. 이 도박 게임의 가능한 결과는 선험적으로 두 가지가 아니라 세 가지이다: $A$가 이기거나, $B$가 이기거나, 아무도 이기지 못하고 게임이 영원히 계속되거나. 우리는 방금 마지막 사건의 확률이 0임을 보였다.) 앞선 결과에 대한 수치적 예시로, 만약 $A$가 5단위로 시작하고 $B$가 10단위로 시작한다면, $p$가 $\frac{1}{2}$일 때 $A$가 이길 확률은 $\frac{1}{3}$이 될 것이다. 반면 $p$가 .6이라면 확률은\frac{1-\left(\frac{2}{3}\right)^{5}}{1-\left(\frac{2}{3}\right)^{15}} \approx .87
로 급증할 것이다. **도박꾼의 파산 문제(gambler's ruin problem)**의 특별한 경우로, **지속 시간 문제(problem of duration of play)**라고도 알려진 이 문제는 1657년 페르마가 호이겐스에게 제안했다. 호이겐스 자신이 해결한 버전은 $A$와 $B$가 각각 12개의 동전을 가지고 있다는 것이었다. 그들은 3개의 주사위를 사용하는 게임에서 이 동전들을 걸고 플레이한다: 11이 나올 때마다 (누가 주사위를 굴리든 상관없다) $A$는 $B$에게 동전 하나를 준다. 14가 나올 때마다 $B$는 $A$에게 동전 하나를 준다. 모든 동전을 먼저 얻는 사람이 게임에서 이긴다. $P\{\text{roll 11}\}=\frac{27}{216}$이고 $P\{\text{roll 14}\}=\frac{15}{216}$이므로, 예시 4h에서 보듯이, $A$에게 이것은 $p=\frac{15}{42}$, $i=12$, $N=24$인 도박꾼의 파산 문제와 같다. 도박꾼의 파산 문제의 일반적인 형태는 수학자 제임스 베르누이에 의해 해결되었고, 그의 사망 8년 후인 1713년에 출판되었다. 도박꾼의 파산 문제를 약물 테스트에 적용하는 예시를 살펴보자. 특정 질병 치료를 위해 두 가지 신약이 개발되었다고 가정하자. 약물 $i$는 치료율 $P_{i}, i=1,2$를 가지는데, 이는 약물 $i$로 치료받은 각 환자가 확률 $P_{i}$로 완치될 것임을 의미한다. 그러나 이 치료율은 알려져 있지 않으며, 우리는 $P_{1}>P_{2}$인지 $P_{2}>P_{1}$인지 결정하는 방법을 찾는 데 관심이 있다. 이 대안 중 하나를 결정하기 위해 다음 테스트를 고려한다: 환자 쌍을 순차적으로 치료하며, 한 쌍의 한 구성원은 약물 1을, 다른 구성원은 약물 2를 투여받는다. 각 쌍의 결과가 결정되고, 한 약물로부터의 누적 치료 횟수가 다른 약물로부터의 누적 치료 횟수를 미리 정해진 고정된 수만큼 초과할 때 테스트가 중단된다. 더 공식적으로,\begin{aligned} & X_{j}= \begin{cases}1 & \text { if the patient in the } j \text { th pair that receives drug } 1 \text { is cured } \ 0 & \text { otherwise }\end{cases} \ & Y_{j}= \begin{cases}1 & \text { if the patient in the } j \text { th pair that receives drug } 2 \text { is cured } \ 0 & \text { otherwise }\end{cases} \end{aligned}
미리 정해진 양의 정수 $M$에 대해, 테스트는 $N$번째 쌍 이후에 중단된다. 여기서 $N$은 다음 중 하나를 만족하는 첫 번째 $n$ 값이다.X_{1}+\cdots+X_{n}-\left(Y_{1}+\cdots+Y_{n}\right)=M
X_{1}+\cdots+X_{n}-\left(Y_{1}+\cdots+Y_{n}\right)=-M
전자의 경우, 우리는 $P_{1}>P_{2}$라고 주장하고 후자의 경우 $P_{2}>P_{1}$이라고 주장한다. 앞서 언급한 것이 좋은 테스트인지 확인하는 데 도움이 되기 위해, 우리가 알고 싶은 한 가지는 잘못된 결정을 내릴 확률이다. 즉, 주어진 $P_{1}$과 $P_{2}$에 대해, $P_{1}>P_{2}$일 때, 테스트가 $P_{2}>P_{1}$이라고 잘못 주장할 확률은 얼마인가? 이 확률을 결정하기 위해, 각 쌍이 확인된 후, 약물 1 대 약물 2를 사용한 치료의 누적 차이가 확률 $P_{1}\left(1-P_{2}\right)$로 1 증가하거나 (약물 1이 치료로 이어지고 약물 2는 그렇지 않을 확률이므로), 확률 $\left(1-P_{1}\right) P_{2}$로 1 감소하거나, 확률 $P_{1} P_{2}+\left(1-P_{1}\right)\left(1-P_{2}\right)$로 동일하게 유지된다는 점에 주목하자. 따라서, 누적 차이가 변하는 쌍만 고려한다면, 차이는 확률 $P$로 1 증가할 것이다.\begin{aligned} P & =P{\text { up 1|up 1 or down 1 }} \ & =\frac{P_{1}\left(1-P_{2}\right)}{P_{1}\left(1-P_{2}\right)+\left(1-P_{1}\right) P_{2}} \end{aligned}
그리고 확률 $1-P$로 1 감소할 것이다.1-P=\frac{P_{2}\left(1-P_{1}\right)}{P_{1}\left(1-P_{2}\right)+\left(1-P_{1}\right) P_{2}}
따라서, 테스트가 $P_{2}>P_{1}$이라고 주장할 확률은 각 (1단위) 베팅에서 확률 $P$로 이기는 도박꾼이 $M$만큼 올라가기 전에 $M$만큼 내려갈 확률과 같다. 그러나 방정식 (4.5)에서 $i=M, N=2M$을 사용하면 이 확률은 다음과 같이 주어진다.\begin{aligned} & P\left{\text { test asserts that } P_{2}>P_{1}\right} \ & \quad=1-\frac{1-\left(\frac{1-P}{P}\right)^{M}}{1-\left(\frac{1-P}{P}\right)^{2 M}} \ & \quad=1-\frac{1}{1+\left(\frac{1-P}{P}\right)^{M}} \ & \quad=\frac{1}{1+\gamma^{M}} \end{aligned}
\gamma=\frac{P}{1-P}=\frac{P_{1}\left(1-P_{2}\right)}{P_{2}\left(1-P_{1}\right)}
예를 들어, $P_{1}=.6$이고 $P_{2}=.4$일 때, $M=5$이면 잘못된 결정의 확률은 .017이고, $M=10$이면 .0003으로 감소한다. 어떤 요소들의 집합이 주어졌을 때, 그 집합의 적어도 한 구성원이 특정 속성을 가지고 있는지 여부를 결정하고 싶다고 가정하자. 우리는 각 요소가 선택될 양의 확률을 갖도록 집합의 요소를 무작위로 선택함으로써 이 질문에 확률적으로 접근할 수 있다. 그러면 원래의 질문은 무작위로 선택된 요소가 관심 속성을 가지고 있지 않을 확률을 고려함으로써 답할 수 있다. 이 확률이 1과 같으면 집합의 어떤 요소도 그 속성을 가지고 있지 않다. 1보다 작으면 집합의 적어도 한 요소가 그 속성을 가지고 있다. 이 섹션의 마지막 예시는 이 기법을 보여준다. ## Example $n$개의 꼭짓점을 갖는 완전 그래프는 평면상의 $n$개의 점(꼭짓점이라 함)과 각 꼭짓점 쌍을 연결하는 $\binom{n}{2}$개의 선(모서리라 함)의 집합으로 정의된다. 3개의 꼭짓점을 갖는 완전 그래프는 Figure 3.3에 나와 있다. 이제 $n$개의 꼭짓점을 갖는 완전 그래프의 각 모서리를 빨간색 또는 파란색으로 칠한다고 가정해 보자. 고정된 정수 $k$에 대해 흥미로운 질문은, $k$개의 꼭짓점 집합 중 어느 것도 $\binom{k}{2}$개의 연결 모서리가 모두 같은 색이 되지 않도록 모서리를 칠하는 방법이 있는가? 이 질문에 대한 답은 $n$이 너무 크지 않으면 '예'라는 것을 확률론적 논증으로 보일 수 있다. 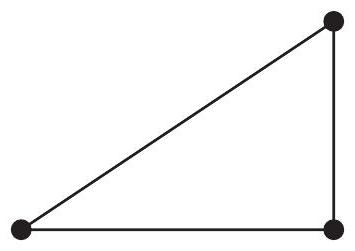 Figure 3.3 논증은 다음과 같다: 각 모서리가 독립적으로 빨간색 또는 파란색으로 칠해질 확률이 같다고 가정한다. 즉, 각 모서리가 $\frac{1}{2}$의 확률로 빨간색이라고 가정한다. $k$개의 꼭짓점 집합 $\binom{n}{k}$개에 번호를 매기고, 사건 $E_{i}, i=1, \ldots,\binom{n}{k}$를 다음과 같이 정의한다:\begin{aligned} E_{i}= & {\text { } i \text {번째 } k \text {개 꼭짓점 집합의 모든 연결 모서리가 같은 색인 경우 } } \end{aligned}
이제 $k$개의 꼭짓점 집합의 $\binom{k}{2}$개 연결 모서리 각각이 빨간색 또는 파란색일 확률이 같으므로, 이들이 모두 같은 색일 확률은 다음과 같다:P\left(E_{i}\right)=2\left(\frac{1}{2}\right)^{k(k-1) / 2}
P\left(\bigcup_{i} E_{i}\right) \leq \sum_{i} P\left(E_{i}\right) \quad \text { (Boole's inequality) }
이므로, 모든 연결 모서리가 같은 색인 $k$개의 꼭짓점 집합이 존재할 확률인 $P\left(\bigcup_{i} E_{i}\right)$는 다음을 만족한다:P\left(\bigcup_{i} E_{i}\right) \leq\binom{ n}{k}\left(\frac{1}{2}\right)^{k(k-1) / 2-1}
\binom{n}{k}\left(\frac{1}{2}\right)^{k(k-1) / 2-1}<1
\binom{n}{k}<2^{k(k-1) / 2-1}
이라면, $\binom{n}{k}$개의 $k$개 꼭짓점 집합 중 적어도 하나가 모든 연결 모서리가 같은 색일 확률은 1보다 작다. 결과적으로, $n$과 $k$에 대한 앞선 조건 하에서, 어떤 $k$개 꼭짓점 집합도 모든 연결 모서리가 같은 색이 아닐 양의 확률이 존재한다. 그러나 이 결론은 어떤 $k$개 꼭짓점 집합도 모든 연결 모서리가 같은 색이 아닌 방식으로 모서리를 칠하는 방법이 적어도 하나 존재한다는 것을 의미한다. 비고 (a) 앞선 논증은 원하는 속성을 만족하는 색칠 방식의 존재를 보장하는 $n$과 $k$에 대한 조건을 확립했지만, 그러한 방식을 얻는 방법에 대한 정보는 제공하지 않는다 (비록 한 가지 가능성은 단순히 색을 무작위로 선택하고, 결과 색칠이 속성을 만족하는지 확인하고, 만족할 때까지 절차를 반복하는 것일 수 있다). (b) 순전히 결정론적인 문제에 확률을 도입하는 방법을 **확률론적 방법(probabilistic method)**이라고 부른다. 이 방법의 다른 예시는 Theoretical Exercise 24와 Chapter 7의 Examples 2t 및 2u에 나와 있다. ## 3.5 $\mathbf{P}(\cdot \mid \boldsymbol{F})$ Is a Probability 조건부 확률은 일반 확률의 모든 속성을 만족하며, 이는 $P(E \mid F)$가 확률의 세 가지 공리를 만족함을 보여주는 명제 5.1에 의해 증명된다. 명제 5.1 (a) $0 \leq P(E \mid F) \leq 1$. (b) $P(S \mid F)=1$. (c) $E_{i}, i=1,2, \ldots$가 상호 배타적인 사건일 때, 다음이 성립한다.P\left(\bigcup_{i=1}^{\infty} E_{i} \mid F\right)=\sum_{i=1}^{\infty} P\left(E_{i} \mid F\right)
증명 (a)를 증명하기 위해 $0 \leq P(E F) / P(F) \leq 1$임을 보여야 한다. 왼쪽 부등식은 자명하며, 오른쪽 부등식은 $E F \subset F$이므로 $P(E F) \leq P(F)$가 성립하기 때문에 따른다. (b)는 다음으로부터 따른다.P(S \mid F)=\frac{P(S F)}{P(F)}=\frac{P(F)}{P(F)}=1
\begin{aligned} P\left(\bigcup_{i=1}^{\infty} E_{i} \mid F\right) & =\frac{P\left(\left(\bigcup_{i=1}^{\infty} E_{i}\right) F\right)}{P(F)} \ & =\frac{P\left(\bigcup_{1}^{\infty} E_{i} F\right)}{P(F)} \text { since }\left(\bigcup_{1}^{\infty} E_{i}\right) F=\bigcup_{1}^{\infty} E_{i} F \ & =\frac{\sum_{1}^{\infty} P\left(E_{i} F\right)}{P(F)} \ & =\sum_{1}^{\infty} P\left(E_{i} \mid F\right) \end{aligned}
여기서 마지막에서 두 번째 등식은 $E_{i} E_{j}=\varnothing$이 $E_{i} F E_{j} F=\varnothing$을 의미하기 때문에 성립한다. 만약 $Q(E)=P(E \mid F)$로 정의한다면, 명제 5.1에 따라 $Q(E)$는 $S$의 사건들에 대한 확률 함수로 간주될 수 있다. 따라서 이전에 확률에 대해 증명된 모든 명제는 $Q(E)$에도 적용된다. 예를 들어, 다음이 성립한다.Q\left(E_{1} \cup E_{2}\right)=Q\left(E_{1}\right)+Q\left(E_{2}\right)-Q\left(E_{1} E_{2}\right)
P\left(E_{1} \cup E_{2} \mid F\right)=P\left(E_{1} \mid F\right)+P\left(E_{2} \mid F\right)-P\left(E_{1} E_{2} \mid F\right)
또한, 조건부 확률 $Q\left(E_{1} \mid E_{2}\right)$를 $Q\left(E_{1} \mid E_{2}\right)=Q\left(E_{1} E_{2}\right) / Q\left(E_{2}\right)$로 정의하면, 식 (3.1)로부터 다음을 얻는다.Q\left(E_{1}\right)=Q\left(E_{1} \mid E_{2}\right) Q\left(E_{2}\right)+Q\left(E_{1} \mid E_{2}^{c}\right) Q\left(E_{2}^{c}\right)
\begin{aligned} Q\left(E_{1} \mid E_{2}\right) & =\frac{Q\left(E_{1} E_{2}\right)}{Q\left(E_{2}\right)} \ & =\frac{P\left(E_{1} E_{2} \mid F\right)}{P\left(E_{2} \mid F\right)} \ & =\frac{\frac{P\left(E_{1} E_{2} F\right)}{P(F)}}{\frac{P\left(E_{2} F\right)}{P(F)}} \ & =P\left(E_{1} \mid E_{2} F\right) \end{aligned}
P\left(E_{1} \mid F\right)=P\left(E_{1} \mid E_{2} F\right) P\left(E_{2} \mid F\right)+P\left(E_{1} \mid E_{2}^{c} F\right) P\left(E_{2}^{c} \mid F\right)
사고를 겪을 확률은 .4인 반면, 사고를 겪지 않는 사람의 해당 수치는 .2이다. 새 보험 가입자가 첫 해에 사고를 겪었다고 가정할 때, 두 번째 해에 사고를 겪을 조건부 확률은 얼마인가? 해결책 보험 가입자가 사고를 잘 겪는 사람일 사건을 $A$라고 하고, $i$번째 해에 사고를 겪을 사건을 $A_{i}, i=1,2$라고 하자. 그러면 원하는 확률 $P\left(A_{2} \mid A_{1}\right)$은 보험 가입자가 사고를 잘 겪는 사람인지 아닌지에 따라 다음과 같이 조건화하여 얻을 수 있다.P\left(A_{2} \mid A_{1}\right)=P\left(A_{2} \mid A A_{1}\right) P\left(A \mid A_{1}\right)+P\left(A_{2} \mid A^{c} A_{1}\right) P\left(A^{c} \mid A_{1}\right)
P\left(A \mid A_{1}\right)=\frac{P\left(A_{1} A\right)}{P\left(A_{1}\right)}=\frac{P\left(A_{1} \mid A\right) P(A)}{P\left(A_{1}\right)}
그러나 $P(A)$는 $\frac{3}{10}$과 같다고 가정하며, 예제 3a에서 $P\left(A_{1}\right)=$ .26임이 밝혀졌다. 따라서,P\left(A \mid A_{1}\right)=\frac{(.4)(.3)}{.26}=\frac{6}{13}
P\left(A^{c} \mid A_{1}\right)=1-P\left(A \mid A_{1}\right)=\frac{7}{13}
$P\left(A_{2} \mid A A_{1}\right)=.4$이고 $P\left(A_{2} \mid A^{c} A_{1}\right)=.2$이므로, 다음이 성립한다.P\left(A_{2} \mid A_{1}\right)=(.4) \frac{6}{13}+(.2) \frac{7}{13} \approx .29
예제 5b 암컷 침팬지가 새끼를 낳았다. 그러나 두 수컷 침팬지 중 누가 아빠인지는 확실하지 않다. 유전자 분석이 수행되기 전에는 수컷 1이 아빠일 확률이 $p$이고 수컷 2가 아빠일 확률이 $1-p$라고 믿어진다. 어미, 수컷 1, 수컷 2로부터 얻은 DNA는 게놈의 한 특정 위치에서 어미는 유전자 쌍 $(A, A)$를 가지고 있고, 수컷 1은 유전자 쌍 $(a, a)$를 가지고 있으며, 수컷 2는 유전자 쌍 $(A, a)$를 가지고 있음을 나타낸다. DNA 검사 결과 아기 침팬지가 유전자 쌍 $(A, a)$를 가지고 있다면, 수컷 1이 아빠일 확률은 얼마인가? 해결책 모든 확률은 어미가 유전자 쌍 $(A, A)$를 가지고 있고, 수컷 1이 유전자 쌍 $(a, a)$를 가지고 있으며, 수컷 2가 유전자 쌍 $(A, a)$를 가지고 있다는 사건에 조건부로 한다. 이제 수컷 $i, i=1,2$가 아빠일 사건을 $M_{i}$라고 하고, 아기 침팬지가 유전자 쌍 $(A, a)$를 가질 사건을 $B_{A, a}$라고 하자. 그러면 $P\left(M_{1} \mid B_{A, a}\right)$는 다음과 같이 얻어진다.\begin{aligned} P\left(M_{1} \mid B_{A, a}\right) & =\frac{P\left(M_{1} B_{A, a}\right)}{P\left(B_{A, a}\right)} \ & =\frac{P\left(B_{A, a} \mid M_{1}\right) P\left(M_{1}\right)}{P\left(B_{A, a} \mid M_{1}\right) P\left(M_{1}\right)+P\left(B_{A, a} \mid M_{2}\right) P\left(M_{2}\right)} \ & =\frac{1 \cdot p}{1 \cdot p+(1 / 2)(1-p)} \ & =\frac{2 p}{1+p} \end{aligned}
$p<1$일 때 $\frac{2 p}{1+p}>p$이므로, 아기의 유전자 쌍이 $(A, a)$라는 정보는 수컷 1이 아빠일 확률을 증가시킨다. 이 결과는 직관적이다. 왜냐하면 $M_{1}$이 사실일 때 아기가 유전자 쌍 $(A, a)$를 가질 가능성이 $M_{2}$가 사실일 때보다 더 높기 때문이다 (각각의 조건부 확률은 1과 $1/2$). $\square$ 다음 예제는 런(runs) 이론의 문제와 관련이 있다. ## Example 5c 각각 성공 확률이 $p$이고 실패 확률이 $q=1-p$인 독립적인 시행이 수행된다. 우리는 **$m$번 연속 실패가 발생하기 전에 $n$번 연속 성공이 발생할 확률**을 계산하는 데 관심이 있다. 해결책 $E$를 $m$번 연속 실패가 발생하기 전에 $n$번 연속 성공이 발생하는 사건이라고 하자. $P(E)$를 구하기 위해 첫 번째 시행의 결과에 따라 조건부 확률을 적용한다. 즉, $H$를 첫 번째 시행이 성공하는 사건이라고 하면, 다음을 얻는다.P(E)=p P(E \mid H)+q P\left(E \mid H^{c}\right)
이제 첫 번째 시행이 성공했다고 가정할 때, $m$번 연속 실패가 발생하기 전에 $n$번 연속 성공을 얻는 한 가지 방법은 다음 $n-1$번의 시행이 모두 성공하는 것이다. 따라서, 이 사건이 발생하는지 여부에 따라 조건부 확률을 적용하자. 즉, $F$를 2번째부터 $n$번째 시행까지 모두 성공하는 사건이라고 하면, 다음을 얻는다.P(E \mid H)=P(E \mid F H) P(F \mid H)+P\left(E \mid F^{c} H\right) P\left(F^{c} \mid H\right)
한편, 분명히 $P(E \mid F H)=1$이다. 다른 한편으로, 만약 사건 $F^{c} H$가 발생하면, 첫 번째 시행은 성공하지만 다음 $n-1$번의 시행 중 어느 시점에서 실패가 발생할 것이다. 그러나 이 실패가 발생하면 이전의 모든 성공은 무효화되고, 상황은 마치 실패로 시작한 것과 정확히 같아진다. 따라서,P\left(E \mid F^{c} H\right)=P\left(E \mid H^{c}\right)
시행의 독립성은 $F$와 $H$가 독립임을 의미하고, $P(F)=p^{n-1}$이므로, 식 (5.3)으로부터 다음이 도출된다.P(E \mid H)=p^{n-1}+\left(1-p^{n-1}\right) P\left(E \mid H^{c}\right)
이제 유사한 방식으로 $P\left(E \mid H^{c}\right)$에 대한 표현을 얻는다. 즉, $G$를 2번째부터 $m$번째 시행까지 모두 실패하는 사건이라고 하자. 그러면,P\left(E \mid H^{c}\right)=P\left(E \mid G H^{c}\right) P\left(G \mid H^{c}\right)+P\left(E \mid G^{c} H^{c}\right) P\left(G^{c} \mid H^{c}\right)
이제 $G H^{c}$는 처음 $m$번의 시행이 모두 실패하는 사건이므로, $P\left(E \mid G H^{c}\right)=0$이다. 또한, 만약 $G^{c} H^{c}$가 발생하면, 첫 번째 시행은 실패하지만 다음 $m-1$번의 시행 중 적어도 하나의 성공이 있다. 따라서, 이 성공은 이전의 모든 실패를 무효화하므로, 다음을 알 수 있다.P\left(E \mid G^{c} H^{c}\right)=P(E \mid H)
그러므로, $P\left(G^{c} \mid H^{c}\right)=P\left(G^{c}\right)=1-q^{m-1}$이므로, (5.5)로부터 다음을 얻는다.P\left(E \mid H^{c}\right)=\left(1-q^{m-1}\right) P(E \mid H)
P(E \mid H)=\frac{p^{n-1}}{p^{n-1}+q^{m-1}-p^{n-1} q^{m-1}}
P\left(E \mid H^{c}\right)=\frac{\left(1-q^{m-1}\right) p^{n-1}}{p^{n-1}+q^{m-1}-p^{n-1} q^{m-1}}
\begin{aligned} P(E) & =p P(E \mid H)+q P\left(E \mid H^{c}\right) \ & =\frac{p^{n}+q p^{n-1}\left(1-q^{m-1}\right)}{p^{n-1}+q^{m-1}-p^{n-1} q^{m-1}} \ & =\frac{p^{n-1}\left(1-q^{m}\right)}{p^{n-1}+q^{m-1}-p^{n-1} q^{m-1}} \end{aligned}
문제의 대칭성에 의해, **$n$번 연속 성공이 발생하기 전에 $m$번 연속 실패가 발생할 확률**은 $p$와 $q$를 서로 바꾸고 $n$과 $m$을 서로 바꾼 식 (5.7)로 주어진다는 점은 흥미롭다. 따라서, 이 확률은 다음과 같다.\begin{aligned} & P{\text { run of } m \text { failures before a run of } n \text { successes } } \ & =\frac{q^{m-1}\left(1-p^{n}\right)}{q^{m-1}+p^{n-1}-q^{m-1} p^{n-1}} \end{aligned}
식 (5.7)과 (5.8)의 합이 1이므로, 확률 1로 $n$번 연속 성공 또는 $m$번 연속 실패 중 하나가 결국 발생할 것이다. 식 (5.7)의 예시로, 공정한 동전을 던질 때 3번 연속 뒷면이 나오기 전에 2번 연속 앞면이 나올 확률은 $\frac{7}{10}$이다. 4번 연속 뒷면이 나오기 전에 2번 연속 앞면이 나올 확률은 $\frac{5}{6}$으로 증가한다. $\square$ 다음 예시에서는 매칭 문제로 돌아가 조건부 확률을 사용하여 해를 구한다. ## Example 5d 파티에서 $n$명의 남자가 모자를 벗는다. 모자는 섞이고, 각 남자는 무작위로 하나를 선택한다. 남자가 자신의 모자를 선택하면 **일치(match)**가 발생했다고 말한다. 다음 확률은 얼마인가? (a) 일치가 없는 경우 (b) 정확히 $k$개의 일치가 있는 경우 $\square$ 해답 (a) 일치가 발생하지 않는 사건을 $E$라고 하고, $n$에 대한 의존성을 명시하기 위해 $P_{n}=P(E)$라고 쓴다. 첫 번째 남자가 자신의 모자를 선택하는지 여부에 따라 조건부 확률을 계산한다. 이 사건들을 각각 $M$과 $M^{c}$라고 부르면,P_{n}=P(E)=P(E \mid M) P(M)+P\left(E \mid M^{c}\right) P\left(M^{c}\right)
명백히 $P(E \mid M)=0$이므로,P_{n}=P\left(E \mid M^{c}\right) \frac{n-1}{n}
이제 $P\left(E \mid M^{c}\right)$는 $n-1$명의 남자가 이들 중 한 남자의 모자를 포함하지 않는 $n-1$개의 모자 세트에서 선택할 때 일치가 없는 확률이다. 이는 두 가지 상호 배타적인 방식으로 발생할 수 있다: 일치가 없고 추가 남자가 추가 모자(처음 선택한 남자의 모자)를 선택하지 않는 경우, 또는 일치가 없고 추가 남자가 추가 모자를 선택하는 경우. 첫 번째 사건의 확률은 단순히 $P_{n-1}$이며, 이는 추가 모자를 추가 남자의 "소유"로 간주함으로써 알 수 있다. 두 번째 사건의 확률은 $[1 /(n-1)] P_{n-2}$이므로,P\left(E \mid M^{c}\right)=P_{n-1}+\frac{1}{n-1} P_{n-2}
P_{n}=\frac{n-1}{n} P_{n-1}+\frac{1}{n} P_{n-2}
P_{n}-P_{n-1}=-\frac{1}{n}\left(P_{n-1}-P_{n-2}\right)
그러나 $P_{n}$은 $n$명의 남자가 자신의 모자 중에서 선택할 때 일치가 없는 확률이므로,P_{1}=0 \quad P_{2}=\frac{1}{2}
\begin{aligned} & P_{3}-P_{2}=-\frac{\left(P_{2}-P_{1}\right)}{3}=-\frac{1}{3!} \quad \text { 또는 } \quad P_{3}=\frac{1}{2!}-\frac{1}{3!} \ & P_{4}-P_{3}=-\frac{\left(P_{3}-P_{2}\right)}{4}=\frac{1}{4!} \quad \text { 또는 } \quad P_{4}=\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!} \end{aligned}
P_{n}=\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-\cdots+\frac{(-1)^{n}}{n!}
(b) 정확히 $k$개의 일치가 발생할 확률을 구하기 위해, 임의의 고정된 $k$명의 그룹을 고려한다. 이들만이 자신의 모자를 선택할 확률은 다음과 같다:\frac{1}{n} \frac{1}{n-1} \cdots \frac{1}{n-(k-1)} P_{n-k}=\frac{(n-k)!}{n!} P_{n-k}
여기서 $P_{n-k}$는 나머지 $n-k$명의 남자가 자신의 모자 중에서 선택할 때 일치가 없는 조건부 확률이다. $k$명의 남자를 선택하는 $\binom{n}{k}$가지 방법이 있으므로, 정확히 $k$개의 일치가 발생할 원하는 확률은 다음과 같다:\frac{P_{n-k}}{k!}=\frac{\frac{1}{2!}-\frac{1}{3!}+\cdots+\frac{(-1)^{n-k}}{(n-k)!}}{k!}
확률 이론에서 중요한 개념은 사건의 **조건부 독립(conditional independence)**이다. 사건 $E_{1}$과 $E_{2}$가 $F$가 주어졌을 때 조건부 독립이라고 말하는 것은, $F$가 발생했을 때 $E_{2}$의 발생 여부에 대한 정보가 $E_{1}$이 발생할 조건부 확률을 변경하지 않는다는 의미이다. 더 형식적으로, $E_{1}$과 $E_{2}$는 $F$가 주어졌을 때 다음과 같은 경우 조건부 독립이라고 한다:P\left(E_{1} \mid E_{2} F\right)=P\left(E_{1} \mid F\right)
P\left(E_{1} E_{2} \mid F\right)=P\left(E_{1} \mid F\right) P\left(E_{2} \mid F\right)
조건부 독립의 개념은 두 개 이상의 사건으로 쉽게 확장될 수 있으며, 이 확장은 연습 문제로 남겨둔다. 독자는 조건부 독립의 개념이 예제 5a에서 암묵적으로 사용되었음을 주목해야 한다. 이 예제에서는 보험 가입자가 $i$번째 해($i=1,2, \ldots$)에 사고를 겪는 사건들이 그 사람이 사고를 잘 내는 경향이 있는지 여부에 따라 조건부 독립이라고 가정되었다. 다음 예제는 때때로 **라플라스의 계승 규칙(Laplace's rule of succession)**이라고 불리며, 조건부 독립의 개념을 더욱 잘 보여준다. ## Example ## Laplace's rule of succession 상자에 $k+1$개의 동전이 있다. $i$번째 동전은 던졌을 때 $i/k$의 확률로 앞면이 나온다 ($i=0,1, \ldots, k$). 상자에서 동전 하나를 무작위로 선택한 다음 반복해서 던진다. 처음 $n$번의 던지기에서 모두 앞면이 나왔다면, $(n+1)$번째 던지기에서도 앞면이 나올 조건부 확률은 얼마인가? 풀이 $i$번째 동전($i=0,1, \ldots, k$)이 처음에 선택되는 사건을 $C_i$라고 하자. 처음 $n$번의 던지기에서 모두 앞면이 나오는 사건을 $F_n$이라고 하고, $(n+1)$번째 던지기에서 앞면이 나오는 사건을 $H$라고 하자. 우리가 구하고자 하는 확률 $P(H \mid F_n)$은 다음과 같이 얻을 수 있다:P\left(H \mid F_{n}\right)=\sum_{i=0}^{k} P\left(H \mid F_{n} C_{i}\right) P\left(C_{i} \mid F_{n}\right)
이제 $i$번째 동전이 선택되었다고 가정하면, 각 던지기 결과는 조건부적으로 독립이며, 각각 $i/k$의 확률로 앞면이 나온다고 가정하는 것이 합리적이다. 따라서,P\left(H \mid F_{n} C_{i}\right)=P\left(H \mid C_{i}\right)=\frac{i}{k}
P\left(C_{i} \mid F_{n}\right)=\frac{P\left(C_{i} F_{n}\right)}{P\left(F_{n}\right)}=\frac{P\left(F_{n} \mid C_{i}\right) P\left(C_{i}\right)}{\sum_{j=0}^{k} P\left(F_{n} \mid C_{j}\right) P\left(C_{j}\right)}=\frac{(i / k)^{n}[1 /(k+1)]}{\sum_{j=0}^{k}(j / k)^{n}[1 /(k+1)]}
P\left(H \mid F_{n}\right)=\frac{\sum_{i=0}^{k}(i / k)^{n+1}}{\sum_{j=0}^{k}(j / k)^{n}}
그러나 $k$가 크다면, 우리는 다음 적분 근사를 사용할 수 있다:\begin{gathered} \frac{1}{k} \sum_{i=0}^{k}\left(\frac{i}{k}\right)^{n+1} \approx \int_{0}^{1} x^{n+1} d x=\frac{1}{n+2} \ \frac{1}{k} \sum_{j=0}^{k}\left(\frac{j}{k}\right)^{n} \approx \int_{0}^{1} x^{n} d x=\frac{1}{n+1} \end{gathered}
따라서 $k$가 클 때,P\left(H \mid F_{n}\right) \approx \frac{n+1}{n+2}
## Example <br> 5f ## Updating information sequentially $n$개의 상호 배타적이고 전체를 포함하는(mutually exclusive and exhaustive) 가설이 있다고 가정하자. 이 가설들의 초기(때로는 **사전(prior) 확률**이라고도 함) 확률은 $P\left(H_{i}\right)$이며, $\sum_{i=1}^{n} P\left(H_{i}\right)=1$이다. 이제 사건 $E$가 발생했다는 정보가 수신되면, $H_{i}$가 참 가설일 조건부 확률(때로는 $H_{i}$의 **갱신된(updated) 확률** 또는 **사후(posterior) 확률**이라고도 함)은 다음과 같다.P\left(H_{i} \mid E\right)=\frac{P\left(E \mid H_{i}\right) P\left(H_{i}\right)}{\sum_{j} P\left(E \mid H_{j}\right) P\left(H_{j}\right)}
이제 $E_{1}$이 발생한 다음 $E_{2}$가 발생했다는 것을 알게 되었다고 가정하자. 그러면 첫 번째 정보만 주어졌을 때, $H_{i}$가 참 가설일 조건부 확률은 다음과 같다.P\left(H_{i} \mid E_{1}\right)=\frac{P\left(E_{1} \mid H_{i}\right) P\left(H_{i}\right)}{P\left(E_{1}\right)}=\frac{P\left(E_{1} \mid H_{i}\right) P\left(H_{i}\right)}{\sum_{j} P\left(E_{1} \mid H_{j}\right) P\left(H_{j}\right)}
반면, 두 가지 정보가 모두 주어졌을 때, $H_{i}$가 참 가설일 조건부 확률은 $P\left(H_{i} \mid E_{1} E_{2}\right)$이며, 이는 다음을 통해 계산할 수 있다.P\left(H_{i} \mid E_{1} E_{2}\right)=\frac{P\left(E_{1} E_{2} \mid H_{i}\right) P\left(H_{i}\right)}{\sum_{j} P\left(E_{1} E_{2} \mid H_{j}\right) P\left(H_{j}\right)}
그러나 $E=E_{2}$로 하고 $P\left(H_{j}\right)$를 $P\left(H_{j} \mid E_{1}\right)$, $j=1, \ldots, n$으로 대체하여 Equation (5.13)의 우변을 사용하여 $P\left(H_{i} \mid E_{1} E_{2}\right)$를 계산할 수 있는지 궁금할 수 있다. 즉, $P\left(H_{j} \mid E_{1}\right)$, $j \geq 1$을 사전 확률로 간주하고 (5.13)을 사용하여 사후 확률을 계산하는 것이 언제 정당한가? 해답은 각 $j= 1, \ldots, n$에 대해 사건 $E_{1}$과 $E_{2}$가 $H_{j}$가 주어졌을 때 **조건부 독립(conditionally independent)**인 경우에 앞선 방법이 정당하다는 것이다. 만약 그렇다면,P\left(E_{1} E_{2} \mid H_{j}\right)=P\left(E_{2} \mid H_{j}\right) P\left(E_{1} \mid H_{j}\right), \quad j=1, \ldots, n
\begin{aligned} P\left(H_{i} \mid E_{1} E_{2}\right) & =\frac{P\left(E_{2} \mid H_{i}\right) P\left(E_{1} \mid H_{i}\right) P\left(H_{i}\right)}{P\left(E_{1} E_{2}\right)} \ & =\frac{P\left(E_{2} \mid H_{i}\right) P\left(E_{1} H_{i}\right)}{P\left(E_{1} E_{2}\right)} \ & =\frac{P\left(E_{2} \mid H_{i}\right) P\left(H_{i} \mid E_{1}\right) P\left(E_{1}\right)}{P\left(E_{1} E_{2}\right)} \ & =\frac{P\left(E_{2} \mid H_{i}\right) P\left(H_{i} \mid E_{1}\right)}{Q(1,2)} \end{aligned}
여기서 $Q(1,2)=\frac{P\left(E_{1} E_{2}\right)}{P\left(E_{1}\right)}$이다. 앞선 방정식이 모든 $i$에 대해 유효하므로, 합산하면 다음을 얻는다.1=\sum_{i=1}^{n} P\left(H_{i} \mid E_{1} E_{2}\right)=\sum_{i=1}^{n} \frac{P\left(E_{2} \mid H_{i}\right) P\left(H_{i} \mid E_{1}\right)}{Q(1,2)}
Q(1,2)=\sum_{i=1}^{n} P\left(E_{2} \mid H_{i}\right) P\left(H_{i} \mid E_{1}\right)
P\left(H_{i} \mid E_{1} E_{2}\right)=\frac{P\left(E_{2} \mid H_{i}\right) P\left(H_{i} \mid E_{1}\right)}{\sum_{i=1}^{n} P\left(E_{2} \mid H_{i}\right) P\left(H_{i} \mid E_{1}\right)}
예를 들어, 두 개의 동전 중 하나를 선택하여 던진다고 가정하자. $H_{i}$를 $i=1,2$인 동전 $i$가 선택되는 사건이라고 하고, 동전 $i$를 던졌을 때 확률 $p_{i}$로 앞면이 나온다고 가정하자. 그러면 앞선 방정식들은 이전 던지기 결과가 주어졌을 때 동전 1이 던져지고 있을 확률을 순차적으로 갱신하기 위해, 매번 새로운 던지기 후에 저장해야 하는 것은 동전 1이 사용되고 있을 조건부 확률뿐임을 보여준다. 즉, 모든 이전 결과를 추적할 필요는 없다. ## Summary 사건 $E$와 $F$에 대해, $F$가 발생했을 때 $E$의 조건부 확률은 $P(E \mid F)$로 표기되며 다음과 같이 정의된다.P(E \mid F)=\frac{P(E F)}{P(F)}
P\left(E_{1} E_{2} \cdots E_{n}\right)=P\left(E_{1}\right) P\left(E_{2} \mid E_{1}\right) \cdots P\left(E_{n} \mid E_{1} \cdots E_{n-1}\right)
P(E)=P(E \mid F) P(F)+P\left(E \mid F^{c}\right) P\left(F^{c}\right)
이것은 $F$가 발생하는지 여부에 "conditioning"하여 $P(E)$를 계산하는 데 사용될 수 있다. $P(H) / P\left(H^{c}\right)$는 사건 $H$의 **오즈(odds)**라고 불린다. 다음 항등식은\frac{P(H \mid E)}{P\left(H^{c} \mid E\right)}=\frac{P(H) P(E \mid H)}{P\left(H^{c}\right) P\left(E \mid H^{c}\right)}
새로운 증거 $E$가 얻어졌을 때, $H$의 오즈 값은 $H$가 참일 때 새로운 증거의 조건부 확률과 $H$가 참이 아닐 때의 조건부 확률의 비율을 이전 값에 곱한 값이 됨을 보여준다. $F_{i}, i=1, \ldots, n$를 합집합이 전체 표본 공간인 **상호 배타적인 사건(mutually exclusive events)**이라고 하자. 다음 항등식은 ## Problems 3.1. 두 개의 공정한 주사위를 굴린다. 주사위가 서로 다른 숫자로 나왔을 때, 적어도 하나가 6이 나올 조건부 확률은 얼마인가? 3.2. 두 개의 공정한 주사위를 굴렸을 때, 주사위의 합이 $i$일 때 첫 번째 주사위가 6이 나올 조건부 확률은 얼마인가? $i$가 2에서 12 사이의 모든 값에 대해 계산하시오.P\left(F_{j} \mid E\right)=\frac{P\left(E \mid F_{j}\right) P\left(F_{j}\right)}{\sum_{i=1}^{n} P\left(E \mid F_{i}\right) P\left(F_{i}\right)}
는 **Bayes's formula**로 알려져 있다. 만약 사건 $F_{i}, i=1, \ldots, n$이 경쟁 가설이라면, Bayes's formula는 추가적인 증거 $E$가 있을 때 이 가설들의 조건부 확률을 계산하는 방법을 보여준다. Bayes's formula의 분모는 다음을 사용한다.P(E)=\sum_{i=1}^{n} P\left(E \mid F_{i}\right) P\left(F_{i}\right)
이는 **law of total probability**라고 불린다. 만약 $P(E F)=P(E) P(F)$이면, 우리는 사건 $E$와 $F$가 **independent**라고 말한다. 이 조건은 $P(E \mid F)=P(E)$ 및 $P(F \mid E)=P(F)$와 동등하다. 따라서 사건 $E$와 $F$는 한 사건의 발생에 대한 지식이 다른 사건의 확률에 영향을 미치지 않을 때 independent이다. 사건 $E_{1}, \ldots, E_{n}$은 그들의 어떤 부분집합 $E_{i_{1}}, \ldots, E_{i_{r}}$에 대해서도 다음이 성립할 때 **independent**라고 한다.P\left(E_{i_{1}} \cdots E_{i_{r}}\right)=P\left(E_{i_{1}}\right) \cdots P\left(E_{i_{r}}\right)
고정된 사건 $F$에 대해, $P(E \mid F)$는 표본 공간의 사건 $E$에 대한 확률 함수로 간주될 수 있다. 3.3. Equation (2.1)을 사용하여 브리지 게임에서 North와 South가 스페이드 합계 8장을 가지고 있을 때, East가 스페이드 3장을 가질 조건부 확률을 계산하시오. 3.4. 한 쌍의 공정한 주사위를 굴렸을 때, 주사위의 합이 $i$일 때(단, $i=2,3, \ldots, 12$) 적어도 하나가 6이 나올 확률은 얼마인가? 3.5. 항아리에 흰 공 6개와 검은 공 9개가 들어 있다. 4개의 공을 비복원 추출로 무작위로 선택할 때, 처음 2개가 흰 공이고 마지막 2개가 검은 공일 확률은 얼마인가? 3.6. 흰 공 8개가 포함된 총 12개의 공이 들어 있는 항아리를 고려하시오. 크기 4의 표본을 복원 추출(비복원 추출)로 뽑을 것이다. 뽑힌 표본에 정확히 3개의 흰 공이 포함되어 있을 때, 뽑힌 첫 번째와 세 번째 공이 흰 공일 조건부 확률은 (각 경우에 대해) 얼마인가? 3.7. 왕은 2명의 자녀를 둔 가족 출신이다. 다른 자녀가 그의 여동생일 확률은 얼마인가? 3.8. 한 부부에게 2명의 자녀가 있다. 두 자녀 중 나이가 많은 자녀가 딸일 때, 두 자녀 모두 딸일 확률은 얼마인가? 3.9. 3개의 항아리를 고려하시오. 항아리 $A$에는 흰 공 2개와 빨간 공 4개, 항아리 $B$에는 흰 공 8개와 빨간 공 4개, 항아리 $C$에는 흰 공 1개와 빨간 공 3개가 들어 있다. 각 항아리에서 공을 1개씩 선택할 때, 정확히 2개의 흰 공이 선택되었을 때 항아리 $A$에서 선택된 공이 흰 공일 확률은 얼마인가? 3.10. 52장의 일반적인 플레잉 카드 덱에서 3장의 카드를 비복원 추출로 무작위로 선택한다. 두 번째와 세 번째 카드가 스페이드일 때, 첫 번째 카드가 스페이드일 조건부 확률을 계산하시오. 3.11. 52장의 일반적인 카드 덱에서 2장의 카드를 비복원 추출로 무작위로 선택한다. $B$를 두 카드 모두 에이스인 사건, $A_{s}$를 스페이드 에이스가 선택된 사건, $A$를 적어도 하나의 에이스가 선택된 사건이라고 하자. 다음을 구하시오. (a) $P\left(B \mid A_{s}\right)$ (b) $P(B \mid A)$ 3.12. 최근 대학을 졸업한 한 학생이 다가오는 여름에 처음 세 번의 보험계리사 시험을 치를 계획이다. 그녀는 6월에 첫 번째 보험계리사 시험을 치를 것이다. 그 시험에 합격하면 7월에 두 번째 시험을 치르고, 그 시험에도 합격하면 9월에 세 번째 시험을 치를 것이다. 시험에 불합격하면 다른 시험을 치를 수 없다. 그녀가 첫 번째 시험에 합격할 확률은 .9이다. 첫 번째 시험에 합격하면 두 번째 시험에 합격할 조건부 확률은 .8이고, 첫 번째와 두 번째 시험 모두 합격하면 세 번째 시험에 합격할 조건부 확률은 .7이다. (a) 그녀가 세 시험 모두 합격할 확률은 얼마인가? (b) 그녀가 세 시험 모두 합격하지 못했을 때, 그녀가 두 번째 시험에 불합격했을 조건부 확률은 얼마인가? 3.13. 52장의 일반적인 카드 덱(에이스 4장 포함)이 무작위로 각각 13장씩 4개의 패로 나뉜다고 가정하자. 우리는 각 패에 에이스가 하나씩 있을 확률 $p$를 구하는 데 관심이 있다. $E_{i}$를 $i$번째 패에 정확히 하나의 에이스가 있는 사건이라고 하자. 곱셈 규칙을 사용하여 $p= P\left(E_{1} E_{2} E_{3} E_{4}\right)$를 구하시오. 3.14. 항아리에는 처음에 흰 공 5개와 검은 공 7개가 들어 있다. 공을 선택할 때마다 색깔을 확인하고, 같은 색깔의 공 2개와 함께 항아리에 다시 넣는다. 다음 확률을 계산하시오. (a) 처음 2개의 공이 검은색이고 다음 2개가 흰색일 확률 (b) 처음 4개의 공 중 정확히 2개가 검은색일 확률 3.15. 자궁외 임신은 임산부가 흡연자일 때 비흡연자일 때보다 두 배 더 발생할 가능성이 높다. 가임기 여성의 32%가 흡연자라면, 자궁외 임신을 겪는 여성 중 흡연자의 비율은 얼마인가? 3.16. 모든 아기의 98%는 출산 후 생존한다. 그러나 모든 출산의 15%는 제왕절개(C-section)를 포함하며, 제왕절개를 했을 때 아기가 생존할 확률은 96%이다. 무작위로 선택된 임산부가 제왕절개를 하지 않았을 때, 그녀의 아기가 생존할 확률은 얼마인가? 3.17. 특정 지역사회에서 가족의 36%가 개를 소유하고 있으며, 개를 소유한 가족의 22%는 고양이도 소유하고 있다. 또한, 가족의 30%가 고양이를 소유하고 있다. 다음을 구하시오. (a) 무작위로 선택된 가족이 개와 고양이를 모두 소유할 확률 (b) 무작위로 선택된 가족이 고양이를 소유하고 있을 때, 개를 소유할 조건부 확률 3.18. 특정 도시의 유권자 중 총 46%는 자신을 무소속으로 분류하고, 30%는 자유주의자로 분류하며, 24%는 보수주의자라고 말한다. 최근 지역 선거에서 무소속 유권자의 35%, 자유주의자 유권자의 62%, 보수주의자 유권자의 58%가 투표했다. 한 유권자가 무작위로 선택되었다. 이 사람이 지역 선거에 투표했다고 가정할 때, 그 또는 그녀가 다음일 확률은 얼마인가? (a) 무소속 유권자 (b) 자유주의자 유권자 (c) 보수주의자 유권자 (d) 지역 선거에 참여한 유권자의 비율은 얼마인가? 3.19. 특정 "금연" 수업을 들은 여성의 48%와 남성의 37%가 수업을 마친 후 최소 1년 동안 비흡연자로 남았다. 이들은 1년 후 성공 파티에 참석했다. 원래 수업의 62%가 남성이었다면, (a) 파티에 참석한 사람들 중 여성의 비율은 얼마인가? (b) 원래 수업의 몇 퍼센트가 파티에 참석했는가? 3.20. 특정 대학 학생의 52%는 여성이다. 이 대학 학생의 5%는 컴퓨터 과학을 전공하고 있다. 학생의 2%는 컴퓨터 과학을 전공하는 여성이다. 한 학생이 무작위로 선택되었을 때, 다음 조건부 확률을 구하시오. (a) 학생이 컴퓨터 과학을 전공하고 있을 때, 그 학생이 여성일 확률 (b) 학생이 여성일 때, 그 학생이 컴퓨터 과학을 전공하고 있을 확률 3.21. 500쌍의 결혼한 맞벌이 부부를 대상으로 연봉에 대해 설문조사를 실시한 결과는 다음과 같다. | | 남편 | | | :--- | :---: | :---: | | 아내 | $\$25,000$ 미만 | $\$25,000$ 초과 | | $\$25,000$ 미만 | 212 | 198 | | $\$25,000$ 초과 | 36 | 54 | 예를 들어, 36쌍의 부부에서 아내는 $\$25,000$ 이상을 벌고 남편은 $\$25,000$ 미만을 벌었다. 이 부부 중 한 쌍이 무작위로 선택되었을 때, 다음을 구하시오. (a) 남편이 $\$25,000$ 미만을 벌 확률 (b) 남편이 이 금액 이상을 벌었을 때, 아내가 $\$25,000$ 이상을 벌 조건부 확률 (c) 남편이 이 금액 미만을 벌었을 때, 아내가 $\$25,000$ 이상을 벌 조건부 확률 3.22. 빨간 주사위, 파란 주사위, 노란 주사위(모두 6면체)를 굴린다. 우리는 파란 주사위에 나타난 숫자가 노란 주사위에 나타난 숫자보다 작고, 노란 주사위에 나타난 숫자가 빨간 주사위에 나타난 숫자보다 작을 확률에 관심이 있다. 즉, 파란색, 노란색, 빨간색 주사위에 나타난 숫자를 각각 $B, Y, R$이라고 할 때, 우리는 $P(B<Y<R)$에 관심이 있다. (a) 어떤 두 주사위도 같은 숫자가 나오지 않을 확률은 얼마인가? (b) 어떤 두 주사위도 같은 숫자가 나오지 않았을 때, $B<Y<R$일 조건부 확률은 얼마인가? (c) $P(B<Y<R)$은 얼마인가? 3.23. 항아리 I에는 흰 공 2개와 빨간 공 4개가 들어 있고, 항아리 II에는 흰 공 1개와 빨간 공 1개가 들어 있다. 항아리 I에서 공을 무작위로 선택하여 항아리 II에 넣은 다음, 항아리 II에서 공을 무작위로 선택한다. 다음을 구하시오. (a) 항아리 II에서 선택된 공이 흰 공일 확률 (b) 항아리 II에서 흰 공이 선택되었을 때, 옮겨진 공이 흰 공이었을 조건부 확률 3.24. 2개의 공 각각은 검은색 또는 금색으로 칠해진 다음 항아리에 넣어졌다. 각 공이 확률 $\frac{1}{2}$로 검은색으로 칠해지고 이 사건들이 독립적이라고 가정하자. (a) 금색 페인트가 사용되었다는 정보(따라서 적어도 하나의 공이 금색으로 칠해져 있음)를 얻었다고 가정하자. 두 공 모두 금색으로 칠해져 있을 조건부 확률을 계산하시오. (b) 이제 항아리가 넘어져 공 1개가 굴러 나왔다고 가정하자. 그 공은 금색으로 칠해져 있다. 이 경우 두 공 모두 금색일 확률은 얼마인가? 설명하시오. 3.25. 인구 100,000명인 마을에 거주하는 50세 이상 인구수를 추정하기 위해 다음과 같은 방법이 제안되었다: "거리를 걸으면서 만나는 사람들 중 50세 이상인 사람들의 비율을 계속해서 세어라. 며칠 동안 이렇게 한 다음, 얻은 비율에 100,000을 곱하여 추정치를 얻어라." 이 방법에 대해 논평하시오. 힌트: $p$를 마을에서 50세 이상인 사람들의 비율이라고 하자. 또한, $\alpha_{1}$을 50세 미만인 사람이 거리에서 보내는 시간의 비율이라고 하고, $\alpha_{2}$를 50세 이상인 사람에 대한 해당 값이라고 하자. 제안된 방법이 추정하는 양은 무엇인가? 추정치가 $p$와 대략적으로 같을 때는 언제인가? 3.26. 남성의 5%와 여성의 0.25%가 색맹이라고 가정하자. 색맹인 사람이 무작위로 선택되었다. 이 사람이 남성일 확률은 얼마인가? 남성과 여성의 수가 같다고 가정하자. 만약 인구가 남성이 여성보다 두 배 많다면 어떻게 될까? 3.27. 특정 회사의 모든 직원은 차를 몰고 출근하여 회사 주차장에 주차한다. 회사는 자동차 한 대당 평균 직원 수를 추정하는 데 관심이 있다. 다음 방법 중 어떤 방법이 이 양을 추정하는 데 도움이 될까? 답을 설명하시오. 1. $n$명의 직원을 무작위로 선택하고, 그들이 타고 온 차에 몇 명이 있었는지 알아낸 다음, $n$개의 값의 평균을 취한다. 2. 주차장에 있는 $n$대의 차를 무작위로 선택하고, 그 차에 몇 명이 타고 왔는지 알아낸 다음, $n$개의 값의 평균을 취한다. 3.28. 52장의 일반적인 카드 덱이 섞인 다음, 첫 번째 에이스가 나타날 때까지 카드를 한 장씩 뒤집는다고 가정하자. 첫 번째 에이스가 20번째로 나타난 카드라고 가정할 때, 그 다음 카드가 다음일 조건부 확률은 얼마인가? (a) 스페이드 에이스 (b) 클럽 2 3.29. 상자 안에 테니스 공 15개가 들어 있는데, 그 중 9개는 이전에 사용되지 않았다. 공 3개를 무작위로 선택하여 사용한 다음 상자에 다시 넣는다. 나중에 상자에서 다른 공 3개를 무작위로 선택한다. 이 공들 중 어느 것도 사용된 적이 없을 확률을 구하시오. 3.30. 두 개의 상자를 고려하시오. 하나는 검은색 구슬 1개와 흰색 구슬 1개, 다른 하나는 검은색 구슬 2개와 흰색 구슬 1개를 포함한다. 상자를 무작위로 선택하고, 그 상자에서 구슬을 무작위로 뽑는다. 구슬이 검은색일 확률은 얼마인가? 구슬이 흰색일 때 첫 번째 상자가 선택되었을 확률은 얼마인가? 3.31. 아퀴나 씨는 암일 가능성이 있는 종양에 대한 생검을 막 마쳤다. 주말 가족 행사를 망치고 싶지 않아, 그녀는 며칠 동안 나쁜 소식을 듣고 싶지 않다. 그러나 의사에게 좋은 소식일 때만 전화하라고 말하면, 의사가 전화하지 않을 경우 아퀴나 씨는 소식이 나쁘다고 결론 내릴 수 있다. 그래서 확률을 공부하는 학생인 아퀴나 씨는 의사에게 동전을 던지라고 지시한다. 앞면이 나오면 의사는 좋은 소식일 때 전화하고 나쁜 소식일 때 전화하지 않는다. 뒷면이 나오면 의사는 전화하지 않는다. 이런 식으로 의사가 전화하지 않더라도 소식이 반드시 나쁜 것은 아니다. $\alpha$를 종양이 암일 확률이라고 하고, $\beta$를 의사가 전화하지 않았을 때 종양이 암일 조건부 확률이라고 하자. (a) $\alpha$와 $\beta$ 중 어느 것이 더 커야 하는가? (b) $\beta$를 $\alpha$로 표현하고, (a) 부분의 답을 증명하시오. 3.32. 한 가족이 확률 $p_{j}$로 $j$명의 자녀를 갖는다고 가정하자. 여기서 $p_{1}=.1, p_{2}=.25, p_{3}=.35, p_{4}=.3$이다. 이 가족의 자녀 중 한 명이 무작위로 선택되었다. 이 자녀가 가족의 맏이일 때, 가족이 다음을 가질 조건부 확률을 구하시오. (a) 자녀가 1명뿐일 확률 (b) 자녀가 4명일 확률 무작위로 선택된 자녀가 가족의 막내일 때 (a)와 (b)를 다시 계산하시오. 3.33. 비 오는 날 Joe는 확률 .3으로 지각하고, 비 오지 않는 날에는 확률 .1로 지각한다. 내일 비가 올 확률은 .7이다. (a) Joe가 내일 일찍 올 확률을 구하시오. (b) Joe가 일찍 왔을 때, 비가 왔을 조건부 확률은 얼마인가? 3.34. 예제 3f에서, 새로운 증거가 다른 가능한 해석을 가질 수 있으며, 실제로 범인이 해당 특성을 가질 확률이 90%임을 보여준다고 가정하자. 이 경우, 용의자가 유죄일 가능성은 얼마나 될까(이전과 같이 그가 그 특성을 가지고 있다고 가정)? 3.35. 확률 .6으로 엄마가 선물을 숨겼고, 확률 .4로 아빠가 선물을 숨겼다. 엄마가 선물을 숨길 때, 70%는 위층에, 30%는 아래층에 숨긴다. 아빠는 위층이나 아래층에 똑같이 숨길 가능성이 있다. (a) 선물이 위층에 있을 확률은 얼마인가? (b) 선물이 아래층에 있을 때, 아빠가 숨겼을 확률은 얼마인가? 3.36. 상점 $A, B, C$는 각각 50, 75, 100명의 직원을 가지고 있으며, 그 중 각각 50%, 60%, 70%가 여성이다. 성별에 관계없이 모든 직원들 사이에서 사직은 똑같이 발생할 가능성이 있다. 한 여성 직원이 사직했다. 그녀가 상점 $C$에서 일할 확률은 얼마인가? 3.37. (a) 도박꾼이 주머니에 공정한 동전과 양면이 앞면인 동전을 가지고 있다. 그는 동전 중 하나를 무작위로 선택하고, 그것을 던졌을 때 앞면이 나온다. 그것이 공정한 동전일 확률은 얼마인가? (b) 그가 같은 동전을 두 번째 던졌을 때, 다시 앞면이 나왔다고 가정하자. 이제 그것이 공정한 동전일 확률은 얼마인가? (c) 그가 같은 동전을 세 번째 던졌을 때 뒷면이 나왔다고 가정하자. 이제 그것이 공정한 동전일 확률은 얼마인가? 3.38. 항아리 $A$에는 흰 공 5개와 검은 공 7개가 들어 있다. 항아리 $B$에는 흰 공 3개와 검은 공 12개가 들어 있다. 우리는 공정한 동전을 한 번 던진다. 결과가 앞면이면 항아리 $A$에서 공을 선택하고, 뒷면이면 항아리 $B$에서 공을 선택한다. 흰 공이 선택되었다고 가정하자. 동전이 뒷면으로 나왔을 확률은 얼마인가? 3.39. 예제 3a에서, 첫 해에 사고가 없었을 때 두 번째 해에 사고가 날 확률은 얼마인가? 3.40. 다음과 같은 방식으로 추출된 크기 3의 표본을 고려하시오. 흰 공 5개와 빨간 공 7개가 들어 있는 항아리에서 시작한다. 각 단계에서 공을 뽑고 색깔을 확인한다. 그런 다음 공은 같은 색깔의 공 하나와 함께 항아리에 다시 넣어 진다. 표본에 정확히 다음이 포함될 확률을 구하시오. (a) 흰 공 0개 (b) 흰 공 1개 (c) 흰 공 3개 (d) 흰 공 2개 3.41. 카드 덱이 섞인 다음 각각 26장의 카드 두 묶음으로 나뉜다. 한 묶음에서 카드를 뽑았는데 에이스로 밝혀졌다. 그 에이스는 두 번째 묶음에 넣어 진다. 그런 다음 그 묶음이 섞이고, 그 묶음에서 카드를 뽑는다. 이 뽑힌 카드가 에이스일 확률을 계산하시오. 힌트: 교환된 카드가 선택되었는지 여부에 따라 조건화하시오. 3.42. 모든 미국 가구의 12%는 캘리포니아에 있다. 모든 미국 가구의 총 1.3%는 연간 $\$250,000$ 이상을 벌고, 모든 캘리포니아 가구의 총 3.3%는 연간 $\$250,000$ 이상을 번다. (a) 캘리포니아 이외의 모든 가구 중 연간 $\$250,000$ 이상을 버는 비율은 얼마인가? (b) 무작위로 선택된 미국 가구가 연간 $\$250,000$ 이상을 번다고 가정할 때, 그 가구가 캘리포니아 가구일 확률은 얼마인가? 3.43. 상자 안에 동전 3개가 들어 있다. 하나는 양면이 앞면인 동전이고, 다른 하나는 공정한 동전이며, 세 번째는 75% 확률로 앞면이 나오는 편향된 동전이다. 3개의 동전 중 하나를 무작위로 선택하여 던졌을 때 앞면이 나왔다. 그것이 양면이 앞면인 동전이었을 확률은 얼마인가? 3.44. 세 명의 죄수가 간수로부터 그들 중 한 명이 무작위로 선택되어 처형되고 나머지 두 명은 풀려날 것이라는 통보를 받았다. 죄수 $A$는 간수에게 동료 죄수 중 누가 풀려날지 개인적으로 알려달라고 요청하며, 이미 두 명 중 적어도 한 명은 풀려날 것을 알고 있으므로 이 정보를 누설해도 해가 없을 것이라고 주장한다. 간수는 $A$가 동료 죄수 중 누가 풀려날지 알게 되면, 그가 두 명의 죄수 중 한 명이 될 것이므로 자신의 처형 확률이 $\frac{1}{3}$에서 $\frac{1}{2}$로 증가할 것이라고 지적하며 질문에 답하기를 거부한다. 간수의 추론에 대해 어떻게 생각하는가? 3.45. $i$번째 동전을 던졌을 때 앞면이 나올 확률이 $i/10$인 10개의 동전이 있다고 가정하자. 여기서 $i= 1,2, \ldots, 10$이다. 동전 중 하나를 무작위로 선택하여 던졌을 때 앞면이 나왔다. 그것이 다섯 번째 동전이었을 조건부 확률은 얼마인가? 3.46. 특정 연도에 남성 자동차 보험 가입자는 확률 $p_{m}$으로 청구를 하고, 여성 보험 가입자는 확률 $p_{f}$로 청구를 한다. 여기서 $p_{f} \neq p_{m}$이다. 보험 가입자 중 남성의 비율은 $\alpha, 0<\alpha<1$이다. 한 보험 가입자가 무작위로 선택되었다. $A_{i}$를 이 보험 가입자가 $i$년에 청구를 할 사건이라고 할 때, 다음을 보이시오.P\left(A_{2} \mid A_{1}\right)>P\left(A_{1}\right)
위 부등식이 참인 이유에 대한 직관적인 설명을 제시하시오. 3.47. 항아리에는 흰 공 5개와 검은 공 10개가 들어 있다. 공정한 주사위를 굴리고, 그 숫자만큼의 공을 항아리에서 무작위로 선택한다. 선택된 공이 모두 흰 공일 확률은 얼마인가? 선택된 공이 모두 흰 공일 때 주사위가 3에 나왔을 조건부 확률은 얼마인가? 3.48. 외관이 동일한 2개의 캐비닛 각각에는 2개의 서랍이 있다. 캐비닛 $A$에는 각 서랍에 은화가 들어 있고, 캐비닛 $B$에는 한 서랍에 은화가, 다른 서랍에 금화가 들어 있다. 캐비닛이 무작위로 선택되고, 그 중 한 서랍이 열렸는데 은화가 발견되었다. 다른 서랍에 은화가 있을 확률은 얼마인가? 3.49. 전립선암은 남성에게서 발견되는 가장 흔한 유형의 암이다. 남성이 전립선암에 걸렸는지 여부를 나타내는 지표로, 의사들은 종종 전립선에서만 생성되는 전립선 특이 항원(PSA) 수치를 측정하는 검사를 수행한다. PSA 수치는 암을 나타내지만, 이 검사는 신뢰할 수 없기로 악명이 높다. 실제로 암이 없는 남성이 PSA 수치가 상승할 확률은 약 .135이며, 남성이 암에 걸렸을 경우 약 .268로 증가한다. 다른 요인들을 바탕으로 의사가 남성이 전립선암에 걸렸을 확률이 70%라고 확신할 때, 다음 조건부 확률은 얼마인가? (a) 검사 결과 PSA 수치가 상승했다고 나타났을 때, 그가 암에 걸렸을 확률 (b) 검사 결과 PSA 수치가 상승했다고 나타나지 않았을 때, 그가 암에 걸렸을 확률 이번에는 의사가 처음에 남성이 전립선암에 걸렸을 확률이 30%라고 믿는다고 가정하고 위 계산을 반복하시오. 3.50. 보험 회사가 사람들을 세 가지 등급으로 분류한다고 가정하자: 우량 위험, 보통 위험, 불량 위험. 회사의 기록에 따르면 우량, 보통, 불량 위험군이 1년 동안 사고에 연루될 확률은 각각 .05, .15, .30이다. 인구의 20%가 우량 위험군이고, 50%가 보통 위험군이며, 30%가 불량 위험군이라면, 특정 연도에 사고를 겪는 사람들의 비율은 얼마인가? 보험 가입자 $A$가 2012년에 사고가 없었다면, 그 또는 그녀가 우량 위험군일 확률은 얼마인가? 보통 위험군일 확률은 얼마인가? 3.51. 한 직원이 상사에게 새 직장을 위한 추천서를 요청했다. 그녀는 강력한 추천서를 받으면 직장을 얻을 확률이 80%, 적당히 좋은 추천서를 받으면 40%, 약한 추천서를 받으면 10%라고 추정한다. 그녀는 또한 추천서가 강력할 확률, 보통일 확률, 약할 확률이 각각 .7, .2, .1이라고 추정한다. (a) 그녀는 새 직장 제안을 받을 것이라고 얼마나 확신하는가? (b) 그녀가 제안을 받았을 때, 그녀는 강력한 추천서를 받았다고 얼마나 생각해야 하는가? 보통 추천서? 약한 추천서? (c) 그녀가 직장 제안을 받지 못했을 때, 그녀는 강력한 추천서를 받았다고 얼마나 생각해야 하는가? 보통 추천서? 약한 추천서? 3.52. 한 고등학생이 특정 대학에 합격했는지 여부를 알려주는 우편물을 초조하게 기다리고 있다. 그녀는 합격했을 때와 불합격했을 때 다음 주 각 요일에 통지를 받을 조건부 확률을 다음과 같이 추정한다. | 요일 | $P$ (우편물\|합격) | $P$ (우편물\|불합격) | | :--- | :---: | :---: | | 월요일 | .15 | .05 | | 화요일 | .20 | .10 | | 수요일 | .25 | .10 | | 목요일 | .15 | .15 | | 금요일 | .10 | .20 | 그녀는 합격할 확률이 .6이라고 추정한다. (a) 그녀가 월요일에 우편물을 받을 확률은 얼마인가? (b) 그녀가 월요일에 우편물을 받지 못했을 때, 화요일에 우편물을 받을 조건부 확률은 얼마인가? (c) 수요일까지 우편물이 오지 않았다면, 그녀가 합격할 조건부 확률은 얼마인가? (d) 목요일에 우편물이 온다면, 그녀가 합격할 조건부 확률은 얼마인가? (e) 그 주에 우편물이 전혀 오지 않는다면, 그녀가 합격할 조건부 확률은 얼마인가? 3.53. 병렬 시스템은 구성 요소 중 적어도 하나가 작동할 때 작동한다. $n$개의 구성 요소로 이루어진 병렬 시스템을 고려하고, 각 구성 요소가 독립적으로 확률 $\frac{1}{2}$로 작동한다고 가정하자. 시스템이 작동하고 있을 때 구성 요소 1이 작동할 조건부 확률을 구하시오. 3.54. (a)부터 (e)까지 설명된 사건 $E$와 $F$에 대한 수학적 모델을 구성해야 한다면, 이들이 독립적인 사건이라고 가정하겠는가? 당신의 추론을 설명하시오. (a) $E$는 사업가가 파란 눈을 가질 사건이고, $F$는 그녀의 비서가 파란 눈을 가질 사건이다. (b) $E$는 교수가 차를 소유할 사건이고, $F$는 그가 전화번호부에 등재될 사건이다. (c) $E$는 남자가 키가 6피트 미만일 사건이고, $F$는 그가 200파운드 이상 나갈 사건이다. (d) $E$는 여자가 미국에 살 사건이고, $F$는 그녀가 서반구에 살 사건이다. (e) $E$는 내일 비가 올 사건이고, $F$는 모레 비가 올 사건이다. 3.55. 한 학급에 1학년 남학생 4명, 1학년 여학생 6명, 2학년 남학생 6명이 있다. 학생을 무작위로 선택했을 때 성별과 학년이 독립적이려면 2학년 여학생이 몇 명 있어야 하는가? 3.56. 쿠폰을 계속 수집하고 있으며 $m$가지 다른 유형이 있다고 가정하자. 또한 새로운 쿠폰을 얻을 때마다 확률 $p_{i}$로 유형 $i$ 쿠폰이라고 가정하자. 여기서 $i=1, \ldots, m$이다. 방금 $n$번째 쿠폰을 수집했다고 가정하자. 그것이 새로운 유형일 확률은 얼마인가? 힌트: 이 쿠폰의 유형에 따라 조건화하시오. 3.57. 주식 가격 움직임에 대한 단순화된 모델은 매일 주식 가격이 확률 $p$로 1단위 상승하거나 확률 $1-p$로 1단위 하락한다고 가정한다. 다른 날의 변화는 독립적이라고 가정한다. (a) 2일 후 주식이 원래 가격에 있을 확률은 얼마인가? (b) 3일 후 주식 가격이 1단위 상승할 확률은 얼마인가? (c) 3일 후 주식 가격이 1단위 상승했다고 가정할 때, 첫째 날에 상승했을 확률은 얼마인가? 3.58. 공정한 동전 던지기의 결과를 생성하고 싶지만, 우리가 사용할 수 있는 것은 앞면이 나올 확률 $p$가 $\frac{1}{2}$과 같을 필요가 없는 편향된 동전뿐이라고 가정하자. 우리의 작업을 수행하기 위한 다음 절차를 고려하시오. 1. 동전을 던진다. 2. 동전을 다시 던진다. 3. 두 번 모두 앞면이 나오거나 두 번 모두 뒷면이 나오면 1단계로 돌아간다. 4. 마지막 던지기의 결과를 실험의 결과로 한다. (a) 결과가 앞면 또는 뒷면이 나올 확률이 같음을 보이시오. (b) 마지막 두 번의 던지기가 다를 때까지 동전을 계속 던진 다음 마지막 던지기의 결과를 결과로 하는 더 간단한 절차를 사용할 수 있을까? 3.59. 확률 $p$로 앞면이 나오는 동전을 독립적으로 던진다. 처음 네 번의 결과가 다음일 확률은 얼마인가? (a) $H, H, H, H$ (b) $T, H, H, H$ (c) 패턴 $T, H, H, H$가 패턴 $H, H, H, H$보다 먼저 나타날 확률은 얼마인가? (c) 부분에 대한 힌트: 패턴 $H, H, H, H$가 어떻게 먼저 나타날 수 있는가? 3.60. 사람의 눈 색깔은 한 쌍의 유전자에 의해 결정된다. 둘 다 파란 눈 유전자이면 파란 눈을 갖게 되고, 둘 다 갈색 눈 유전자이면 갈색 눈을 갖게 되며, 하나는 파란 눈 유전자이고 다른 하나는 갈색 눈 유전자이면 갈색 눈을 갖게 된다. (후자의 사실 때문에 우리는 갈색 눈 유전자가 파란 눈 유전자보다 우성이라고 말한다.) 신생아는 부모 각각으로부터 독립적으로 하나의 눈 유전자를 받으며, 부모로부터 받는 유전자는 그 부모의 두 눈 유전자 중 하나일 가능성이 똑같다. 스미스와 그의 부모 모두 갈색 눈을 가졌지만, 스미스의 여동생은 파란 눈을 가졌다고 가정하자. (a) 스미스가 파란 눈 유전자를 가질 확률은 얼마인가? (b) 스미스의 아내가 파란 눈을 가졌다고 가정하자. 그들의 첫째 아이가 파란 눈을 가질 확률은 얼마인가? (c) 그들의 첫째 아이가 갈색 눈을 가졌다면, 그들의 다음 아이도 갈색 눈을 가질 확률은 얼마인가? 3.61. 백색증과 관련된 유전자는 $A$와 $a$로 표시된다. 양쪽 부모로부터 $a$ 유전자를 받은 사람만이 백색증이 된다. 유전자 쌍 $A, a$를 가진 사람은 겉모습은 정상이며, 자손에게 형질을 물려줄 수 있으므로 **보인자(carrier)**라고 불린다. 정상적인 부부가 두 자녀를 가졌는데, 그 중 정확히 한 명이 백색증이라고 가정하자. 백색증이 아닌 자녀가 백색증 보인자로 알려진 사람과 짝을 이룬다고 가정하자. (a) 그들의 첫째 자손이 백색증일 확률은 얼마인가? (b) 그들의 첫째 자손이 백색증이 아닐 때, 그들의 둘째 자손이 백색증일 조건부 확률은 얼마인가? 3.62. 바바라와 다이앤은 사격 연습을 간다. 바바라의 각 발은 확률 $p_{1}$로 나무 오리 표적을 맞히고, 다이앤의 각 발은 확률 $p_{2}$로 맞힌다고 가정하자. 그들이 동시에 같은 표적을 쏜다고 가정하자. 나무 오리가 쓰러졌을 때(맞았음을 나타냄), 다음 확률은 얼마인가? (a) 두 발 모두 오리를 맞혔을 확률 (b) 바바라의 총알이 오리를 맞혔을 확률 어떤 독립성 가정을 했는가? 3.63. $A$와 $B$는 결투를 벌인다. 결투 규칙은 그들이 총을 들고 동시에 서로를 쏘는 것이다. 한 명 또는 두 명 모두 맞으면 결투는 끝난다. 두 발 모두 빗나가면 과정을 반복한다. 총알의 결과는 독립적이며, $A$의 각 총알은 확률 $p_{A}$로 $B$를 맞히고, $B$의 각 총알은 확률 $p_{B}$로 $A$를 맞힌다고 가정하자. 다음을 구하시오. (a) $A$가 맞지 않을 확률 (b) 두 결투사 모두 맞을 확률 (c) 결투가 $n$번째 총격전 후에 끝날 확률 (d) $A$가 맞지 않았을 때 결투가 $n$번째 총격전 후에 끝날 조건부 확률 (e) 두 결투사 모두 맞았을 때 결투가 $n$번째 총격전 후에 끝날 조건부 확률 3.64. 퀴즈 쇼에서 부부 팀에게 참/거짓 질문이 주어질 것이다. 남편과 아내 모두 독립적으로 확률 $p$로 정답을 맞힐 것이다. 다음 중 부부에게 더 나은 전략은 무엇인가? (a) 둘 중 한 명을 선택하여 그 사람이 질문에 답하게 한다. (b) 둘 다 질문을 고려하게 한 다음, 동의하면 공통된 답을 제시하고, 동의하지 않으면 동전을 던져 어떤 답을 줄지 결정한다. 3.65. 예제 3h에서와 같이, 쌍둥이의 64%가 같은 성별이라고 가정하자. 신생아 쌍둥이가 같은 성별일 때, 그 쌍둥이가 일란성일 조건부 확률은 얼마인가? 3.66. 그림 3.4에 표시된 회로에서 $i$번째 릴레이가 닫힐 확률은 $p_{i}, i=1,2,3,4,5$로 주어진다. 모든 릴레이가 독립적으로 작동한다면, 각 회로에 대해 $A$와 $B$ 사이에 전류가 흐를 확률은 얼마인가?  Figure 3.4 Circuits for Problem 3.66. (b)에 대한 힌트: 릴레이 3이 닫히는지 여부에 따라 조건화하시오. 3.67. $n$개의 구성 요소로 이루어진 공학 시스템은 $n$개의 구성 요소 중 적어도 $k$개가 작동할 때만 시스템이 작동하는 경우 $k$-out-of-$n$ 시스템($k \leq n$)이라고 한다. 모든 구성 요소가 서로 독립적으로 작동한다고 가정하자. (a) $i$번째 구성 요소가 확률 $P_{i}, i= 1,2,3,4$로 작동할 때, 2-out-of-4 시스템이 작동할 확률을 계산하시오. (b) 3-out-of-5 시스템에 대해 (a) 부분을 반복하시오. (c) 모든 $P_{i}$가 $p$와 같을 때($P_{i}=p, i=1,2, \ldots, n$) $k$-out-of-$n$ 시스템에 대해 반복하시오. 3.68. 문제 3.66a에서, $A$에서 $B$로 전류가 흐를 때 릴레이 1과 2가 모두 닫혀 있을 조건부 확률을 구하시오. 3.69. 특정 유기체는 5가지 다른 유전자(영어 알파벳의 처음 5글자로 지정) 각각의 쌍을 가지고 있다. 각 유전자는 2가지 형태(소문자와 대문자로 지정)로 나타난다. 대문자는 우성 유전자로 가정되며, 이는 유기체가 유전자 쌍 $x X$를 가질 경우 겉으로는 $X$ 유전자의 모습을 가질 것이라는 의미이다. 예를 들어, $X$가 갈색 눈을, $x$가 파란 눈을 나타낸다면, 유전자 쌍 $X X$ 또는 $x X$를 가진 개체는 갈색 눈을 가질 것이고, 유전자 쌍 $x x$를 가진 개체는 파란 눈을 가질 것이다. 유기체의 특징적인 외형을 **표현형(phenotype)**이라고 하고, 유전적 구성을 **유전자형(genotype)**이라고 한다. (따라서 각각 유전자형 $a A, b B, c c, d D, e e$와 $A A, B B, c c, D D, ee$를 가진 두 유기체는 다른 유전자형을 가지지만 같은 표현형을 가질 것이다.) 두 유기체 간의 교배에서, 각 유기체는 각 유형의 유전자 쌍 중 하나를 무작위로 기여한다. 유기체의 5가지 기여(5가지 유형 각각에 대해 하나씩)는 독립적이며, 또한 짝의 기여와도 독립적이라고 가정한다. 유전자형 $a A, b B, c C, d D, e E$와 $a a, b B, c c, D d, e e$를 가진 유기체 간의 교배에서 자손이 (i) 표현형적으로 그리고 (ii) 유전자형적으로 다음을 닮을 확률은 얼마인가? (a) 첫 번째 부모 (b) 두 번째 부모 (c) 어느 한 부모 (d) 어느 부모도 닮지 않을 확률 3.70. 여왕이 혈우병 유전자를 가지고 있을 확률은 50-50이다. 그녀가 보인자라면, 각 왕자는 50-50 확률로 혈우병에 걸릴 수 있다. 여왕이 질병 없는 세 명의 왕자를 낳았다면, 여왕이 보인자일 확률은 얼마인가? 넷째 왕자가 있다면, 그가 혈우병에 걸릴 확률은 얼마인가? 3.71. 1982년 9월 30일 아침, 내셔널 리그 서부 지구의 세 선두 야구팀의 승패 기록은 다음과 같았다. | 팀 | 승 | 패 | | :--- | :---: | :---: | | 애틀랜타 브레이브스 | 87 | 72 | | 샌프란시스코 자이언츠 | 86 | 73 | | 로스앤젤레스 다저스 | 86 | 73 | 각 팀은 3경기가 남아 있었다. 자이언츠의 3경기는 모두 다저스와의 경기였고, 브레이브스의 남은 3경기는 샌디에이고 파드레스와의 경기였다. 남은 모든 경기의 결과는 독립적이며, 각 경기는 어느 참가자든 이길 확률이 같다고 가정하자. 각 팀이 지구 우승을 차지할 확률은 얼마인가? 두 팀이 1위로 동률을 이루면 플레이오프 경기를 치르며, 각 팀은 이길 확률이 같다. 3.72. 7명의 위원으로 구성된 시의회에는 3명으로 구성된 운영 위원회가 있다. 새로운 법안 아이디어는 먼저 운영 위원회로 가서, 3명의 위원 중 적어도 2명이 법안을 승인하면 전체 의회로 넘어간다. 전체 의회에 제출되면 법안은 통과를 위해 과반수 투표(적어도 4표)를 필요로 한다. 새로운 법안을 고려하고, 각 시의회 위원이 독립적으로 확률 $p$로 법안을 승인한다고 가정하자. 특정 운영 위원회 위원의 투표가 결정적일 확률은 얼마인가? 즉, 그 사람의 투표가 뒤집히면 법안의 최종 운명도 뒤집힐 확률은 얼마인가? 운영 위원회에 속하지 않은 특정 시의회 위원에 대한 해당 확률은 얼마인가? 3.73. 부부에게 태어나는 각 자녀는 가족 내 다른 자녀의 성별 분포와 독립적으로 남아 또는 여아일 확률이 같다고 가정하자. 5명의 자녀를 둔 부부에 대해 다음 사건들의 확률을 계산하시오. (a) 모든 자녀가 같은 성별일 확률 (b) 맏이 3명은 남아이고 나머지는 여아일 확률 (c) 정확히 3명이 남아일 확률 (d) 가장 나이 많은 2명이 여아일 확률 (e) 적어도 1명의 여아가 있을 확률 3.74. $A$와 $B$는 번갈아 가며 주사위 한 쌍을 굴리는데, $A$가 합계 9를 굴리거나 $B$가 합계 6을 굴릴 때 멈춘다. $A$가 먼저 굴린다고 가정할 때, 마지막 굴림이 $A$에 의해 이루어질 확률을 구하시오. 3.75. 특정 마을에서는 맏아들(또는 두 아들 가족의 경우 나이 많은 아들)과 그의 아내가 부모가 나이가 들었을 때 돌보는 것이 전통이다. 그러나 최근 몇 년 동안 이 마을의 여성들은 그 책임을 원하지 않아 맏아들과 결혼하는 것을 좋게 보지 않았다. (a) 마을의 모든 가족이 두 자녀를 가지고 있다면, 모든 아들 중 맏아들의 비율은 얼마인가? (b) 마을의 모든 가족이 세 자녀를 가지고 있다면, 모든 아들 중 맏아들의 비율은 얼마인가? 각 자녀는 독립적으로 남아 또는 여아일 확률이 같다고 가정하시오. 3.76. $E$와 $F$가 한 실험의 상호 배타적인 사건이라고 가정하자. 이 실험의 독립적인 시행이 수행될 때, $E$가 $F$보다 먼저 발생할 확률이 $P(E) /[P(E)+P(F)]$임을 보이시오. 3.77. 끝없는 독립 시행의 연속을 고려하시오. 각 시행은 결과 1, 2, 또는 3 중 하나를 가져올 확률이 같다고 가정하자. 결과 3이 세 결과 중 마지막으로 발생했다고 가정할 때, 다음 조건부 확률을 구하시오. (a) 첫 번째 시행 결과가 1일 확률 (b) 처음 두 시행 모두 결과가 1일 확률 3.78. $A$와 $B$는 일련의 게임을 한다. 각 게임은 $A$가 확률 $p$로, $B$가 확률 $1-p$로 독립적으로 승리한다. 한 플레이어의 총 승리 횟수가 다른 플레이어보다 두 번 더 많아질 때까지 멈춘다. 총 승리 횟수가 더 많은 플레이어가 시리즈의 승자로 선언된다. (a) 총 4경기가 치러질 확률을 구하시오. (b) $A$가 시리즈의 승자가 될 확률을 구하시오. 3.79. 한 쌍의 공정한 주사위를 연속적으로 굴릴 때, 짝수 6개가 나오기 전에 7이 두 번 나올 확률은 얼마인가? 3.80. 특정 대회에서 선수들은 실력이 동등하며, 두 참가자 중 특정 한 명이 승자가 될 확률은 $\frac{1}{2}$이다. $2^{n}$명의 선수 그룹에서 선수들은 무작위로 짝을 이룬다. $2^{n-1}$명의 승자는 다시 무작위로 짝을 이루고, 이런 식으로 한 명의 최종 승자가 남을 때까지 계속된다. 특정 두 참가자 $A$와 $B$를 고려하고, 사건 $A_{i}, i \leq n, E$를 다음과 같이 정의하시오.\begin{aligned} A_{i}: & A \text {는 정확히 } i \text{번의 경기에 출전한다.} \ E: & A \text{와 } B \text{는 서로 경기를 하지 않는다.} \end{aligned}
(a) $P\left(A_{i}\right), i=1, \ldots, n$을 구하시오. (b) $P(E)$를 구하시오. (c) $P_{n}=P(E)$라고 하자. 다음을 보이시오.P_{n}=\frac{1}{2^{n}-1}+\frac{2^{n}-2}{2^{n}-1}\left(\frac{1}{2}\right)^{2} P_{n-1}
그리고 이 공식을 사용하여 (b) 부분에서 얻은 답을 확인하시오. 힌트: 사건 $A_{i}, i=1, \ldots, n$ 중 어떤 것이 발생하는지에 따라 조건화하여 $P(E)$를 구하시오. 답을 단순화할 때 다음 대수적 항등식을 사용하시오.\sum_{i=1}^{n-1} i x^{i-1}=\frac{1-n x^{n-1}+(n-1) x^{n}}{(1-x)^{2}}
이 문제를 해결하는 또 다른 접근 방식은 총 $2^{n}-1$개의 게임이 진행된다는 점에 주목하는 것이다. (d) $2^{n}-1$개의 게임이 진행되는 이유를 설명하시오. 이 게임들에 번호를 매기고, $B_{i}$를 $A$와 $B$가 $i$번째 게임에서 서로 경기를 할 사건이라고 하자. 여기서 $i=1, \ldots, 2^{n}-1$이다. (e) $P\left(B_{i}\right)$는 얼마인가? (f) (e) 부분을 사용하여 $P(E)$를 구하시오. 3.81. 한 투자자가 현재 가치가 25인 주식을 소유하고 있다. 그녀는 주식이 10으로 떨어지거나 40으로 오르면 주식을 팔기로 결정했다. 각 가격 변동이 확률 .55로 1포인트 상승하거나 확률 .45로 1포인트 하락하며, 연속적인 변동이 독립적이라면, 투자자가 승자로 은퇴할 확률은 얼마인가? 3.82. $A$와 $B$는 동전을 던진다. $A$가 먼저 던지기 시작하여 뒷면이 나올 때까지 계속 던지고, 그 시점에서 $B$가 던지기 시작하여 뒷면이 나올 때까지 계속 던진다. 그런 다음 $A$가 다시 던지고, 이런 식으로 계속된다. $A$가 던질 때 동전이 앞면이 나올 확률을 $P_{1}$이라고 하고, $B$가 던질 때 앞면이 나올 확률을 $P_{2}$라고 하자. 게임의 승자는 다음을 먼저 얻는 사람이다. (a) 연속으로 2개의 앞면 (b) 총 2개의 앞면 (c) 연속으로 3개의 앞면 (d) 총 3개의 앞면 각 경우에 $A$가 이길 확률을 구하시오. 3.83. 주사위 $A$는 빨간 면 4개와 흰 면 2개를 가지고 있고, 주사위 $B$는 빨간 면 2개와 흰 면 4개를 가지고 있다. 공정한 동전을 한 번 던진다. 앞면이 나오면 주사위 $A$로 게임을 계속하고, 뒷면이 나오면 주사위 $B$를 사용한다. (a) 어떤 던지기에서든 빨간색이 나올 확률이 $\frac{1}{2}$임을 보이시오. (b) 처음 두 번의 던지기에서 빨간색이 나왔을 때, 세 번째 던지기에서 빨간색이 나올 확률은 얼마인가? (c) 처음 두 번의 던지기에서 빨간색이 나왔을 때, 사용되고 있는 주사위가 $A$일 확률은 얼마인가? 3.84. 항아리에는 12개의 공이 들어 있는데, 그 중 4개는 흰 공이다. 세 명의 플레이어 $A, B, C$가 항아리에서 차례로 공을 뽑는다. $A$가 먼저, 그 다음 $B$, 그 다음 $C$, 그 다음 $A$ 등으로 계속된다. 승자는 흰 공을 먼저 뽑는 사람이다. 각 플레이어의 승리 확률을 구하시오. (a) 각 공이 뽑힌 후 다시 넣어지는 경우 (b) 뽑힌 공이 다시 넣어지지 않는 경우 3.85. 각 3명의 플레이어가 자신의 항아리에서 선택하는 경우 문제 3.84를 반복하시오. 즉, 각각 4개의 흰 공이 들어 있는 12개의 공이 있는 3개의 다른 항아리가 있다고 가정하자. 3.86. $S=\{1,2, \ldots, n\}$이라고 하고, $A$와 $B$가 독립적으로 $S$의 $2^{n}$개 부분집합(공집합과 $S$ 자체 포함) 중 어느 하나일 확률이 같다고 가정하자. (a) 다음을 보이시오.P{A \subset B}=\left(\frac{3}{4}\right)^{n}
힌트: $N(B)$를 $B$의 원소 수라고 하자. 다음을 사용하시오.P{A \subset B}=\sum_{i=0}^{n} P{A \subset B \mid N(B)=i} P{N(B)=i}
$P\{A B=\varnothing\}=\left(\frac{3}{4}\right)^{n}$임을 보이시오. 3.87. 예제 2a를 고려하되, 이제 열쇠가 특정 주머니에 있을 때 그 주머니를 찾아도 열쇠를 찾지 못할 확률이 10%라고 가정하자. $R$과 $L$을 각각 열쇠가 재킷의 오른쪽 주머니에 있는 사건과 왼쪽 주머니에 있는 사건이라고 하자. 또한, $S_{R}$을 재킷의 오른쪽 주머니를 찾아 열쇠를 찾는 데 성공할 사건이라고 하고, $U_{L}$을 재킷의 왼쪽 주머니를 찾는 데 실패하여 열쇠를 찾지 못할 사건이라고 하자. 왼쪽 주머니를 찾았는데 열쇠를 찾지 못했을 때, 오른쪽 주머니를 찾으면 열쇠를 찾을 조건부 확률 $P\left(S_{R} \mid U_{L}\right)$을 다음을 사용하여 구하시오. (a) 항등식 사용P\left(S_{R} \mid U_{L}\right)=\frac{P\left(S_{R} U_{L}\right)}{P\left(U_{L}\right)}
$P\left(S_{R} U_{L}\right)$을 열쇠가 오른쪽 주머니에 있는지 여부에 따라 조건화하여 결정하고, $P\left(U_{L}\right)$을 열쇠가 왼쪽 주머니에 있는지 여부에 따라 조건화하여 결정하시오. (b) 항등식 사용\begin{aligned} P\left(S_{R} \mid U_{L}\right)= & P\left(S_{R} \mid R U_{L}\right) P\left(R \mid U_{L}\right) \ & +P\left(S_{R} \mid R^{c} U_{L}\right) P\left(R^{c} \mid U_{L}\right) \end{aligned}
3.88. 예제 5e에서, 처음 $n$번의 시행이 모두 앞면이 나왔을 때 $i$번째 동전이 선택되었을 조건부 확률은 얼마인가? 3.89. 라플라스의 계승 규칙(예제 5e)에서 연속적인 던지기의 결과는 독립적인가? 설명하시오. 3.90. 3명의 판사 패널에 의해 재판을 받는 사람은 적어도 2명의 판사가 유죄 투표를 하면 유죄로 선고된다. 피고인이 실제로 유죄일 때 각 판사는 독립적으로 확률 .7로 유죄 투표를 하고, 피고인이 실제로 무죄일 때는 이 확률이 .2로 떨어진다고 가정하자. 피고인의 70%가 유죄일 때, 다음 조건부 확률을 계산하시오. (a) 판사 1과 2가 유죄 투표를 했을 때 판사 3이 유죄 투표를 할 확률 (b) 판사 1과 2가 유죄 1표와 무죄 1표를 던졌을 때 판사 3이 유죄 투표를 할 확률 (c) 판사 1과 2가 모두 무죄 투표를 했을 때 판사 3이 유죄 투표를 할 확률 $E_{i}, i=1,2,3$를 판사 $i$가 유죄 투표를 하는 사건이라고 하자. 이 사건들은 독립적인가? 조건부 독립적인가? 설명하시오. 3.91. $n$번의 독립 시행이 수행된다고 가정하자. 각 시행은 각각 확률 $p_{0}, p_{1}, p_{2}$로 결과 0, 1, 또는 2 중 하나를 가져온다. 여기서 $\sum_{i=0}^{2} p_{i}=1$이다. 결과 1과 2가 모두 적어도 한 번 발생할 확률을 구하시오. ## Theoretical Exercises 3.1. $P(A)>0$일 때 다음을 보이시오:P(A B \mid A) \geq P(A B \mid A \cup B)
3.2. $A \subset B$라고 하자. 다음 확률을 가능한 한 간단하게 표현하시오:P(A \mid B), \quad P\left(A \mid B^{c}\right), \quad P(B \mid A), \quad P\left(B \mid A^{c}\right)
3.3. $m$개의 가족으로 구성된 학교 공동체를 생각해보자. 이 중 $n_i$개의 가족은 $i$명의 자녀를 가지고 있으며, $i=1, \ldots, k, \sum_{i=1}^{k} n_{i}=m$이다. 다음 두 가지 방법으로 자녀를 선택하는 경우를 고려해보자: 1. $m$개의 가족 중 하나를 무작위로 선택한 다음, 그 가족에서 자녀 한 명을 무작위로 선택한다. 2. $\sum_{i=1}^{k} i n_{i}$명의 자녀 중 한 명을 무작위로 선택한다. 방법 1이 방법 2보다 첫째 자녀를 선택할 가능성이 더 높다는 것을 보이시오. 힌트: 이 문제를 해결하려면 다음을 보여야 한다:\sum_{i=1}^{k} i n_{i} \sum_{j=1}^{k} \frac{n_{j}}{j} \geq \sum_{i=1}^{k} n_{i} \sum_{j=1}^{k} n_{j}
이를 위해 합을 곱하고, 모든 쌍 $i, j$에 대해 $n_i n_j$ 항의 계수가 오른쪽 식보다 왼쪽 식에서 더 크다는 것을 보이시오. 3.4. 공이 $n$개의 상자 중 하나에 들어 있으며, $i$번째 상자에 있을 확률은 $P_i$이다. 공이 $i$번째 상자에 있을 때, 그 상자를 수색하면 확률 $\alpha_i$로 공을 발견할 수 있다. $i$번째 상자를 수색했지만 공을 발견하지 못했을 때, 공이 $j$번째 상자에 있을 조건부 확률이 다음과 같음을 보이시오:\begin{gathered} \frac{P_{j}}{1-\alpha_{i} P_{i}} \quad \text { if } j \neq i \ \frac{\left(1-\alpha_{i}\right) P_{i}}{1-\alpha_{i} P_{i}} \quad \text { if } j = i \end{gathered}
3.5. (a) $E$와 $F$가 상호 배타적(mutually exclusive)이라면 다음을 증명하시오:P(E \mid E \cup F)=\frac{P(E)}{P(E)+P(F)}
(b) $E_i, i \geq 1$이 상호 배타적이라면 다음을 증명하시오:P\left(E j \mid \cup_{i=1}^{\infty} E_{i}\right)=\frac{P\left(E_{j}\right)}{\sum_{i=1}^{\infty} P\left(E_{i}\right)}
3.6. $E_1, E_2, \ldots, E_n$이 독립 사건(independent events)이라면 다음을 증명하시오:P\left(E_{1} \cup E_{2} \cup \cdots \cup E_{n}\right)=1-\prod_{i=1}^{n}\left[1-P\left(E_{i}\right)\right]
3.7. (a) 항아리에 $n$개의 흰 공과 $m$개의 검은 공이 들어 있다. 같은 색의 공만 남을 때까지 공을 한 번에 하나씩 꺼낸다. 확률 $n/(n+m)$으로 모든 공이 흰색임을 보이시오. 힌트: 모든 공이 제거될 때까지 실험이 계속된다고 상상하고, 마지막으로 꺼낸 공을 고려해보시오. (b) 연못에 3가지 종류의 물고기(빨간색, 파란색, 녹색)가 있다. 빨간색 물고기는 $r$마리, 파란색 물고기는 $b$마리, 녹색 물고기는 $g$마리가 있다. 물고기가 연못에서 무작위 순서로 제거된다고 가정하자. (즉, 각 선택은 남아있는 물고기 중 어느 것이든 동일한 확률로 선택된다.) 빨간색 물고기가 연못에서 가장 먼저 멸종하는 종일 확률은 얼마인가? 힌트: $P\{R\}=P\{R B G\}+P\{R G B\}$로 쓰고, 제거될 마지막 종에 먼저 조건화하여 오른쪽 확률을 계산하시오. 3.8. $A, B, C$를 한 쌍의 주사위를 굴리는 실험과 관련된 사건이라고 하자. (a) 만약P(A \mid C)>P(B \mid C) \quad \text { 이고 } \quad P\left(A \mid C^{c}\right)>P\left(B \mid C^{c}\right)
이면 $P(A)>P(B)$임을 증명하거나, 이 관계가 성립하지 않는 사건 $A, B, C$를 정의하여 반례를 제시하시오. (b) 만약P(A \mid C)>P\left(A \mid C^{c}\right) \quad \text { 이고 } \quad P(B \mid C)>P\left(B \mid C^{c}\right)
이면 $P(A B \mid C)>P\left(A B \mid C^{c}\right)$임을 증명하거나, 이 관계가 성립하지 않는 사건 $A, B, C$를 정의하여 반례를 제시하시오. 힌트: $C$를 한 쌍의 주사위 합이 10인 사건으로, $A$를 첫 번째 주사위가 6이 나오는 사건으로, $B$를 두 번째 주사위가 6이 나오는 사건으로 두시오. 3.9. 공정한 동전을 두 번 독립적으로 던지는 경우를 생각해보자. $A$를 첫 번째 던지기에서 앞면이 나오는 사건, $B$를 두 번째 던지기에서 앞면이 나오는 사건, $C$를 두 번 모두 같은 면이 나오는 사건이라고 하자. 사건 $A, B, C$가 **쌍별 독립(pairwise independent)**임을 보이시오. 즉, $A$와 $B$는 독립이고, $A$와 $C$는 독립이며, $B$와 $C$는 독립이지만, 이들이 **독립은 아님**을 보이시오. 3.10. 정기 검진에 참여하는 45세 여성의 2%가 유방암을 앓고 있다. 유방암 환자의 90%는 유방 촬영술에서 양성 판정을 받는다. 유방암이 없는 여성의 8%도 유방 촬영술에서 양성 판정을 받는다. 한 여성이 유방 촬영술에서 양성 판정을 받았을 때, 그녀가 유방암을 앓고 있을 확률은 얼마인가? 3.11. $n$번의 독립적인 동전 던지기에서 동전이 앞면이 나올 확률은 $p$이다. 적어도 한 번의 앞면이 나올 확률이 $\frac{1}{2}$ 이상이 되려면 $n$은 얼마나 커야 하는가? 3.12. $0 \leq a_i \leq 1, i=1,2, \ldots$일 때 다음을 보이시오:\sum_{i=1}^{\infty}\left[a_{i} \prod_{j=1}^{i-1}\left(1-a_{j}\right)\right]+\prod_{i=1}^{\infty}\left(1-a_{i}\right)=1
힌트: 무한히 많은 동전을 던진다고 가정해보자. $a_i$를 $i$번째 동전이 앞면이 나올 확률이라고 하고, 첫 번째 앞면이 언제 나오는지 고려해보시오. 3.13. 동전을 한 번 던져 앞면이 나올 확률은 $p$이다. $A$가 먼저 동전을 던지기 시작하여 뒷면이 나올 때까지 계속 던지고, 뒷면이 나오면 $B$가 던지기 시작한다. $B$는 뒷면이 나올 때까지 계속 던지고, 뒷면이 나오면 $A$가 다시 던지는 식으로 계속된다. $P_{n, m}$을 $B$가 $m$개의 앞면을 모으기 전에 $A$가 총 $n$개의 앞면을 모을 확률이라고 하자. 다음을 보이시오:P_{n, m}=p P_{n-1, m}+(1-p)\left(1-P_{m, n}\right)
*3.14. 무한히 부유한 상대와 도박을 한다고 가정하자. 각 단계에서 당신은 확률 $p$로 1단위를 얻거나 확률 $1-p$로 1단위를 잃는다. 당신이 결국 파산할 확률이 다음과 같음을 보이시오:\begin{array}{cl} 1 & \text { if } p \leq \frac{1}{2} \ (q / p)^{i} & \text { if } p>\frac{1}{2} \end{array}
여기서 $q=1-p$이고 $i$는 당신의 초기 자산이다. 3.15. 확률 $p$로 성공하는 독립 시행이 총 $r$번의 성공을 얻을 때까지 연속적으로 수행된다. 정확히 $n$번의 시행이 필요할 확률이 다음과 같음을 보이시오:\binom{n-1}{r-1} p^{r}(1-p)^{n-r}
이 결과를 사용하여 점수 문제(예제 4j)를 해결하시오. 힌트: $r$번의 성공을 얻는 데 $n$번의 시행이 필요하려면 처음 $n-1$번의 시행에서 몇 번의 성공이 발생해야 하는가? 3.16. 확률 $p$로 성공하고 확률 $1-p$로 실패하는 독립 시행을 **베르누이 시행(Bernoulli trials)**이라고 한다. $P_n$을 $n$번의 베르누이 시행에서 짝수 번의 성공(0은 짝수로 간주)이 발생할 확률이라고 하자. 다음을 보이시오:P_{n}=p\left(1-P_{n-1}\right)+(1-p) P_{n-1} \quad n \geq 1
P_{n}=\frac{1+(1-2 p)^{n}}{2}
3.17. $n$번의 독립 시행이 수행되며, $i$번째 시행이 성공할 확률은 $1/(2i+1)$이라고 가정하자. $P_n$을 총 성공 횟수가 홀수일 확률이라고 하자. (a) $n=1,2,3,4,5$에 대해 $P_n$을 구하시오. (b) $P_n$에 대한 일반적인 공식을 추측하시오. (c) $P_{n-1}$을 사용하여 $P_n$에 대한 공식을 도출하시오. (d) (b)에서 추측한 공식이 (c)의 재귀 공식을 만족하는지 확인하시오. 재귀 공식은 유일한 해를 가지므로, 이는 당신의 추측이 옳다는 것을 증명한다. 3.18. $Q_n$을 공정한 동전을 $n$번 던졌을 때 3번 연속 앞면이 나오지 않을 확률이라고 하자. 다음을 보이시오:\begin{aligned} & Q_{n}=\frac{1}{2} Q_{n-1}+\frac{1}{4} Q_{n-2}+\frac{1}{8} Q_{n-3} \ & Q_{0}=Q_{1}=Q_{2}=1 \end{aligned}
$Q_8$을 구하시오. 힌트: 첫 번째 뒷면에 조건화하시오. 3.19. 도박사의 파산 문제(gambler's ruin problem)를 고려하되, $A$와 $B$가 $n$게임 이상 플레이하지 않기로 합의했다고 가정하자. $P_{n, i}$를 $A$가 $i$를 가지고 시작하고 $B$가 $N-i$를 가지고 시작할 때 $A$가 모든 돈을 얻을 확률이라고 하자. $P_{n, i}$를 $P_{n-1, i+1}$과 $P_{n-1, i-1}$로 표현하는 방정식을 도출하고, $N=5$일 때 $P_{7,3}$을 계산하시오. 3.20. 각각 흰 공과 검은 공을 모두 포함하는 두 개의 항아리를 생각해보자. 첫 번째 항아리와 두 번째 항아리에서 흰 공을 뽑을 확률은 각각 $p$와 $p'$이다. 공은 다음과 같은 방법으로 교체하여 순차적으로 선택된다: 확률 $\alpha$로 처음에는 첫 번째 항아리에서 공을 선택하고, 확률 $1-\alpha$로 두 번째 항아리에서 공을 선택한다. 이후의 선택은 흰 공이 뽑히면 (그리고 교체되면) 다음 공은 같은 항아리에서 뽑히고, 검은 공이 뽑히면 다음 공은 다른 항아리에서 뽑히는 규칙에 따라 이루어진다. $\alpha_n$을 $n$번째 공이 첫 번째 항아리에서 선택될 확률이라고 하자. 다음을 보이시오:\alpha_{n+1}=\alpha_{n}\left(p+p^{\prime}-1\right)+1-p^{\prime} \quad n \geq 1
\begin{aligned} \alpha_{n}= & \frac{1-p^{\prime}}{2-p-p^{\prime}}+\left(\alpha-\frac{1-p^{\prime}}{2-p-p^{\prime}}\right) \ & \times\left(p+p^{\prime}-1\right)^{n-1} \end{aligned}
$P_n$을 $n$번째 선택된 공이 흰색일 확률이라고 하자. $P_n$을 구하시오. 또한 $\lim _{n \rightarrow \infty} \alpha_{n}$과 $\lim _{n \rightarrow \infty} P_{n}$을 계산하시오. 3.21. **투표 문제(The Ballot Problem)**. 선거에서 후보 $A$는 $n$표를 받고 후보 $B$는 $m$표를 받는데, $n>m$이다. $(n+m)!/ n!m!$개의 모든 투표 순서가 동일하게 가능하다고 가정할 때, $P_{n, m}$을 투표 개표 과정에서 $A$가 항상 앞서 있을 확률이라고 하자. (a) $P_{2,1}, P_{3,1}, P_{3,2}, P_{4,1}, P_{4,2}, P_{4,3}$을 계산하시오. (b) $P_{n, 1}, P_{n, 2}$를 구하시오. (c) (a)와 (b)의 결과를 바탕으로 $P_{n, m}$의 값을 추측하시오. (d) 마지막 표를 누가 받았는지에 조건화하여 $P_{n, m}$을 $P_{n-1, m}$과 $P_{n, m-1}$로 표현하는 재귀 관계를 도출하시오. (e) (d)를 사용하여 (c)의 추측을 $n+m$에 대한 귀납법 증명으로 확인하시오. 3.22. 날씨 예측에 대한 단순화된 모델로, 내일 날씨(습하거나 건조하거나)가 오늘 날씨와 같을 확률이 $p$라고 가정하자. 1월 1일 날씨가 건조하다면, $n$일 후 날씨가 건조할 확률인 $P_n$이 다음을 만족함을 보이시오:\begin{aligned} & P_{n}=(2 p-1) P_{n-1}+(1-p) \quad n \geq 1 \ & P_{0}=1 \end{aligned}
P_{n}=\frac{1}{2}+\frac{1}{2}(2 p-1)^{n} \quad n \geq 0
3.23. 주머니에 $a$개의 흰 공과 $b$개의 검은 공이 들어 있다. 공은 다음 방법에 따라 주머니에서 선택된다: 1. 공을 무작위로 선택하여 버린다. 2. 두 번째 공을 선택한다. 만약 그 색깔이 이전 공과 다르면, 주머니에 다시 넣고 과정을 처음부터 반복한다. 만약 색깔이 같으면, 그 공을 버리고 2단계부터 다시 시작한다. 다시 말해, 색깔이 바뀔 때까지 공을 뽑아서 버리고, 색깔이 바뀌면 마지막 공은 항아리에 다시 넣고 과정이 새로 시작된다. $P_{a, b}$를 주머니에 남은 마지막 공이 흰색일 확률이라고 하자. 다음을 증명하시오:P_{a, b}=\frac{1}{2}
힌트: $k \equiv a+b$에 대한 귀납법을 사용하시오. *3.24. $n$명의 참가자가 참여하는 **라운드 로빈 토너먼트(round-robin tournament)**는 $\binom{n}{2}$쌍의 참가자 각각이 정확히 한 번씩 경기를 하며, 각 경기의 결과는 한 참가자가 이기고 다른 참가자가 지는 것이다. 고정된 정수 $k, k<n$에 대해, 토너먼트 결과가 모든 $k$명의 선수 집합에 대해 그 집합의 각 구성원을 이긴 선수가 존재할 수 있는지 여부가 관심사이다. 만약 다음이 성립한다면 그러한 결과가 가능함을 보이시오:\binom{n}{k}\left[1-\left(\frac{1}{2}\right)^{k}\right]^{n-k}<1
힌트: 게임 결과가 독립적이고 각 게임이 어느 참가자에 의해 이겨질 확률이 동일하다고 가정하자. $k$명의 참가자 집합 $\binom{n}{k}$개에 번호를 매기고, $B_i$를 어떤 참가자도 $i$번째 집합의 $k$명의 선수를 모두 이기지 못한 사건이라고 하자. 그런 다음 **부울 부등식(Boole's inequality)**을 사용하여 $P\left(\bigcup_{i} B_{i}\right)$의 상한을 구하시오. 3.25. 다음을 직접 증명하시오:P(E \mid F)=P(E \mid F G) P(G \mid F)+P\left(E \mid F G^{c}\right) P\left(G^{c} \mid F\right)
3.26. 방정식 (5.11)과 (5.12)의 동등성을 증명하시오. 3.27. 조건부 독립(conditional independence)의 정의를 2개 이상의 사건으로 확장하시오. 3.28. 증명하거나 반례를 제시하시오. $E_1$과 $E_2$가 독립이라면, $F$가 주어졌을 때 조건부 독립이다. 3.29. 라플라스의 계승 규칙(Laplace's rule of succession, 예제 5e)에서, 처음 $n$번의 던지기가 모두 앞면이 나왔다면, 다음 $m$번의 던지기도 모두 앞면이 나올 조건부 확률이 $(n+1) /(n+m+1)$임을 보이시오. 3.30. 라플라스의 계승 규칙(예제 5e)에서, 처음 $n$번의 던지기에서 $r$번의 앞면과 $n-r$번의 뒷면이 나왔다고 가정하자. $(n+1)$번째 던지기에서 앞면이 나올 확률이 $(r+1) /(n+2)$임을 보이시오. 이를 위해 다음 항등식을 증명하고 사용해야 한다:\int_{0}^{1} y^{n}(1-y)^{m} d y=\frac{n!m!}{(n+m+1)!}
힌트: 항등식을 증명하기 위해 $C(n, m)=\int_{0}^{1} y^{n}(1-y)^{m} d y$라고 하자. 부분 적분을 하면 다음을 얻는다:C(n, m)=\frac{m}{n+1} C(n+1, m-1)
$C(n, 0)=1 /(n+1)$에서 시작하여 $m$에 대한 귀납법으로 항등식을 증명하시오. 3.31. 수학적이지는 않지만 철학적인 사고를 가진 친구가 라플라스의 계승 규칙이 터무니없는 결론으로 이어질 수 있기 때문에 틀렸다고 주장한다고 가정하자. 그는 "예를 들어, 이 규칙은 10년 동안 살아온 10살 소년이 1년 더 살 확률이 $\frac{11}{12}$라고 말합니다. 반면에 80세 할아버지가 있다면, 라플라스의 규칙에 따르면 할아버지가 1년 더 살 확률은 $\frac{81}{82}$입니다. 하지만 이것은 터무니없습니다. 분명히 소년이 할아버지보다 1년 더 살 가능성이 높습니다."라고 말한다. 당신은 친구에게 어떻게 대답하겠는가? ## Self-Test Problems and Exercises 3.1. 브리지 게임에서 웨스트는 에이스가 없다. 그의 파트너가 (a) 에이스가 없을 확률은? (b) 2개 이상의 에이스를 가질 확률은? (c) 웨스트가 정확히 1개의 에이스를 가지고 있다면 확률은 어떻게 될까? 3.2. 새 자동차 배터리가 10,000마일 이상 작동할 확률은 .8이고, 20,000마일 이상 작동할 확률은 .4이며, 30,000마일 이상 작동할 확률은 .1이다. 새 자동차 배터리가 10,000마일 후에도 여전히 작동한다면, 다음 확률은 얼마인가? (a) 총 수명이 20,000마일을 초과할 확률은? (b) 추가 수명이 20,000마일을 초과할 확률은? 3.3. 10개의 흰 공과 10개의 검은 공, 총 20개의 공을 두 개의 항아리에 어떻게 넣어야 무작위로 항아리를 선택하고 그 항아리에서 무작위로 공을 뽑을 때 흰 공을 뽑을 확률을 최대화할 수 있을까? 3.4. 항아리 $A$에는 흰 공 2개와 검은 공 1개가 들어있고, 항아리 $B$에는 흰 공 1개와 검은 공 5개가 들어있다. 항아리 $A$에서 무작위로 공을 뽑아 항아리 $B$에 넣는다. 그런 다음 항아리 $B$에서 공을 뽑는다. 그 공이 흰색으로 판명되었다. 옮겨진 공이 흰색이었을 확률은 얼마인가? 3.5. 항아리에 $r$개의 빨간 공과 $w$개의 흰 공이 있으며, 이 공들은 한 번에 하나씩 무작위로 제거된다. $R_{i}$를 $i$번째 제거된 공이 빨간색인 사건이라고 하자. 다음을 구하라. (a) $P\left(R_{i}\right)$ (b) $P\left(R_{5} \mid R_{3}\right)$ (c) $P\left(R_{3} \mid R_{5}\right)$ 3.6. 항아리에 $b$개의 검은 공과 $r$개의 빨간 공이 들어있다. 공 하나를 무작위로 뽑지만, 다시 항아리에 넣을 때 같은 색깔의 공 $c$개를 추가로 넣는다. 이제 다른 공을 뽑는다고 가정하자. 두 번째 뽑은 공이 빨간색일 때, 첫 번째 공이 검은색이었을 확률이 $b /(b+r+c)$임을 보여라. 3.7. 친구가 52장의 일반 트럼프 카드 덱에서 두 장의 카드를 비복원 추출로 무작위로 뽑는다. 다음 각 상황에서 두 카드 모두 에이스일 조건부 확률을 결정하라. (a) 친구에게 카드 중 하나가 스페이드 에이스인지 물었고, 친구가 긍정적으로 답했다. (b) 친구에게 첫 번째 뽑은 카드가 에이스인지 물었고, 친구가 긍정적으로 답했다. (c) 친구에게 두 번째 뽑은 카드가 에이스인지 물었고, 친구가 긍정적으로 답했다. (d) 친구에게 뽑은 카드 중 하나라도 에이스인지 물었고, 친구가 긍정적으로 답했다. 3.8. 다음을 보여라.\frac{P(H \mid E)}{P(G \mid E)}=\frac{P(H)}{P(G)} \frac{P(E \mid H)}{P(E \mid G)}
새로운 증거가 관찰되기 전에 가설 $H$가 가설 $G$보다 참일 가능성이 세 배 더 높다고 가정하자. 새로운 증거가 $G$가 참일 때 $H$가 참일 때보다 두 배 더 가능성이 있다면, 증거가 관찰된 후 어떤 가설이 더 가능성이 높은가? 3.9. 당신이 휴가 중일 때 이웃에게 병든 식물에 물을 주도록 부탁했다. 물을 주지 않으면 0.8의 확률로 죽고, 물을 주면 0.15의 확률로 죽는다. 당신은 이웃이 식물에 물을 줄 것이라고 90% 확신한다. (a) 당신이 돌아왔을 때 식물이 살아있을 확률은 얼마인가? (b) 당신이 돌아왔을 때 식물이 죽어있다면, 이웃이 물 주는 것을 잊었을 확률은 얼마인가? 3.10. 8개의 빨간 공, 10개의 초록 공, 12개의 파란 공이 들어있는 항아리에서 6개의 공을 무작위로 뽑는다. (a) 적어도 하나의 빨간 공이 뽑힐 확률은 얼마인가? (b) 빨간 공이 하나도 뽑히지 않았을 때, 뽑힌 6개의 공 중에 정확히 2개의 초록 공이 있을 조건부 확률은 얼마인가? 3.11. C형 배터리는 0.7의 확률로 작동하고, D형 배터리는 0.4의 확률로 작동한다. C형 배터리 8개와 D형 배터리 6개로 구성된 통에서 배터리 하나를 무작위로 선택한다. (a) 배터리가 작동할 확률은 얼마인가? (b) 배터리가 작동하지 않을 때, 그것이 C형 배터리였을 조건부 확률은 얼마인가? 3.12. 마리아는 여행에 두 권의 책을 가져갈 것이다. 그녀가 책 1을 좋아할 확률은 .6이고, 책 2를 좋아할 확률은 .5이며, 두 책 모두를 좋아할 확률은 .4라고 가정하자. 그녀가 책 1을 좋아하지 않았을 때 책 2를 좋아할 조건부 확률을 구하라. 3.13. 처음에는 빨간 공 20개와 파란 공 10개가 들어있는 항아리에서 공을 무작위로 제거한다. (a) 모든 파란 공이 제거되기 전에 모든 빨간 공이 제거될 확률은 얼마인가? 이제 항아리에 처음에는 빨간 공 20개, 파란 공 10개, 초록 공 8개가 들어있다고 가정하자. (b) 이제 모든 파란 공이 제거되기 전에 모든 빨간 공이 제거될 확률은 얼마인가? (c) 파란색, 빨간색, 초록색 순서로 공이 고갈될 확률은 얼마인가? (d) 파란 공 그룹이 세 그룹 중 가장 먼저 제거될 확률은 얼마인가? 3.14. 앞면이 나올 확률이 .8인 동전을 던진다. $A$는 결과(앞면 또는 뒷면)를 관찰하고 $B$에게 알리러 달려간다. 그러나 $A$는 $B$에게 도착할 때까지 0.4의 확률로 결과를 잊어버릴 것이다. $A$가 잊어버렸다면, $B$에게 이를 인정하기보다는 동전이 앞면으로 나왔다고 말하거나 뒷면으로 나왔다고 말할 가능성이 똑같이 높다. (만약 기억한다면 $B$에게 정확한 결과를 말한다.) (a) $B$가 동전이 앞면으로 나왔다고 들을 확률은 얼마인가? (b) $B$가 정확한 결과를 들을 확률은 얼마인가? (c) $B$가 동전이 앞면으로 나왔다고 들었을 때, 실제로 앞면으로 나왔을 확률은 얼마인가? 3.15. 특정 쥐 종에서 검은색이 갈색보다 우성이다. 두 검은색 부모를 가진 검은색 쥐가 갈색 형제를 가지고 있다고 가정하자. (a) 이 쥐가 순수 검은색 쥐(하나의 검은색 유전자와 하나의 갈색 유전자를 가진 잡종이 아닌)일 확률은 얼마인가? (b) 검은색 쥐가 갈색 쥐와 교배했을 때, 5마리의 새끼 모두 검은색이라고 가정하자. 이제 이 쥐가 순수 검은색 쥐일 확률은 얼마인가? 3.16. (a) 문제 3.66b에서 릴레이 1이 닫히는지 여부에 따라 조건화하여 $A$에서 $B$로 전류가 흐를 확률을 구하라. (b) $A$에서 $B$로 전류가 흐를 때 릴레이 3이 닫혀 있을 조건부 확률을 구하라. 3.17. 문제 3.67에 설명된 $k$-out-of-$n$ 시스템에 대해 각 구성 요소가 독립적으로 $\frac{1}{2}$의 확률로 작동한다고 가정하자. 시스템이 작동할 때 구성 요소 1이 작동할 조건부 확률을 구하라. (a) $k=1, n=2$; (b) $k=2, n=3$. 3.18. 존스 씨는 룰렛에서 이기는 도박 시스템을 고안했다. 그는 빨간색에 베팅하며, 룰렛의 이전 10번의 스핀이 모두 검은색 숫자에 멈췄을 때만 베팅한다. 그는 11번 연속 스핀이 검은색으로 나올 확률이 매우 작기 때문에 이길 확률이 상당히 크다고 생각한다. 이 시스템에 대해 어떻게 생각하는가? 3.19. 세 명의 플레이어가 동시에 동전을 던진다. $A(B)[C]$가 던진 동전은 각각 $P_{1}\left(P_{2}\right)\left[P_{3}\right]$의 확률로 앞면이 나온다. 한 사람이 다른 두 사람과 다른 결과를 얻으면 그 사람이 **odd man out**이 된다. **odd man out**이 없으면 플레이어들은 다시 던지고 **odd man out**이 나올 때까지 계속한다. $A$가 **odd man**이 될 확률은 얼마인가? 3.20. 시행의 가능한 결과가 $n$개이고, 결과 $i$가 확률 $p_{i}$로 발생한다고 가정하자. 여기서 $i= 1, \ldots, n, \sum_{i=1}^{n} p_{i}=1$이다. 두 번의 독립적인 시행이 관찰될 때, 두 번째 시행의 결과가 첫 번째 시행의 결과보다 클 확률은 얼마인가? 3.21. $A$가 $n+1$개의 공정한 동전을 던지고 $B$가 $n$개의 공정한 동전을 던질 때, $A$가 $B$보다 더 많은 앞면을 얻을 확률이 $\frac{1}{2}$임을 보여라. 힌트: 각 플레이어가 $n$개의 동전을 던진 후 누가 더 많은 앞면을 가졌는지에 따라 조건화하라. (세 가지 가능성이 있다.) 3.22. 다음 진술에 대해 증명하거나 반례를 제시하라. (a) $E$가 $F$와 독립이고 $E$가 $G$와 독립이면, $E$는 $F \cup G$와 독립이다. (b) $E$가 $F$와 독립이고, $E$가 $G$와 독립이며, $F G=\varnothing$이면, $E$는 $F \cup G$와 독립이다. (c) $E$가 $F$와 독립이고, $F$가 $G$와 독립이며, $E$가 $F G$와 독립이면, $G$는 $E F$와 독립이다. 3.23. $A$와 $B$를 양의 확률을 갖는 사건이라고 하자. 다음 각 진술이 (i) 반드시 참인지, (ii) 반드시 거짓인지, 또는 (iii) 가능성이 있는지 명시하라. (a) $A$와 $B$가 상호 배타적이면, 그들은 독립이다. (b) $A$와 $B$가 독립이면, 그들은 상호 배타적이다. (c) $P(A)=P(B)=.6$이고, $A$와 $B$는 상호 배타적이다. (d) $P(A)=P(B)=.6$이고, $A$와 $B$는 독립이다. 3.24. 다음을 발생 가능성이 높은 순서부터 낮은 순서로 나열하라. 1. 공정한 동전이 앞면으로 나온다. 2. 각각 성공 확률이 .8인 세 번의 독립적인 시행이 모두 성공한다. 3. 각각 성공 확률이 .9인 일곱 번의 독립적인 시행이 모두 성공한다. 3.25. 두 지역 공장 $A$와 $B$는 라디오를 생산한다. 공장 $A$에서 생산된 각 라디오는 0.05의 확률로 불량이며, 공장 $B$에서 생산된 각 라디오는 0.01의 확률로 불량이다. 당신이 같은 공장에서 생산된 두 대의 라디오를 구매했다고 가정하자. 이 공장은 공장 $A$ 또는 공장 $B$일 가능성이 똑같이 높다. 당신이 확인한 첫 번째 라디오가 불량이라면, 다른 라디오도 불량일 조건부 확률은 얼마인가? 3.26. $P(A \mid B)=1$이면 $P\left(B^{c} \mid A^{c}\right)=1$임을 보여라. 3.27. 항아리에는 처음에는 빨간 공 1개와 파란 공 1개가 들어있다. 각 단계에서 공 하나를 무작위로 뽑아 같은 색깔의 다른 공 두 개로 교체한다. (예를 들어, 빨간 공이 처음 선택되면 다음 선택이 발생할 때 항아리에는 빨간 공 2개와 파란 공 1개가 있게 된다.) $n$단계가 완료된 후 항아리에 정확히 $i$개의 빨간 공이 있을 확률이 $\frac{1}{n+1}, 1 \leq i \leq n+1$임을 수학적 귀납법으로 보여라. 3.28. 2개의 에이스를 포함한 총 $2n$장의 카드를 두 명의 플레이어에게 무작위로 나누어주고, 각 플레이어는 $n$장의 카드를 받는다. 각 플레이어는 순서대로 에이스를 받았는지 여부를 선언한다. 첫 번째 플레이어가 긍정적으로 선언했을 때, 두 번째 플레이어가 에이스를 가지고 있지 않을 조건부 확률은 얼마인가? (a) $n=2$일 때? (b) $n=10$일 때? (c) $n=100$일 때? $n$이 무한대로 갈 때 확률은 어디로 수렴하는가? 그 이유는 무엇인가? 3.29. $n$가지의 서로 다른 유형의 쿠폰이 있으며, 수집된 각 쿠폰은 이전에 수집된 유형과 독립적으로 확률 $p_{i}$로 유형 $i$에 해당한다. 여기서 $\sum_{i=1}^{n} p_{i}=1$이다. (a) $n$개의 쿠폰이 수집될 때, 각 유형의 쿠폰이 하나씩 얻어질 확률은 얼마인가? (b) 이제 $p_{1}=p_{2}=\cdots=p_{n}=1 / n$이라고 가정하자. $E_{i}$를 수집된 $n$개의 쿠폰 중에 유형 $i$ 쿠폰이 없는 사건이라고 하자. 사건들의 합집합의 확률에 대한 포함-배제 원리($P\left(\cup_{i} E_{i}\right)$)를 적용하여 다음 항등식을 증명하라.n!=\sum_{k=0}^{n}(-1)^{k}\binom{n}{k}(n-k)^{n}
3.30. 임의의 사건 $E$와 $F$에 대해 다음을 보여라.P(E \mid E \cup F) \geq P(E \mid F)
힌트: $F$가 발생하는지 여부에 따라 조건화하여 $P(E \mid E \cup F)$를 계산하라. 3.31. 사건 $A$가 발생할 확률은 60%이다. $A$가 발생하지 않으면 $B$가 발생할 확률은 10%이다. 사건 $A$ 또는 $B$ 중 적어도 하나가 발생할 확률은 얼마인가? ## Chapter ## Random Variables ## 4 ## Contents 4.1 **Random Variables** 4.2 **Discrete Random Variables** 4.3 **Expected Value** 4.4 **Expectation of a Function of a Random Variable** 4.5 **Variance** 4.6 **The Bernoulli and Binomial Random Variables** 4.7 **The Poisson Random Variable** 4.8 **Other Discrete Probability Distributions** 4.9 **Expected Value of Sums of Random Variables** 4.10 **Properties of the Cumulative Distribution Function** ### 4.1 Random Variables 실험을 수행할 때, 우리는 실제 결과 자체보다는 **결과의 어떤 함수**에 주로 관심을 갖는 경우가 많다. 예를 들어, 주사위를 던질 때 우리는 각 주사위의 개별 값보다는 두 주사위의 합에 관심이 있는 경우가 많다. 즉, 합이 7이라는 사실에 관심이 있을 수 있으며, 실제 결과가 $(1,6), (2,5), (3,4), (4,3), (5,2)$ 또는 $(6,1)$이었는지에 대해서는 신경 쓰지 않을 수 있다. 또한, 동전을 던질 때 우리는 전체 앞면의 개수에 관심이 있을 수 있으며, 실제 앞면-뒷면 시퀀스가 어떻게 나왔는지에 대해서는 전혀 신경 쓰지 않을 수 있다. 이러한 관심 있는 양, 또는 더 형식적으로는 **표본 공간에 정의된 실수 값 함수**를 **확률 변수(random variables)**라고 한다. 확률 변수의 값은 실험의 결과에 의해 결정되므로, 우리는 확률 변수의 가능한 값에 확률을 할당할 수 있다. ## Example Ia 3개의 공정한 동전을 던지는 실험을 가정해 보자. $Y$를 앞면이 나타나는 횟수라고 하면, $Y$는 0, 1, 2, 3 중 하나의 값을 가지는 **확률 변수(random variable)**이며, 각 값에 대한 확률은 다음과 같다.\begin{aligned} & P{Y=0}=P{(T, T, T)}=\frac{1}{8} \ & P{Y=1}=P{(T, T, H),(T, H, T),(H, T, T)}=\frac{3}{8} \ & P{Y=2}=P{(T, H, H),(H, T, H),(H, H, T)}=\frac{3}{8} \ & P{Y=3}=P{(H, H, H)}=\frac{1}{8} \end{aligned}
$Y$는 반드시 0부터 3까지의 값 중 하나를 가져야 하므로, 다음이 성립해야 한다.1=P\left(\bigcup_{i=0}^{3}{Y=i}\right)=\sum_{i=0}^{3} P{Y=i}
이는 물론 앞서 제시된 확률들과 일치한다. ## Example Ib 한 생명 보험 설계사에게는 두 명의 고령 고객이 있으며, 각 고객은 사망 시 100,000달러를 지급하는 생명 보험에 가입되어 있다. **Y**를 젊은 고객이 다음 해에 사망할 사건이라고 하고, **O**를 나이 많은 고객이 다음 해에 사망할 사건이라고 하자. **Y**와 **O**는 독립이며, 각각의 확률은 $P(Y)=.05$ 및 $P(O)=.10$이라고 가정한다. **X**가 올해 이 고객들의 수혜자에게 지급될 총 금액(100,000달러 단위)을 나타낸다면, **X**는 $0, 1, 2$ 중 하나의 값을 가질 수 있는 확률 변수이며, 각각의 확률은 다음과 같다:\begin{aligned} & P{X=0}=P\left(Y^{c} O^{c}\right)=P\left(Y^{c}\right) P\left(O^{c}\right)=(.95)(.9)=.855 \ & P{X=1}=P\left(Y O^{c}\right)+P\left(Y^{c} O\right)=(.05)(.9)+(.95)(.1)=.140 \ & P{X=2}=P(Y O)=(.05)(.1)=.005 \end{aligned}
1부터 20까지 번호가 매겨진 20개의 공이 들어 있는 항아리에서 4개의 공을 비복원 추출 방식으로 무작위로 선택한다. **X**가 선택된 공 중 가장 큰 번호의 공이라면, **X**는 $4, 5, \ldots, 20$ 중 하나의 값을 가질 수 있는 확률 변수이다. 20개의 공 중 4개를 선택하는 $\binom{20}{4}$가지 가능한 선택 각각이 동일하게 가능하므로, **X**가 각 가능한 값을 가질 확률은 다음과 같다:P{X=i}=\frac{\binom{i-1}{3}}{\binom{20}{4}}, \quad i=4, \ldots, 20
이는 **X**=$i$가 되는 선택의 수는 번호 $i$가 매겨진 공과 1부터 $i-1$까지 번호가 매겨진 공 중 3개가 선택되는 선택의 수와 같기 때문이다. 이러한 선택은 $\binom{1}{1}\binom{i-1}{3}$가지가 있으므로, 위 방정식이 성립한다. 이제 $P\{X>10\}$을 결정하고 싶다고 가정해 보자. 한 가지 방법은 물론 위 식을 사용하여 다음과 같이 얻는 것이다:P{X>10}=\sum_{i=11}^{20} P{X=i}=\sum_{i=11}^{20} \frac{\binom{i-1}{3}}{\binom{20}{4}}
그러나 $P(X>10)$을 결정하는 더 직접적인 접근 방식은 다음을 사용하는 것이다:P{X>10}=1-P{X \leq 10}=1-\frac{\binom{10}{4}}{\binom{20}{4}}
이는 선택된 4개의 공이 1부터 10까지 번호가 매겨진 공들 중에서 나올 때 **X**가 10보다 작거나 같을 것이기 때문에 위 결과가 도출된다. ## Example 앞면이 나올 확률이 $p$인 동전을 던지는 독립적인 시행을 앞면이 나오거나 총 $n$번의 던지기가 이루어질 때까지 계속 수행한다. 동전을 던진 횟수를 $X$라고 하면, $X$는 $1, 2, 3, \ldots, n$ 중 하나의 값을 취하는 확률 변수이며, 각각의 확률은 다음과 같다.\begin{aligned} P{X=1} & =P{H}=p \ P{X=2} & =P{(T, H)}=(1-p) p \ P{X=3} & =P{(T, T, H)}=(1-p)^{2} p \ & \cdot \ & \cdot \ P{X=n-1} & =P{(\underbrace{T, T, \ldots, T,}{n-2} H)}=(1-p)^{n-2} p \ P{X=n} & =P{(\underbrace{T, T, \ldots, T,}{n-1} T),(\underbrace{T, T, \ldots, T,}_{n-1} H)}=(1-p)^{n-1} \end{aligned}
\begin{aligned} P\left(\bigcup_{i=1}^{n}{X=i}\right) & =\sum_{i=1}^{n} P{X=i} \ & =\sum_{i=1}^{n-1} p(1-p)^{i-1}+(1-p)^{n-1} \ & =p\left[\frac{1-(1-p)^{n-1}}{1-(1-p)}\right]+(1-p)^{n-1} \ & =1-(1-p)^{n-1}+(1-p)^{n-1} \ & =1 \end{aligned} $$
예제 1e
개의 서로 다른 종류의 쿠폰이 있고, 쿠폰을 얻을 때마다 이전 선택과 독립적으로 가지 종류 중 어느 하나일 확률이 동일하다고 가정하자. 관심 있는 확률 변수 중 하나는 , 즉 각 종류의 쿠폰을 적어도 하나씩 모두 모을 때까지 수집해야 하는 쿠폰의 수이다. 을 직접 유도하기보다는, 가 보다 클 확률을 고려하는 것부터 시작하자. 이를 위해 을 고정하고 다음과 같이 사건 을 정의한다: 는 수집된 첫 개의 쿠폰 중 종류의 쿠폰이 포함되지 않는 사건이다 (). 따라서,
이제, 는 수집된 개의 쿠폰 각각이 종류가 아닐 경우 발생한다. 각 쿠폰이 종류가 아닐 확률은 이므로, 연속적인 쿠폰 종류의 독립성을 가정하면 다음과 같다.
또한, 사건 는 수집된 첫 개의 쿠폰 중 종류 또는 종류가 없을 경우 발생한다. 따라서, 다시 독립성을 사용하여 다음을 알 수 있다.
동일한 추론을 통해 다음을 얻는다.
그리고 일 때 다음을 알 수 있다.
가 과 같을 확률은 이제 다음 공식을 사용하여 이전 공식으로부터 얻을 수 있다.
또는, 동등하게,
관심 있는 또 다른 확률 변수는 첫 번의 선택에 포함된 서로 다른 종류의 쿠폰 수이다. 이 확률 변수를 이라고 부르자. 를 계산하기 위해, 먼저 개의 서로 다른 종류의 특정 집합에 초점을 맞추고, 이 집합이 첫 번의 선택에서 얻은 서로 다른 종류의 집합을 구성할 확률을 결정하자. 이제, 이러한 상황이 되기 위해서는 얻은 첫 개의 쿠폰이 다음 조건을 만족해야 한다.
\begin{array}{ll} A: & \text { 각각이 이 } k \text {가지 종류 중 하나일 것 } \\ B: & \text { 이 } k \text>가지 종류 각각이 표현될 것 } \end{array}이제, 선택된 각 쿠폰이 가지 종류 중 하나일 확률은 이므로, 가 유효할 확률은 이다. 또한, 고려 중인 가지 종류 중 하나인 쿠폰이 주어졌을 때, 이 가지 종류 중 어느 하나일 확률이 동일하다는 것을 쉽게 알 수 있다. 따라서, 가 발생했을 때 의 조건부 확률은 가지 가능한 종류 중 어느 하나일 확률이 동일한 개의 쿠폰 집합이 모든 가지 종류의 완전한 집합을 포함할 확률과 동일하다. 그러나 이것은 가지 종류 중에서 선택할 때 완전한 집합을 모으는 데 필요한 수가 보다 작거나 같을 확률이며, 따라서 대신 를 사용하여 방정식 (1.1)로부터 얻을 수 있다. 따라서, 다음을 얻는다.
마지막으로, 가지 종류의 집합에 대해 가지 가능한 선택이 있으므로, 다음을 얻는다.
비고 완전한 집합을 얻으려면 적어도 개의 쿠폰을 수집해야 하므로, 이면 이다. 따라서, 방정식 (1.1)로부터 정수 에 대해 흥미로운 조합론적 항등식을 얻는다.
이는 다음과 같이 쓸 수 있다.
또는, 을 곱하고 로 두면,
\sum_{j=1}^{N}\binom{N}{j} j^{n}(-1)^{j-1}=0 \quad 1 \leq n<N $$ $\square$ 확률 변수 $X$에 대해, 다음과 같이 정의된 함수 $F$는F(x)=P{X \leq x} \quad-\infty<x<\infty
$X$의 **누적 분포 함수(cumulative distribution function)** 또는 간단히 **분포 함수(distribution function)**라고 불린다. 따라서, 분포 함수는 모든 실수 값 $x$에 대해 확률 변수가 $x$보다 작거나 같을 확률을 지정한다. 이제, $a \leq b$라고 가정하자. 그러면 사건 $\{X \leq a\}$가 사건 $\{X \leq b\}$에 포함되므로, 전자의 확률인 $F(a)$는 후자의 확률인 $F(b)$보다 작거나 같다는 결론이 나온다. 다시 말해, $F(x)$는 $x$에 대한 **비감소 함수(nondecreasing function)**이다. 분포 함수의 다른 일반적인 속성은 섹션 4.10에 설명되어 있다. ### 4.2 Discrete Random Variables 가능한 값의 개수가 많아야 가산(countable)인 확률 변수를 **이산 확률 변수(discrete random variable)**라고 한다. 이산 확률 변수 $X$에 대해 $X$의 **확률 질량 함수(probability mass function)** $p(a)$를 다음과 같이 정의한다.p(a)=P{X=a}
확률 질량 함수 $p(a)$는 많아야 가산 개수의 $a$ 값에 대해서만 양수이다. 즉, $X$가 $x_{1}, x_{2}, \ldots$ 중 하나의 값을 취해야 한다면,\begin{array}{ll} p\left(x_{i}\right) \geq 0 & \text { for } i=1,2, \ldots \ p(x)=0 & \text { for all other values of } x \end{array}
$X$는 $x_{i}$ 값 중 하나를 취해야 하므로, 다음이 성립한다.\sum_{i=1}^{\infty} p\left(x_{i}\right)=1
확률 질량 함수를 $x$-축에 $x_{i}$를, $y$-축에 $p\left(x_{i}\right)$를 플로팅하여 그래픽 형식으로 나타내는 것이 종종 유익하다. 예를 들어, $X$의 확률 질량 함수가 다음과 같다고 하자.p(0)=\frac{1}{4} \quad p(1)=\frac{1}{2} \quad p(2)=\frac{1}{4}
이 함수는 그림 4.1과 같이 그래픽으로 표현할 수 있다. 마찬가지로, 두 개의 주사위를 굴렸을 때의 합을 나타내는 확률 변수의 확률 질량 함수 그래프는 그림 4.2와 같다. 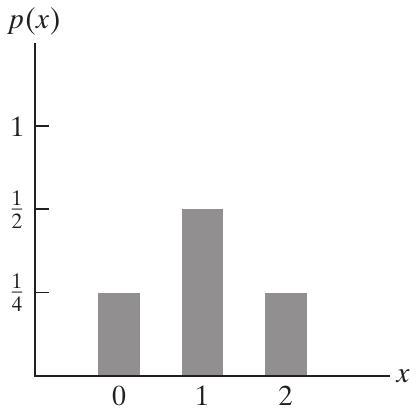 Figure 4.1  Figure 4.2 예제 2a 확률 변수 $X$의 확률 질량 함수는 $p(i)=c \lambda^{i} / i!$, $i=0,1,2, \ldots$로 주어지며, 여기서 $\lambda$는 양수 값이다. (a) $P\{X=0\}$와 (b) $P\{X>2\}$를 구하시오. 풀이 $\sum_{i=0}^{\infty} p(i)=1$이므로, 다음이 성립한다.c \sum_{i=0}^{\infty} \frac{\lambda^{i}}{i!}=1
$e^{x}=\sum_{i=0}^{\infty} x^{i} / i!$이므로, 이는 다음을 의미한다.c e^{\lambda}=1 \quad \text { or } \quad c=e^{-\lambda}
따라서, (a) $P\{X=0\}=e^{-\lambda} \lambda^{0} / 0!=e^{-\lambda}$ (b) $P\{X>2\}=1-P\{X \leq 2\}=1-P\{X=0\}-P\{X=1\}$\begin{aligned} & -P{X=2} \ = & 1-e^{-\lambda}-\lambda e^{-\lambda}-\frac{\lambda^{2} e^{-\lambda}}{2} \end{aligned}
**누적 분포 함수(cumulative distribution function)** $F$는 $p(a)$를 사용하여 다음과 같이 표현할 수 있다.F(a)=\sum_{\text {all } x \leq a} p(x)
가능한 값이 $x_{1}, x_{2}, x_{3}, \ldots$이고 $x_{1}<x_{2}<x_{3}<\cdots$인 이산 확률 변수 $X$의 분포 함수 $F$는 **계단 함수(step function)**이다. 즉, $F$의 값은 구간 ($x_{i-1}, x_{i}$)에서 일정하며, $x_{i}$에서 $p\left(x_{i}\right)$ 크기의 계단(또는 점프)을 취한다. 예를 들어, $X$의 확률 질량 함수가 다음과 같이 주어졌다고 하자.p(1)=\frac{1}{4} \quad p(2)=\frac{1}{2} \quad p(3)=\frac{1}{8} \quad p(4)=\frac{1}{8}
F(a)= \begin{cases}0 & a<1 \ \frac{1}{4} & 1 \leq a<2 \ \frac{3}{4} & 2 \leq a<3 \ \frac{7}{8} & 3 \leq a<4 \ 1 & 4 \leq a\end{cases}
이 함수는 그림 4.3에 그래픽으로 나타나 있다.  Figure 4.3 값 1, 2, 3, 4 중 어느 하나에서의 계단 크기는 $X$가 해당 특정 값을 취할 확률과 같다는 점에 유의하라. ### 4.3 Expected Value 확률 이론에서 가장 중요한 개념 중 하나는 **확률 변수의 기댓값(expectation)**이다. $X$가 확률 질량 함수 $p(x)$를 갖는 이산 확률 변수일 때, $X$의 기댓값 또는 기대치(expected value)는 $E[X]$로 표기하며 다음과 같이 정의된다.E[X]=\sum_{x: p(x)>0} x p(x)
다시 말해, $X$의 기댓값은 $X$가 가질 수 있는 가능한 값들의 **가중 평균**이며, 각 값은 $X$가 그 값을 취할 확률에 의해 가중된다. 예를 들어, $X$의 확률 질량 함수가 다음과 같이 주어지면p(0)=\frac{1}{2}=p(1)
E[X]=0\left(\frac{1}{2}\right)+1\left(\frac{1}{2}\right)=\frac{1}{2}
는 $X$가 가질 수 있는 두 가지 가능한 값인 0과 1의 **일반적인 평균**이다. 반면에, 만약p(0)=\frac{1}{3} \quad p(1)=\frac{2}{3}
E[X]=0\left(\frac{1}{3}\right)+1\left(\frac{2}{3}\right)=\frac{2}{3}
는 두 가지 가능한 값인 0과 1의 가중 평균이며, $p(1)=2 p(0)$이므로 값 1에는 값 0보다 두 배의 가중치가 부여된다. 기댓값 정의에 대한 또 다른 동기는 **확률의 빈도 해석(frequency interpretation)**에서 찾을 수 있다. 이 해석(8장에서 제시될 대수의 강법칙(strong law of large numbers)에 의해 부분적으로 정당화됨)은 실험의 독립적인 반복이 무한히 수행될 경우, 어떤 사건 $E$에 대해서든 $E$가 발생하는 시간의 비율이 $P(E)$가 될 것이라고 가정한다. 이제, 각각 $p\left(x_{1}\right), p\left(x_{2}\right), \ldots, p\left(x_{n}\right)$의 확률로 $x_{1}, x_{2}, \ldots x_{n}$ 중 하나의 값을 취해야 하는 확률 변수 $X$를 고려하고, $X$를 한 번의 우연 게임에서 얻는 상금으로 생각해보자. 즉, 확률 $p\left(x_{i}\right)$로 우리는 $x_{i}$ 단위를 얻게 된다 ($i=1,2, \ldots, n$). 빈도 해석에 따르면, 이 게임을 계속해서 플레이한다면, 우리가 $x_{i}$를 얻는 시간의 비율은 $p\left(x_{i}\right)$가 될 것이다. 이것이 모든 $i, i=1,2, \ldots, n$에 대해 참이므로, 게임당 평균 상금은 다음과 같을 것이다.\sum_{i=1}^{n} x_{i} p\left(x_{i}\right)=E[X]
공정한 주사위를 굴렸을 때의 결과인 $X$에 대해 $E[X]$를 구하시오. 풀이 $p(1)=p(2)=p(3)=p(4)=p(5)=p(6)=\frac{1}{6}$이므로, 다음을 얻는다.E[X]=1\left(\frac{1}{6}\right)+2\left(\frac{1}{6}\right)+3\left(\frac{1}{6}\right)+4\left(\frac{1}{6}\right)+5\left(\frac{1}{6}\right)+6\left(\frac{1}{6}\right)=\frac{7}{2}
## Example 3b ## 3c 예시 $I$가 사건 $A$에 대한 **지표 변수(indicator variable)**라고 하는 것은 다음과 같다:I= \begin{cases}1 & \text { if } A \text { occurs } \ 0 & \text { if } A^{c} \text { occurs }\end{cases}
$E[I]$를 구하시오. 풀이 $p(1)=P(A), p(0)=1-P(A)$이므로, 다음을 얻는다:E[I]=P(A)
즉, 사건 $A$에 대한 지표 변수의 **기댓값(expected value)**은 $A$가 발생할 확률과 같다. $\square$ 퀴즈 쇼 참가자가 두 가지 질문(질문 1과 질문 2)을 받는데, 그는 자신이 선택한 순서대로 답을 시도해야 한다. 만약 그가 질문 $i$를 먼저 시도하기로 결정하면, 질문 $i$에 대한 답이 맞았을 경우에만 질문 $j, j \neq i$로 넘어갈 수 있다. 만약 그의 첫 번째 답이 틀리면, 다른 질문에 답할 수 없다. 참가자는 질문 $i$에 올바르게 답하면 $V_i$ 달러를 받는다 ($i=1,2$). 예를 들어, 두 질문 모두에 올바르게 답하면 $V_1+V_2$ 달러를 받는다. 질문 $i$에 대한 답을 알고 있을 확률이 $P_i$라고 할 때 ($i=1,2$), **기대 상금(expected winnings)**을 최대화하기 위해 어떤 질문을 먼저 시도해야 하는가? 그가 질문 $i$에 대한 답을 알고 있는 사건 $E_i$ ($i=1,2$)는 **독립 사건(independent events)**이라고 가정한다. 풀이 한편, 그가 질문 1을 먼저 시도한다면, 그는 다음을 얻는다:\begin{array}{ll} 0 & \text { 확률 } 1-P_{1} \text{로} \ V_{1} & \text { 확률 } P_{1}\left(1-P_{2}\right) \text{로} \ V_{1}+V_{2} & \text { 확률 } P_{1} P_{2} \text{로} \end{array}
V_{1} P_{1}\left(1-P_{2}\right)+\left(V_{1}+V_{2}\right) P_{1} P_{2}
V_{2} P_{2}\left(1-P_{1}\right)+\left(V_{1}+V_{2}\right) P_{1} P_{2}
V_{1} P_{1}\left(1-P_{2}\right) \geq V_{2} P_{2}\left(1-P_{1}\right)
\frac{V_{1} P_{1}}{1-P_{1}} \geq \frac{V_{2} P_{2}}{1-P_{2}}
400=\frac{(100)(.8)}{.2}>\frac{(200)(.6)}{.4}=300 $$
Example 3d
120명의 학생으로 구성된 한 학급이 3대의 버스를 타고 교향악 공연을 보러 간다. 한 버스에는 36명, 다른 버스에는 40명, 세 번째 버스에는 44명의 학생이 탑승한다. 버스가 도착했을 때, 120명의 학생 중 한 명이 무작위로 선택된다. 무작위로 선택된 학생이 탑승한 버스의 학생 수를 라고 할 때, 를 구하시오.
풀이 무작위로 선택된 학생이 120명의 학생 중 누구라도 될 확률이 동일하므로, 다음이 성립한다.
따라서,
그러나 버스 한 대당 평균 학생 수는 명이며, 이는 무작위로 선택된 학생이 탑승한 버스의 기댓값이 버스 한 대당 평균 학생 수보다 크다는 것을 보여준다. 이는 일반적인 현상이며, 버스에 학생 수가 많을수록 무작위로 선택된 학생이 그 버스에 탑승했을 가능성이 더 높기 때문에 발생한다. 결과적으로, 학생 수가 많은 버스에는 학생 수가 적은 버스보다 더 많은 가중치가 부여된다. (Self-Test Problem 4.4 참조)
비고 기댓값의 확률 개념은 질량 분포의 무게 중심이라는 물리적 개념과 유사하다. 확률 질량 함수 를 갖는 이산 확률 변수 를 고려해보자. 이제 질량 를 갖는 추들이 점 에 위치한 무게 없는 막대를 상상한다면(Figure 4.4 참조), 막대가 균형을 이루는 지점은 무게 중심으로 알려져 있다. 초등 정역학에 익숙한 독자라면 이 지점이 에 있다는 것을 쉽게 보일 수 있다.
 Figure 4.4
Figure 4.4
4.4 Expectation of a Function of a Random Variable
이산 확률 변수와 그 확률 질량 함수가 주어졌을 때, 의 어떤 함수, 예를 들어 의 기댓값을 계산하고 싶다고 가정해 보자. 어떻게 이를 수행할 수 있을까? 한 가지 방법은 다음과 같다: 자체가 이산 확률 변수이므로, 의 확률 질량 함수로부터 결정될 수 있는 확률 질량 함수를 갖는다. 의 확률 질량 함수를 결정한 후에는 기댓값의 정의를 사용하여 를 계산할 수 있다.
예제 4a
명제 4.1
확률 변수 가 다음 확률로 값 중 하나를 취한다고 하자.
를 계산하라. 풀이 라고 하자. 그러면 의 확률 질량 함수는 다음과 같다.
따라서,
다음 사항에 유의하라.
앞선 절차는 의 확률 질량 함수를 알면 의 어떤 함수의 기댓값도 항상 계산할 수 있게 해주지만, 에 대해 생각하는 또 다른 방법이 있다: 가 와 같을 때마다 는 와 같아지므로, 는 값들의 가중 평균이어야 하며, 는 가 와 같을 확률로 가중되어야 한다는 것이 합리적으로 보인다. 즉, 다음 결과는 매우 직관적이다. 가 값 중 하나를 각각의 확률 로 취하는 이산 확률 변수라면, 임의의 실수 값 함수 에 대해,
이 명제를 증명하기 전에, 예제 4a의 결과와 일치하는지 확인해 보자. 이 명제를 해당 예제에 적용하면 다음과 같다.
이는 예제 4a에서 주어진 결과와 일치한다.
명제 4.1의 증명 명제 4.1의 증명은 앞선 확인과 마찬가지로, 에서 의 값이 같은 모든 항을 함께 묶음으로써 진행된다. 구체적으로, 가 의 서로 다른 값들을 나타낸다고 가정하자. 그러면, 같은 값을 갖는 모든 를 묶으면 다음과 같다.
Example 4b
계절 상품은 판매된 단위당 달러의 순이익을 내고, 시즌이 끝났을 때 팔리지 않고 남은 단위당 달러의 순손실을 발생시킨다. 특정 백화점에서 한 시즌 동안 주문되는 상품의 단위 수는 확률 질량 함수 를 갖는 확률 변수이다. 만약 백화점이 이 상품을 미리 재고로 확보해야 한다면, 기대 이익을 최대화하기 위해 몇 단위를 재고로 확보해야 하는가?
해답 를 주문된 단위 수라고 하자. 만약 단위를 재고로 확보한다면, 이익(라고 부르자)은 다음과 같이 표현될 수 있다.
따라서 기대 이익은 다음과 같다.
최적의 값을 결정하기 위해, 를 1단위 증가시켰을 때 이익에 어떤 변화가 생기는지 살펴보자. 대입을 통해 이 경우의 기대 이익은 다음과 같음을 알 수 있다.
그러므로,
따라서 다음 조건이 충족될 때 단위를 재고로 확보하는 것이 단위를 재고로 확보하는 것보다 더 나을 것이다.
식 (4.1)의 좌변은 에 대해 증가하는 반면 우변은 상수이므로, 이 부등식은 인 모든 값에 대해 만족될 것이다. 여기서 는 식 (4.1)을 만족하는 의 가장 큰 값이다.
이므로, 개의 품목을 재고로 확보하는 것이 최대 기대 이익으로 이어질 것이다.
Example
4c
Utility
개의 결과() 중 하나를 초래할 수 있는 두 가지 가능한 행동 중 하나를 선택해야 한다고 가정해 보자. 첫 번째 행동을 선택하면 결과 가 확률 로 발생하고(), 두 번째 행동을 선택하면 결과 가 확률 로 발생한다고 가정하자(). 여기서 이다. 다음 접근 방식을 사용하여 어떤 행동을 선택할지 결정할 수 있다.
먼저, 다른 결과에 수치 값을 할당하는 것부터 시작한다. 가장 바람직하지 않은 결과와 가장 바람직한 결과를 각각 와 라고 부르자. 결과 에는 값 0을 부여하고, 에는 값 1을 부여한다. 이제 나머지 개의 결과 중 하나인 를 고려해 보자. 이 결과를 평가하기 위해, 를 받거나, 확률 로 결과 를 얻거나 확률 로 결과 를 얻는 무작위 실험에 참여하는 것 중 하나를 선택해야 한다고 상상해 보자.
분명히 당신의 선택은 의 값에 따라 달라질 것이다. 한편으로, 만약 이라면, 실험은 확실히 결과 를 초래할 것이고, 가 가장 바람직한 결과이므로, 당신은 를 받는 것보다 실험에 참여하는 것을 선호할 것이다. 다른 한편으로, 만약 이라면, 실험은 가장 바람직하지 않은 결과인 를 초래할 것이므로, 이 경우 당신은 실험에 참여하는 것보다 결과 를 선호할 것이다.
이제 가 1에서 0으로 감소함에 따라, 당신의 선택은 어느 시점에서 실험 참여에서 의 확실한 반환으로 전환될 것이며, 그 임계 전환점에서 당신은 두 대안에 대해 무관심할 것이라는 것이 합리적으로 보인다. 그 무관심 확률 를 결과 의 값으로 취한다. 다시 말해, 의 값은 당신이 결과 를 받거나, 확률 로 결과 를 얻거나 확률 로 결과 를 얻는 실험에 참여하는 것 중 무관심하게 되는 확률 이다. 우리는 이 무관심 확률을 결과 의 **효용(utility)**이라고 부르며, 로 표기한다.
어떤 행동이 더 우월한지 결정하기 위해, 우리는 각각의 행동을 평가해야 한다. 첫 번째 행동을 고려해 보자. 이 행동은 확률 로 결과 를 초래한다(). 우리는 이 행동의 결과를 2단계 실험에 의해 결정되는 것으로 생각할 수 있다. 첫 번째 단계에서는 확률에 따라 값 중 하나가 선택된다. 만약 값 가 선택되면, 당신은 결과 를 받는다. 그러나 는 확률 로 결과 를 얻거나 확률 로 결과 를 얻는 것과 동등하므로, 2단계 실험의 결과는 결과 또는 결과 가 얻어지는 실험과 동등하며, 는 다음 확률로 얻어진다.
마찬가지로, 두 번째 행동을 선택한 결과는 결과 또는 결과 가 얻어지는 실험에 참여하는 것과 동등하며, 는 다음 확률로 얻어진다.
가 보다 선호되므로, 다음이 성립하면 첫 번째 행동이 두 번째 행동보다 선호된다.
다시 말해, 행동의 가치는 그 결과의 효용의 **기대값(expected value)**으로 측정될 수 있으며, 가장 큰 기대 효용을 가진 행동이 가장 선호된다.
명제 4.1의 간단한 논리적 결과는 따름정리 4.1이다.
Corollary
4.1
와 가 상수일 때,
Proof
\begin{aligned} E[a X+b] & =\sum_{x: p(x)>0}(a x+b) p(x) \\ & =a \sum_{x: p(x)>0} x p(x)+b \sum_{x: p(x)>0} p(x) \\ & =a E[X]+b \end{aligned} $$ $\square$ 확률 변수 $X$의 **기댓값(expected value)** $E[X]$는 $X$의 **평균(mean)** 또는 **1차 모멘트(first moment)**라고도 불린다. $n \geq 1$일 때, $E\left[X^{n}\right]$는 $X$의 **n차 모멘트(nth moment)**라고 한다. 명제 4.1에 따라 다음을 알 수 있다.E\left[X^{n}\right]=\sum_{x: p(x)>0} x^{n} p(x)
### 4.5 Variance 확률 변수 $X$와 그 분포 함수 $F$가 주어졌을 때, $F$의 본질적인 특성을 적절하게 정의된 특정 측도로 요약할 수 있다면 매우 유용할 것이다. 그러한 측도 중 하나는 $X$의 기댓값인 $E[X]$이다. 그러나 $E[X]$는 $X$의 가능한 값들의 가중 평균을 제공하지만, 이러한 값들의 **변동(variation)** 또는 **분산(spread)**에 대해서는 아무것도 알려주지 않는다. 예를 들어, 다음과 같이 확률 질량 함수가 결정되는 확률 변수 $W, Y, Z$는\begin{aligned} W & =0 \quad \text { with probability } 1 \ Y & = \begin{cases}-1 & \text { with probability } \frac{1}{2} \ +1 & \text { with probability } \frac{1}{2}\end{cases} \ Z & = \begin{cases}-100 & \text { with probability } \frac{1}{2} \ +100 & \text { with probability } \frac{1}{2}\end{cases} \end{aligned}
모두 동일한 기댓값, 즉 0을 갖지만, $W$의 가능한 값들(상수임)보다 $Y$의 가능한 값들에서 훨씬 더 큰 분산이 있고, $Y$의 가능한 값들보다 $Z$의 가능한 값들에서 훨씬 더 큰 분산이 있다. 우리는 $X$가 평균 $E[X]$ 주변의 값을 취할 것으로 예상하므로, $X$의 가능한 변동을 측정하는 합리적인 방법은 $X$가 평균으로부터 평균적으로 얼마나 떨어져 있는지를 살펴보는 것일 것이다. 이 변동을 측정하는 한 가지 가능한 방법은 $\mu= E[X]$일 때, $E[|X-\mu|]$라는 양을 고려하는 것이다. 그러나 이 양을 다루는 것은 수학적으로 불편한 것으로 밝혀졌으므로, 일반적으로 더 다루기 쉬운 양, 즉 $X$와 그 평균 사이의 차이의 제곱에 대한 기댓값이 고려된다. 따라서 우리는 다음 정의를 갖는다. ## Definition $X$가 평균이 $\mu$인 확률 변수일 때, $X$의 분산은 $\operatorname{Var}(X)$로 표기하며 다음과 같이 정의된다.\operatorname{Var}(X)=E\left[(X-\mu)^{2}\right]
$\operatorname{Var}(X)$에 대한 대체 공식은 다음과 같이 유도된다.\begin{aligned} \operatorname{Var}(X) & =E\left[(X-\mu)^{2}\right] \ & =\sum_{x}(x-\mu)^{2} p(x) \ & =\sum_{x}\left(x^{2}-2 \mu x+\mu^{2}\right) p(x) \ & =\sum_{x} x^{2} p(x)-2 \mu \sum_{x} x p(x)+\mu^{2} \sum_{x} p(x) \ & =E\left[X^{2}\right]-2 \mu^{2}+\mu^{2} \ & =E\left[X^{2}\right]-\mu^{2} \end{aligned}
\operatorname{Var}(X)=E\left[X^{2}\right]-(E[X])^{2}
말로 설명하면, **$X$의 분산은 $X^{2}$의 기댓값에서 $X$의 기댓값의 제곱을 뺀 것과 같다.** 실제로 이 공식은 $\operatorname{Var}(X)$를 계산하는 가장 쉬운 방법을 제공하는 경우가 많다. ## Example 공정한 주사위를 굴렸을 때의 결과를 $X$라고 할 때, $\operatorname{Var}(X)$를 계산하시오. 풀이 예제 3a에서 $E[X]=\frac{7}{2}$임을 보였다. 또한,\begin{aligned} E\left[X^{2}\right] & =1^{2}\left(\frac{1}{6}\right)+2^{2}\left(\frac{1}{6}\right)+3^{2}\left(\frac{1}{6}\right)+4^{2}\left(\frac{1}{6}\right)+5^{2}\left(\frac{1}{6}\right)+6^{2}\left(\frac{1}{6}\right) \ & =\left(\frac{1}{6}\right) \end{aligned}
\operatorname{Var}(X)=\frac{91}{6}-\left(\frac{7}{2}\right)^{2}=\frac{35}{12}
유용한 항등식은 임의의 상수 $a$와 $b$에 대해 다음과 같다.\operatorname{Var}(a X+b)=a^{2} \operatorname{Var}(X)
이 등식을 증명하기 위해, $\mu=E[X]$라고 하고, Corollary 4.1로부터 $E[a X+b]= a \mu+b$임을 주목하자. 그러므로,\begin{aligned} \operatorname{Var}(a X+b) & =E\left[(a X+b-a \mu-b)^{2}\right] \ & =E\left[a^{2}(X-\mu)^{2}\right] \ & =a^{2} E\left[(X-\mu)^{2}\right] \ & =a^{2} \operatorname{Var}(X) \end{aligned}
비고 (a) 평균이 질량 분포의 무게 중심과 유사하게, **분산**은 역학 용어로 **관성 모멘트**를 나타낸다. (b) $\operatorname{Var}(X)$의 제곱근을 $X$의 **표준 편차(standard deviation)**라고 하며, $\mathrm{SD}(X)$로 표기한다. 즉,\operatorname{SD}(X)=\sqrt{\operatorname{Var}(X)}
이산 확률 변수는 종종 **확률 질량 함수(probability mass function)**에 따라 분류된다. 다음 몇 섹션에서는 더 일반적인 유형 중 일부를 살펴본다. ### 4.6 The Bernoulli and Binomial Random Variables 결과가 성공 또는 실패로 분류될 수 있는 시행 또는 실험이 수행된다고 가정해 보자. 결과가 성공일 때 $X=1$이고 실패일 때 $X=0$이라고 하면, $X$의 확률 질량 함수는 다음과 같다.\begin{aligned} & p(0)=P{X=0}=1-p \ & p(1)=P{X=1}=p \end{aligned}
여기서 $p, 0 \leq p \leq 1$는 시행이 성공할 확률이다. 확률 변수 $X$는 어떤 $p \in(0,1)$에 대해 그 확률 질량 함수가 식 (6.1)로 주어질 때 **베르누이 확률 변수**(스위스 수학자 제임스 베르누이의 이름을 따서 명명됨)라고 한다. 이제 각각 확률 $p$로 성공하거나 확률 $1-p$로 실패하는 $n$개의 독립적인 시행이 수행된다고 가정해 보자. 만약 $X$가 $n$개의 시행에서 발생하는 성공의 횟수를 나타낸다면, $X$는 **이항 확률 변수**이며 **모수** ($n, p$)를 갖는다고 한다. 따라서 베르누이 확률 변수는 모수 ($1, p$)를 갖는 이항 확률 변수이다. 모수 ($n, p$)를 갖는 이항 확률 변수의 확률 질량 함수는 다음과 같다.p(i)=\binom{n}{i} p^{i}(1-p)^{n-i} \quad i=0,1, \ldots, n
식 (6.2)의 유효성은 먼저 $i$개의 성공과 $n-i$개의 실패를 포함하는 $n$개의 결과의 특정 시퀀스의 확률이 시행의 독립성 가정에 의해 $p^{i}(1-p)^{n-i}$임을 확인함으로써 검증될 수 있다. 식 (6.2)는 $i$개의 성공과 $n-i$개의 실패로 이어지는 $n$개의 결과의 서로 다른 시퀀스가 $\binom{n}{i}$개 존재하기 때문에 성립한다. 이는 성공으로 이어지는 $i$개의 시행을 선택하는 $\binom{n}{i}$가지의 서로 다른 방법이 있다는 점을 통해 가장 쉽게 이해할 수 있다. 예를 들어, $n=4, i=2$인 경우, 네 번의 시행에서 두 번의 성공이 발생할 수 있는 방법은 $\binom{4}{2}=6$가지이다. 즉, $(s, s, f, f), (s, f, s, f), (s, f, f, s), (f, s, s, f), (f, s, f, s), (f, f, s, s)$와 같은 결과들이 있다. 여기서 $(s, s, f, f)$는 예를 들어 처음 두 번의 시행이 성공이고 마지막 두 번의 시행이 실패임을 의미한다. 이러한 각 결과는 발생 확률이 $p^{2}(1-p)^{2}$이므로, 네 번의 시행에서 두 번의 성공이 발생할 원하는 확률은 $\binom{4}{2} p^{2}(1-p)^{2}$이다. 이항 정리에 의해 확률의 합은 1이 된다는 점에 유의하라. 즉,\sum_{i=0}^{\infty} p(i)=\sum_{i=0}^{n}\binom{n}{i} p^{i}(1-p)^{n-i}=[p+(1-p)]^{n}=1
## Example 6a 동전 5개를 던진다. 결과가 독립적이라고 가정할 때, 앞면이 나오는 횟수의 확률 질량 함수를 구하시오. 풀이 $X$를 앞면(성공)이 나오는 횟수라고 하면, $X$는 모수 $\left(n=5, p=\frac{1}{2}\right)$를 갖는 이항 확률 변수이다. 따라서 식 (6.2)에 의해,\begin{aligned} & P{X=0}=\binom{5}{0}\left(\frac{1}{2}\right)^{0}\left(\frac{1}{2}\right)^{5}=\frac{1}{32} \ & P{X=1}=\binom{5}{1}\left(\frac{1}{2}\right)^{1}\left(\frac{1}{2}\right)^{4}=\frac{5}{32} \ & P{X=2}=\binom{5}{2}\left(\frac{1}{2}\right)^{2}\left(\frac{1}{2}\right)^{3}=\frac{10}{32} \ & P{X=3}=\binom{5}{3}\left(\frac{1}{2}\right)^{3}\left(\frac{1}{2}\right)^{2}=\frac{10}{32} \ & P{X=4}=\binom{5}{4}\left(\frac{1}{2}\right)^{4}\left(\frac{1}{2}\right)^{1}=\frac{5}{32} \ & P{X=5}=\binom{5}{5}\left(\frac{1}{2}\right)^{5}\left(\frac{1}{2}\right)^{0}=\frac{1}{32} \end{aligned}
예제 6b 어떤 회사에서 생산하는 나사가 서로 독립적으로 .01의 확률로 불량품이 되는 것으로 알려져 있다. 이 회사는 나사를 10개씩 묶어 판매하며, 10개의 나사 중 최대 1개만 불량품일 경우 환불을 보장한다. 회사는 판매된 패키지 중 몇 퍼센트를 교체해야 하는가? 풀이 패키지 내 불량 나사의 개수를 $X$라고 하면, $X$는 모수 $(10, .01)$를 갖는 이항 확률 변수이다. 따라서 패키지를 교체해야 할 확률은 다음과 같다.\begin{aligned} 1-P{X=0}-P{X=1} & =1-\binom{10}{0}(.01)^{0}(.99)^{10}-\binom{10}{1}(.01)^{1}(.99)^{9} \ & \approx .004 \end{aligned}
따라서 패키지의 .4퍼센트만이 교체되어야 한다. 예제 6c **Wheel of Fortune** (또는 **Chuck-a-Luck**)으로 알려진 다음 도박 게임은 많은 카니발과 도박 카지노에서 매우 인기가 있다: 플레이어는 1부터 6까지의 숫자 중 하나에 베팅한다. 그런 다음 주사위 3개를 굴려, 플레이어가 베팅한 숫자가 $i$번 나타나면 ($i=1,2,3$), 플레이어는 $i$ 단위를 얻는다. 만약 플레이어가 베팅한 숫자가 주사위 중 어느 것에도 나타나지 않으면, 플레이어는 1 단위를 잃는다. 이 게임은 플레이어에게 공정한가? (실제로는 1부터 6까지의 숫자 중 세 개가 표시된 슬롯에 멈추는 휠을 돌려 게임을 진행하지만, 이 변형은 수학적으로 주사위 버전과 동일하다.) ## Example 6d **풀이** 주사위가 공정하고 서로 독립적으로 작동한다고 가정하면, 베팅한 숫자가 나타나는 횟수는 모수 $\left(3, \frac{1}{6}\right)$를 갖는 **이항 확률 변수(binomial random variable)**이다. 따라서 $X$를 게임에서 플레이어의 상금이라고 하면 다음과 같다.\begin{gathered} P{X=-1}=\binom{3}{0}\left(\frac{1}{6}\right)^{0}\left(\frac{5}{6}\right)^{3}=\frac{125}{216} \ P{X=1}=\binom{3}{1}\left(\frac{1}{6}\right)^{1}\left(\frac{5}{6}\right)^{2}=\frac{75}{216} \ P{X=2}=\binom{3}{2}\left(\frac{1}{6}\right)^{2}\left(\frac{5}{6}\right)^{1}=\frac{15}{216} \ P{X=3}=\binom{3}{3}\left(\frac{1}{6}\right)^{3}\left(\frac{5}{6}\right)^{0}=\frac{1}{216} \end{gathered}
이 게임이 플레이어에게 공정한 게임인지 여부를 결정하기 위해 $E[X]$를 계산해 보자. 앞서 구한 확률로부터 다음을 얻는다.\begin{aligned} E[X] & =\frac{-125+75+30+3}{216} \ & =\frac{-17}{216} \end{aligned}
따라서 장기적으로 볼 때, 플레이어는 216번의 게임당 17단위를 잃게 될 것이다. $\square$ 다음 예시에서는 Gregor Mendel (1822-1884)이 개발한 유전 이론의 가장 간단한 형태를 살펴본다. 어떤 사람의 특정 특성(예: 눈 색깔 또는 왼손잡이)이 한 쌍의 유전자에 의해 분류된다고 가정하고, $d$는 **우성 유전자(dominant gene)**를, $r$은 **열성 유전자(recessive gene)**를 나타낸다고 가정하자. 따라서 $dd$ 유전자를 가진 사람은 **순수 우성(purely dominant)**이고, $rr$ 유전자를 가진 사람은 **순수 열성(purely recessive)**이며, $rd$ 유전자를 가진 사람은 **잡종(hybrid)**이다. 순수 우성 개체와 잡종 개체는 겉모습이 같다. 자녀는 각 부모로부터 1개의 유전자를 받는다. 특정 특성에 대해 2명의 잡종 부모가 총 4명의 자녀를 가질 때, 4명의 자녀 중 3명이 우성 유전자의 겉모습을 가질 확률은 얼마인가? 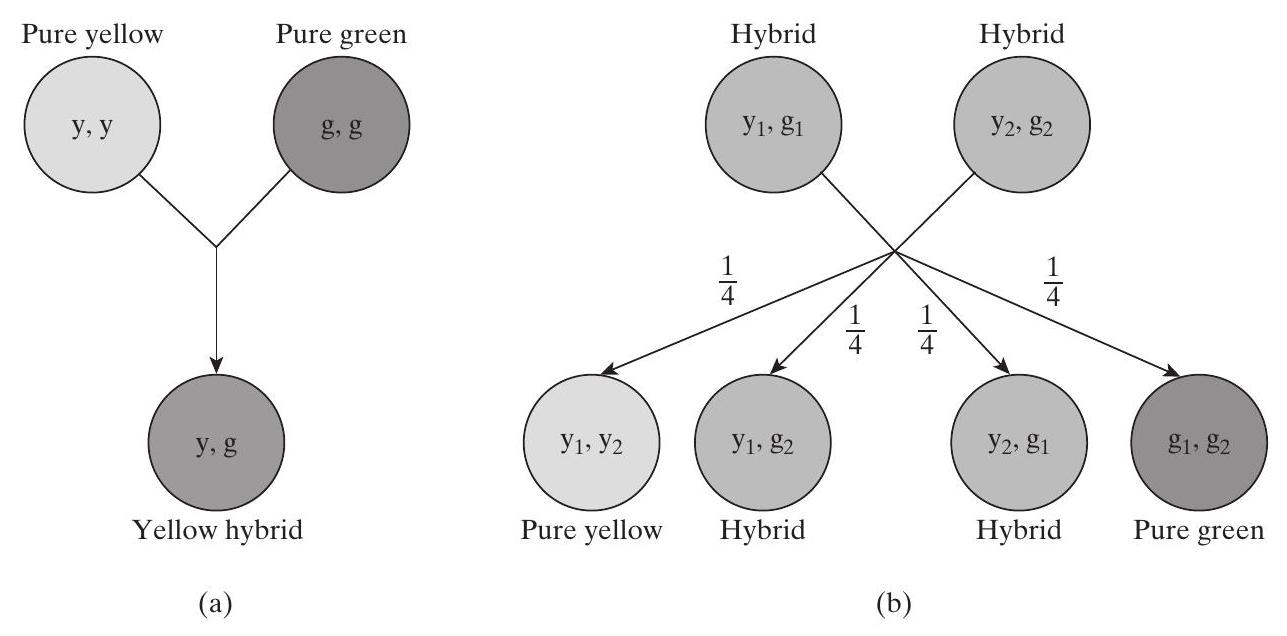 그림 4.5 (a) 순수 노란색 씨앗과 순수 녹색 씨앗의 교배; (b) 잡종 1세대 씨앗의 교배. 앞의 그림 4.5a와 b는 잡종 노란색(우성) 씨앗과 녹색(열성) 씨앗이 교배될 때 어떤 일이 일어날 수 있는지를 보여준다. **풀이** 각 자녀가 각 부모로부터 2개의 유전자 중 하나를 동등하게 물려받을 가능성이 있다고 가정하면, 2명의 잡종 부모의 자녀가 $dd$, $rr$, $rd$ 유전자 쌍을 가질 확률은 각각 $\frac{1}{4}, \frac{1}{4}, \frac{1}{2}$이다. 따라서 자손이 유전자 쌍이 $dd$ 또는 $rd$인 경우 우성 유전자의 겉모습을 가지므로, 그러한 자녀의 수는 모수 $\left(4, \frac{3}{4}\right)$를 갖는 **이항 분포(binomially distributed)**를 따른다. 따라서 원하는 확률은 다음과 같다.\binom{4}{3}\left(\frac{3}{4}\right)^{3}\left(\frac{1}{4}\right)^{1}=\frac{27}{64} $$
Example 6e
배심원 12명 중 8명이 피고인에게 유죄를 선고해야 하는 배심원 재판을 고려해 보자. 즉, 피고인이 유죄 판결을 받으려면 최소 8명의 배심원이 유죄에 투표해야 한다. 배심원들이 독립적으로 행동하고, 피고인의 유무죄와 관계없이 각 배심원이 확률 로 올바른 결정을 내린다고 가정할 때, 배심원이 올바른 결정을 내릴 확률은 얼마인가?
풀이 문제에서 제시된 정보만으로는 해결할 수 없다. 예를 들어, 피고인이 무죄인 경우, 배심원이 올바른 결정을 내릴 확률은 다음과 같다.
반면, 피고인이 유죄인 경우, 올바른 결정을 내릴 확률은 다음과 같다.
따라서, 가 피고인이 유죄일 확률을 나타낸다면, 피고인의 유무죄 여부에 따라 조건화함으로써 배심원이 올바른 결정을 내릴 확률을 얻을 수 있다.
\alpha \sum_{i=8}^{12}\binom{12}{i} \theta^{i}(1-\theta)^{12-i}+(1-\alpha) \sum_{i=5}^{12}\binom{12}{i} \theta^{i}(1-\theta)^{12-i} $$ $\square$ **예제 6f** 통신 시스템은 $n$개의 구성 요소로 이루어져 있으며, 각 구성 요소는 독립적으로 확률 $p$로 작동한다. 전체 시스템은 구성 요소의 절반 이상이 작동할 경우 효과적으로 작동할 수 있다. (a) 5-component 시스템이 3-component 시스템보다 효과적으로 작동할 가능성이 더 높은 $p$ 값은 무엇인가? (b) 일반적으로, $(2 k+1)$-component 시스템이 $(2 k-1)$-component 시스템보다 더 나은 경우는 언제인가? **풀이** (a) 작동하는 구성 요소의 수는 매개변수 $(n, p)$를 갖는 **이항 확률 변수(binomial random variable)**이므로, 5-component 시스템이 효과적일 확률은 다음과 같다.\binom{5}{3} p^{3}(1-p)^{2}+\binom{5}{4} p^{4}(1-p)+p^{5}
\binom{3}{2} p^{2}(1-p)+p^{3}
10 p^{3}(1-p)^{2}+5 p^{4}(1-p)+p^{5}>3 p^{2}(1-p)+p^{3}
3(p-1)^{2}(2 p-1)>0
p>\frac{1}{2}
(b) 일반적으로, $2 k+1$개의 구성 요소를 가진 시스템은 $2 k-1$개의 구성 요소를 가진 시스템보다 $p>\frac{1}{2}$일 때 (그리고 그 경우에만) 더 낫다. 이를 증명하기 위해, $2 k+1$개의 구성 요소를 가진 시스템을 고려하고, 처음 $2 k-1$개 중 작동하는 구성 요소의 수를 $X$라고 하자. 그러면\begin{aligned} P_{2 k+1}(\text { effective })= & P{X \geq k+1}+P{X=k}\left(1-(1-p)^{2}\right) \ & +P{X=k-1} p^{2} \end{aligned}
이는 ( $2 k+1$ )-component 시스템이 다음 중 하나에 해당할 경우 효과적이기 때문이다. (i) $X \geq k+1$; (ii) $X=k$이고 나머지 2개의 구성 요소 중 적어도 하나가 작동하는 경우; 또는 (iii) $X=k-1$이고 다음 2개의 구성 요소가 모두 작동하는 경우. 다음과 같으므로\begin{aligned} P_{2 k-1} \text { (effective) } & =P{X \geq k} \ & =P{X=k}+P{X \geq k+1} \end{aligned}
\begin{aligned} & P_{2 k+1} \text { (effective) }-P_{2 k-1} \text { (effective) } \ & \quad=P{X=k-1} p^{2}-(1-p)^{2} P{X=k} \ & \quad=\binom{2 k-1}{k-1} p^{k-1}(1-p)^{k} p^{2}-(1-p)^{2}\binom{2 k-1}{k} p^{k}(1-p)^{k-1} \ & \quad=\binom{2 k-1}{k} p^{k}(1-p)^{k}[p-(1-p)] \operatorname{since}\binom{2 k-1}{k-1}=\binom{2 k-1}{k} \ & \quad>0 \Leftrightarrow p>\frac{1}{2} \end{aligned}
### 4.6.1 Properties of Binomial Random Variables 이제 매개변수 $n$과 $p$를 갖는 **이항 확률 변수(binomial random variable)**의 속성을 살펴보겠다. 먼저, 기대값과 분산을 계산해 보자.\begin{aligned} E\left[X^{k}\right] & =\sum_{i=0}^{n} i^{k}\binom{n}{i} p^{i}(1-p)^{n-i} \ & =\sum_{i=1}^{n} i^{k}\binom{n}{i} p^{i}(1-p)^{n-i} \end{aligned}
i\binom{n}{i}=n\binom{n-1}{i-1}
\begin{aligned} E\left[X^{k}\right] & =n p \sum_{i=1}^{n} i^{k-1}\binom{n-1}{i-1} p^{i-1}(1-p)^{n-i} \ & =n p \sum_{j=0}^{n-1}(j+1)^{k-1}\binom{n-1}{j} p^{j}(1-p)^{n-1-j} \quad \begin{array}{l} \text { by letting } \ j=i-1 \end{array} \ & =n p E\left[(Y+1)^{k-1}\right] \end{aligned}
여기서 $Y$는 매개변수 $n-1, p$를 갖는 이항 확률 변수이다. 위 방정식에서 $k=1$로 설정하면 다음을 얻는다.E[X]=n p
즉, 각 시행이 확률 $p$로 성공하는 $n$번의 독립적인 시행에서 발생하는 성공의 기대 횟수는 $n p$와 같다. 위 방정식에서 $k=2$로 설정하고 이항 확률 변수의 기대값에 대한 이전 공식을 사용하면 다음을 얻는다.\begin{aligned} E\left[X^{2}\right] & =n p E[Y+1] \ & =n p[(n-1) p+1] \end{aligned}
$E[X]=n p$이므로 다음을 얻는다.\begin{aligned} \operatorname{Var}(X) & =E\left[X^{2}\right]-(E[X])^{2} \ & =n p[(n-1) p+1]-(n p)^{2} \ & =n p(1-p) \end{aligned}
요약하면, 우리는 다음을 보였다: $X$가 매개변수 $n$과 $p$를 갖는 이항 확률 변수라면,\begin{aligned} E[X] & =n p \ \operatorname{Var}(X) & =n p(1-p) \end{aligned}
다음 명제는 이항 확률 질량 함수가 어떻게 처음에는 증가하고 그 다음에는 감소하는지를 자세히 설명한다. 명제 $X$가 매개변수 $(n, p)$를 갖는 이항 확률 변수이고 $0<p<1$일 때, 6.1 $k$가 0부터 $n$까지 변함에 따라 $P\{X=k\}$는 먼저 단조롭게 증가한 다음 단조롭게 감소하며, $(n+1) p$보다 작거나 같은 가장 큰 정수일 때 가장 큰 값에 도달한다. 증명 우리는 $P\{X=k\} / P\{X=k-1\}$를 고려하고 그것이 1보다 크거나 작은 $k$의 값을 결정함으로써 명제를 증명한다. 이제,\begin{aligned} \frac{P{X=k}}{P{X=k-1}} & =\frac{\frac{n!}{(n-k)!k!} p^{k}(1-p)^{n-k}}{\frac{n!}{(n-k+1)!(k-1)!} p^{k-1}(1-p)^{n-k+1}} \ & =\frac{(n-k+1) p}{k(1-p)} \end{aligned}
 그림 4.6 $p(k)=\binom{10}{k}\left(\frac{1}{2}\right)^{10}$의 그래프. 따라서 $P\{X=k\} \geq P\{X=k-1\}$는 다음의 경우에만 성립한다.(n-k+1) p \geq k(1-p)
k \leq(n+1) p
그리고 명제는 증명된다. 명제 6.1의 예시로, 매개변수 $(10, \frac{1}{2})$를 갖는 이항 확률 변수의 확률 질량 함수 그래프인 그림 4.6을 고려해 보자. 예제 6g 미국 대통령 선거에서, 한 주에서 가장 많은 득표를 얻은 후보는 해당 주에 할당된 총 선거인단 투표수를 받는다. 특정 주의 선거인단 투표수는 해당 주의 인구에 대략 비례한다. 즉, 인구 $n$을 가진 주는 대략 $nc$개의 선거인단 투표수를 갖는다. (실제로는 $nc+2$에 더 가깝다. 왜냐하면 주는 하원의원 수에 따라 선거인단 투표수를 받는데, 이 하원의원 수는 주의 인구에 대략 비례하며, 두 명의 상원의원에 대해 각각 한 표의 선거인단 투표수를 받기 때문이다.) 우리는 박빙의 대통령 선거에서 크기 $n$인 주의 시민의 평균 영향력을 결정해 보자. 여기서 박빙 선거에서의 평균 영향력이라 함은, 크기 $n=2k+1$인 주의 유권자가 다른 $n-1$명의 유권자가 두 후보에게 표를 균등하게 나눌 경우 결정적인 역할을 한다는 것을 의미한다. (여기서는 $n$이 홀수라고 가정하지만, $n$이 짝수인 경우도 상당히 유사하다.) 선거가 박빙이므로, 우리는 다른 $n-1=2k$명의 유권자가 독립적으로 행동하며 두 후보 중 한 명에게 투표할 확률이 동일하다고 가정한다. 따라서 크기 $n=2k+1$인 주의 유권자가 결과에 영향을 미칠 확률은 공정한 동전을 $2k$번 던져 앞면과 뒷면이 같은 횟수로 나올 확률과 같다. 즉,\begin{aligned} & P{\text { 크기 } 2 k+1 \text {인 주의 유권자가 영향을 미칠 확률 }} \ & \qquad \begin{array}{c} 2 k \ k \end{array}\right)\left(\frac{1}{2}\right)^{k}\left(\frac{1}{2}\right)^{k} \ & =\frac{(2 k)!}{k!k!2^{2 k}} \end{aligned}
위 등식을 근사하기 위해, 우리는 **Stirling의 근사(Stirling's approximation)**를 사용한다. 이는 $k$가 클 때 다음을 의미한다.k!\sim k^{k+1 / 2} e^{-k} \sqrt{2 \pi}
여기서 $a_{k} / b_{k}$의 비율이 $k$가 $\infty$에 접근할 때 1에 접근하면 $a_{k} \sim b_{k}$라고 말한다. 따라서 다음이 성립한다.\begin{aligned} & P{\text { 크기 } 2 k+1 \text {인 주의 유권자가 영향을 미칠 확률 }} \ & \qquad \sim \frac{(2 k)^{2 k+1 / 2} e^{-2 k} \sqrt{2 \pi}}{k^{2 k+1} e^{-2 k}(2 \pi) 2^{2 k}}=\frac{1}{\sqrt{k \pi}} \end{aligned}
그러한 유권자(만약 그 또는 그녀가 영향을 미친다면)는 $nc$개의 선거인단 투표수에 영향을 미칠 것이므로, 크기 $n$인 주의 유권자가 영향을 미칠 것으로 예상되는 선거인단 투표수, 즉 유권자의 **평균 영향력(average power)**은 다음과 같이 주어진다.\begin{aligned} \text{평균 영향력} & =n c P{\text { 영향을 미칠 확률 }} \ & \sim \frac{n c}{\sqrt{n \pi / 2}} \ & =c \sqrt{2 n / \pi} \end{aligned}
따라서 크기 $n$인 주의 유권자의 평균 영향력은 $n$의 제곱근에 비례하며, 이는 대통령 선거에서 큰 주의 유권자가 작은 주의 유권자보다 더 많은 영향력을 가진다는 것을 보여준다. ### 4.6.2 Computing the Binomial Distribution Function $X$가 매개변수 ($n, p$)를 갖는 이항분포를 따른다고 가정하자. 이 분포 함수를 계산하는 핵심은 다음과 같다:P{X \leq i}=\sum_{k=0}^{i}\binom{n}{k} p^{k}(1-p)^{n-k} \quad i=0,1, \ldots, n
이는 Proposition 6.1의 증명에서 확립된 $P\{X=k+1\}$과 $P\{X=k\}$ 사이의 다음 관계를 활용하는 것이다:P{X=k+1}=\frac{p}{1-p} \frac{n-k}{k+1} P{X=k}
예제 6h $X$가 매개변수 $n=6, p=.4$를 갖는 이항 확률 변수라고 하자. 그러면 $P\{X=0\}=(.6)^{6}$에서 시작하여 Equation (6.3)을 재귀적으로 적용하면 다음을 얻는다:\begin{aligned} & P{X=0}=(.6)^{6} \approx .0467 \ & P{X=1}=\frac{4}{6} \frac{6}{1} P{X=0} \approx .1866 \ & P{X=2}=\frac{4}{6} \frac{5}{2} P{X=1} \approx .3110 \ & P{X=3}=\frac{4}{6} \frac{4}{3} P{X=2} \approx .2765 \ & P{X=4}=\frac{4}{6} \frac{3}{4} P{X=3} \approx .1382 \ & P{X=5}=\frac{4}{6} \frac{2}{5} P{X=4} \approx .0369 \ & P{X=6}=\frac{4}{6} \frac{1}{6} P{X=5} \approx .0041 \end{aligned}
재귀 (6.3)을 활용하여 이항 분포 함수를 계산하는 컴퓨터 프로그램은 쉽게 작성할 수 있다. $P\{X \leq i\}$를 계산하기 위해 프로그램은 먼저 $P\{X=i\}$를 계산한 다음, 재귀를 사용하여 $P\{X= i-1\}, P\{X=i-2\}$ 등을 순차적으로 계산해야 한다. ## Historical note 성공 확률 $p$를 공통으로 갖는 독립 시행은 스위스 수학자 **자크 베르누이(Jacques Bernoulli, 1654-1705)**에 의해 처음 연구되었다. 그의 조카 니콜라스가 그가 사망한 지 8년 후인 1713년에 출판한 저서 **『추측술(Ars Conjectandi)』**에서 베르누이는 이러한 시행의 횟수가 많을 경우, 성공한 시행의 비율이 1에 가까운 확률로 $p$에 근접할 것이라는 것을 보여주었다. 자크 베르누이는 역사상 가장 유명한 수학자 가문의 1세대에 속한다. 총 8명에서 12명에 이르는 베르누이 가문 사람들은 3세대에 걸쳐 확률, 통계 및 수학에 근본적인 공헌을 했다. 정확한 수를 알기 어려운 한 가지 이유는 여러 명이 같은 이름을 가졌다는 사실 때문이다. (예를 들어, 자크의 형제 장(Jean)의 두 아들 중 한 명은 자크, 다른 한 명은 장이라는 이름을 가졌다.) 또 다른 어려움은 여러 베르누이 가문 사람들이 다른 장소에서 다른 이름으로 알려졌다는 점이다. 우리의 자크(때로는 Jaques로 표기)는 예를 들어 **야코프(Jakob, 때로는 Jacob으로 표기)**와 **제임스 베르누이(James Bernoulli)**로도 알려졌다. 그러나 그들의 수가 얼마였든 간에, 그들의 영향력과 업적은 엄청났다. 음악계의 바흐 가문처럼, 수학계의 베르누이 가문은 시대를 초월한 가문이었다! ## Example 6i $X$가 매개변수 $n=100$, $p=.75$를 갖는 이항 확률 변수일 때, $P\{X=70\}$과 $P\{X \leq 70\}$을 구하시오. 풀이 이항 계산기를 사용하여 다음 해를 얻을 수 있다:  그림 4.7