Zaheer, Manzil, et al. "Big bird: Transformers for longer sequences." Advances in neural information processing systems 33 (2020): 17283-17297.

Big Bird: Transformers for Longer Sequences

Manzil Zaheer, Guru Guruganesh, Avinava Dubey, Joshua Ainslie, Chris Alberti, Santiago Ontanon, Philip Pham, Anirudh Ravula, Qifan Wang, Li Yang, Amr Ahmed<br>Google Research<br>{manzilz, gurug, avinavadubey}@google.com

Abstract

BERT와 같은 Transformer 기반 모델은 NLP 분야에서 가장 성공적인 딥러닝 모델 중 하나였다. 하지만 이들의 핵심적인 한계점 중 하나는 **full attention 메커니즘으로 인해 시퀀스 길이에 대해 이차적인 의존성(주로 메모리 측면에서)**을 가진다는 것이다.
이러한 문제를 해결하기 위해 우리는 BigBird라는 sparse attention 메커니즘을 제안한다. 이 메커니즘은 이차적인 의존성을 선형으로 줄여준다.
우리는 BigBird가 시퀀스 함수의 universal approximator이며 Turing complete하다는 것을 증명한다. 이를 통해 이차적인 full attention 모델의 이러한 속성들을 보존한다.
이 과정에서 우리의 이론적 분석은 sparse attention 메커니즘의 일부로서 전체 시퀀스를 attend하는 $O(1)$ 개의 global token (예: CLS 토큰)을 가지는 것의 이점을 밝혀낸다.
제안된 sparse attention은 이전에는 유사한 하드웨어로 가능했던 시퀀스 길이의 최대 8배까지 처리할 수 있다. 더 긴 context를 처리할 수 있는 능력 덕분에, BigBird는 질문 응답 및 요약과 같은 다양한 NLP task에서 성능을 크게 향상시킨다. 우리는 또한 유전체학(genomics) 데이터에 대한 새로운 응용 분야도 제안한다.

1 Introduction

Transformer [91] 기반 모델(예: BERT [22, 63])은 다양한 자연어 처리(NLP) task에서 엄청난 성공을 거두었으며, 그 결과 현대 NLP 연구의 주류가 되었다. 이러한 Transformer의 다재다능함과 견고함이 광범위한 채택의 주요 원동력이다. 이 모델은 다양한 시퀀스 기반 task에 쉽게 적용될 수 있다. 예를 들어, 번역 [91], 요약 [66], 생성 [15] 등을 위한 seq2seq 모델로 사용되거나, 감성 분석 [83], 품사 태깅(POS tagging) [65], 기계 독해(machine reading comprehension) [93] 등을 위한 독립형 encoder로 사용될 수 있으며, LSTM [37]과 같은 이전 시퀀스 모델들을 훨씬 능가하는 것으로 알려져 있다.

Transformer의 핵심 혁신은 self-attention 메커니즘의 도입이다. 이 메커니즘은 입력 시퀀스의 각 토큰에 대해 병렬적으로 평가될 수 있어, LSTM과 같은 recurrent neural network의 순차적 종속성을 제거한다. 이러한 병렬 처리 능력 덕분에 Transformer는 GPU/TPU와 같은 최신 SIMD 하드웨어 가속기의 모든 성능을 활용할 수 있으며, 이는 전례 없는 규모의 데이터셋으로 NLP 모델을 학습시키는 것을 가능하게 한다. 대규모 데이터 학습 능력은 BERT [22] 및 T5 [75]와 같은 모델의 출현으로 이어졌는데, 이 모델들은 대규모 범용 코퍼스에서 Transformer를 사전학습하고 그 지식을 다운스트림 task로 전이시킨다. 이러한 사전학습은 데이터가 부족한 다운스트림 task [51]뿐만 아니라 충분한 데이터가 있는 task [101]에서도 상당한 성능 향상을 가져왔으며, 따라서 현대 NLP에서 Transformer가 널리 사용되는 주요 원동력이 되었다.

self-attention 메커니즘은 입력 시퀀스의 각 토큰이 시퀀스 내의 다른 모든 토큰에 독립적으로 attend할 수 있도록 함으로써 RNN의 제약(즉, RNN의 순차적 특성)을 극복한다. 이러한 설계 선택은 몇 가지 흥미로운 결과를 낳는다. 특히, full self-attention은 시퀀스 길이에 대해 제곱에 비례하는 계산 및 메모리 요구 사항을 가진다. 코퍼스는 클 수 있지만, 많은 애플리케이션에서 context를 제공하는 시퀀스 길이는 매우 제한적이라는 점에 주목해야 한다. 현재 일반적으로 사용 가능한 하드웨어 및 모델 크기를 고려할 때, 이러한 요구 사항은 대략 512 토큰 길이의 입력 시퀀스를 처리할 수 있는 수준으로 해석된다. 이는 QA [60], 문서 분류 등 더 큰 context를 요구하는 task에 대한 직접적인 적용 가능성을 감소시킨다.

그러나 self-attention과 Transformer가 유용하다는 것을 알고 있지만, 우리의 이론적 이해는 아직 초보적인 수준이다. self-attention 모델의 어떤 측면이 성능에 필수적인가? Transformer 및 유사 모델의 표현력(expressivity)에 대해 무엇을 말할 수 있는가? 애초에 제안된 self-attention 메커니즘이 RNN만큼 효과적인지조차 설계만으로는 명확하지 않았다. 예를 들어, self-attention은 permutation equivariant하기 때문에 시퀀스 순서를 따르지 않는다. 이러한 우려는 부분적으로 해결되었는데, Yun et al. [104]은 Transformer가 compact domain을 가진 모든 연속적인 sequence-to-sequence 함수를 포착할 만큼 충분히 표현력이 있다는 것을 보여주었다. 한편, Pérez et al. [72]은 **full Transformer가 Turing Complete하다(즉, 완전한 튜링 머신을 시뮬레이션할 수 있다)**는 것을 보여주었다. 여기서 두 가지 자연스러운 질문이 제기된다: 더 적은 내적(inner-product)을 사용하여 완전히 제곱에 비례하는 self-attention 방식의 경험적 이점을 달성할 수 있는가? 이러한 sparse attention 메커니즘이 원래 네트워크의 표현력과 유연성을 유지하는가?

본 논문에서는 위 두 질문에 모두 답하고, 긴 context를 요구하는 다양한 task에서 성능을 향상시키는 sparse attention 메커니즘을 제시한다. 우리는 BigBird를 체계적으로 개발했으며, 이는 토큰 수에 대해 선형적인 복잡도를 가지는 attention 메커니즘이다 (Sec. 2). 우리는 그래프 희소화(graph sparsification) 방법에서 영감을 얻었으며, full-attention이 제안된 attention 패턴으로 완화될 때 Transformer의 표현력 증명이 어디에서 무너지는지를 이해했다. 이러한 이해는 이론적으로도 표현력이 뛰어나고 경험적으로도 유용한 BigBird를 개발하는 데 도움이 되었다. 특히, 우리의 BIGBIRD는 세 가지 주요 부분으로 구성된다:

• 시퀀스의 모든 부분에 attend하는 $g$개의 global token 집합.
• $w$개의 인접한 local token 집합에 attend하는 모든 토큰.
• $r$개의 random token 집합에 attend하는 모든 토큰.

이는 훨씬 더 긴 시퀀스 길이(8배)까지 확장 가능한 고성능 attention 메커니즘으로 이어진다. 요약하자면, 우리의 주요 기여는 다음과 같다:

1. BigBird는 full Transformer의 알려진 모든 이론적 속성을 만족한다 (Sec. 3). 특히, 우리는 추가 토큰을 추가함으로써 $O(n)$개의 내적만으로 모든 연속적인 sequence-to-sequence 함수를 표현할 수 있음을 보여준다. 또한, 정밀도에 대한 표준 가정 하에 BigBird가 Turing complete함을 보여준다.
2. 경험적으로, 우리는 BigBird가 모델링하는 확장된 context가 다양한 NLP task에 이점을 제공함을 보여준다. 우리는 질문 응답 및 문서 요약 task에서 여러 데이터셋에 걸쳐 state-of-the-art 결과를 달성한다. 이러한 결과의 요약은 Sec. 4에 제시되어 있다.
3. 마지막으로, 우리는 긴 context가 유익한 attention 기반 모델의 새로운 응용 분야를 소개한다: DNA와 같은 유전체 시퀀스의 contextual representation 추출. 더 긴 masked LM 사전학습을 통해, BigBird는 promoter-region 및 chromatin profile 예측과 같은 다운스트림 task에서 성능을 향상시킨다 (Sec. 5).

1.1 Related Work

Transformer의 quadratic dependency를 완화하기 위한 흥미로운 시도들이 많이 있었으며, 이는 크게 두 가지 방향으로 분류할 수 있다.

첫 번째 연구 방향은 길이 제한을 수용하고 그 안에서 방법을 개발하는 것이다. 이 범주의 가장 간단한 방법은 단순히 sliding window를 사용하는 것이지만 [93], 일반적으로 대부분의 연구는 다음의 일반적인 패러다임에 속한다: 다른 메커니즘을 사용하여 Transformer에 입력할 관련 context의 더 작은 subset을 선택하고, 선택적으로 반복하여 매번 다른 context로 Transformer 블록을 여러 번 호출하는 방식이다. 가장 대표적으로 SpanBERT [42], ORQA [54], REALM [34], RAG [57]는 다양한 task에서 강력한 성능을 달성했다. 그러나 이러한 방법들은 종종 상당한 엔지니어링 노력(예: 대규모 nearest neighbor 검색을 통한 역전파)을 요구하며 학습하기 어렵다는 점에 주목할 필요가 있다.

두 번째 연구 방향은 full attention이 필수적인지에 대한 의문을 제기하고, full attention을 요구하지 않으면서 메모리 및 계산 요구 사항을 줄이는 접근 방식을 시도했다. 대표적으로 Dai et al. [21], Sukhbaatar et al. [82], Rae et al. [74]는 left-to-right language modeling에는 잘 작동하지만, bidirectional context를 요구하는 task에서는 어려움을 겪는 auto-regressive 모델을 제안했다. Child et al. [16]은 복잡도를 $O(n \sqrt{n})$으로 줄이는 sparse 모델을 제안했으며, Kitaev et al. [49]는 LSH를 사용하여 nearest neighbor를 계산함으로써 복잡도를 $O(n \log (n))$으로 더욱 줄였다.

Figure 1: BIGBIRD에 사용된 attention 메커니즘의 구성 요소. 흰색은 attention이 없음을 나타낸다. (a) $r=2$인 random attention, (b) $w=3$인 sliding window attention, (c) $g=2$인 global attention, (d) 결합된 BigBird 모델.

Ye et al. [103]은 데이터의 binary partition을 제안했으며, Qiu et al. [73]은 block sparsity를 사용하여 복잡도를 줄였다. 최근 Longformer [8]는 계산을 줄이고 BERT를 더 긴 시퀀스 기반 task로 확장하기 위해 몇 개의 global mask와 함께 localized sliding window 기반 mask를 도입했다. 마지막으로, 우리의 연구는 Extended Transformers Construction [4]의 연구와 밀접하게 관련되어 있으며 이를 기반으로 한다. 이 연구는 Transformer를 위한 텍스트의 구조를 인코딩하도록 설계되었다. Global token의 아이디어는 그들의 목표를 달성하기 위해 광범위하게 사용되었다. 우리의 이론적 연구는 이러한 모델의 성공에 대한 정당성을 제공하는 것으로도 볼 수 있다. 언급된 대부분의 방법은 휴리스틱 기반이며 경험적으로 원래의 Transformer만큼 다재다능하고 견고하지 않다, 즉 동일한 아키텍처가 여러 표준 벤치마크에서 SoTA를 달성하지 못한다는 점에 유의하는 것이 중요하다. (우리의 모든 비교에 포함된 Longformer는 한 가지 예외이다. 더 자세한 비교는 App. E. 3 참조). 또한, 이러한 근사치들은 이론적인 보장을 제공하지 않는다.

2 BigBird Architecture

이 섹션에서는 입력 시퀀스 $\boldsymbol{X}=\left(\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{n}\right) \in \mathbb{R}^{n \times d}$에 대해 작동하는 Transformer의 각 layer에서 사용되는 일반화된 attention mechanism을 갖춘 BigBird 모델에 대해 설명한다.
일반화된 attention mechanism은 정점 집합이 $[n]= \{1, \ldots, n\}$인 방향 그래프 $D$로 설명된다. 호(방향성 있는 엣지)의 집합은 attention mechanism이 고려할 내적(inner product)의 집합을 나타낸다.
$N(i)$를 $D$에서 노드 $i$의 out-neighbors 집합이라고 할 때, 일반화된 attention mechanism의 $i^{\text {th }}$ 출력 벡터는 다음과 같이 정의된다:

$$\operatorname{ATTN}_{D}(\boldsymbol{X})_{i}=\boldsymbol{x}_{i}+\sum_{h=1}^{H} \sigma\left(Q_{h}\left(\boldsymbol{x}_{i}\right) K_{h}\left(\boldsymbol{X}_{N(i)}\right)^{T}\right) \cdot V_{h}\left(\boldsymbol{X}_{N(i)}\right)$$

여기서 $Q_{h}, K_{h}: \mathbb{R}^{d} \rightarrow \mathbb{R}^{m}$는 각각 query 및 key 함수이고, $V_{h}: \mathbb{R}^{d} \rightarrow \mathbb{R}^{d}$는 value 함수이며, $\sigma$는 scoring 함수(예: softmax 또는 hardmax)이고, $H$는 head의 수를 나타낸다. 또한, $X_{N(i)}$는 모든 입력이 아닌 $\left\{\boldsymbol{x}_{j}: j \in N(i)\right\}$만을 쌓아서 형성된 행렬에 해당한다.
만약 $D$가 완전 방향 그래프(complete digraph)라면, 우리는 Vaswani et al. [91]의 완전한 quadratic attention mechanism을 얻게 된다.
설명을 단순화하기 위해, 우리는 기본 그래프가 sparse하더라도 그래프 $D$의 인접 행렬 $A$를 사용하여 설명할 것이다.
자세히 설명하자면, $A \in[0,1]^{n \times n}$는 query $i$가 key $j$에 attend하면 $A(i, j)=1$이고, 그렇지 않으면 0이다. 예를 들어, $A$가 모든 원소가 1인 행렬(BERT에서와 같이)일 경우, 모든 토큰이 다른 모든 토큰에 attend하므로 quadratic complexity를 초래한다.
self-attention을 완전 연결 그래프로 보는 이러한 관점은 기존 그래프 이론을 활용하여 복잡도를 줄이는 데 도움이 된다. self-attention의 quadratic complexity를 줄이는 문제는 이제 그래프 희소화(graph sparsification) 문제로 볼 수 있다.
랜덤 그래프는 expander이며, 스펙트럼 특성 [80, 38]을 포함한 여러 다른 맥락에서 완전 그래프를 근사할 수 있음이 잘 알려져 있다. 우리는 attention mechanism을 위한 sparse random graph가 두 가지 바람직한 특성을 가져야 한다고 생각한다: **노드 간의 작은 평균 경로 길이(average path length)**와 지역성(locality) 개념이다. 각각에 대해 아래에서 논의한다.
Erdős-Rényi 모델로 알려진 가장 간단한 랜덤 그래프 구성을 고려해보자. 이 모델에서는 각 엣지가 고정된 확률로 독립적으로 선택된다. 단 $\tilde{\Theta}(n)$개의 엣지만을 가진 이러한 랜덤 그래프에서, 임의의 두 노드 사이의 최단 경로는 노드 수에 대해 로그적이다 [17, 43]. 결과적으로, 이러한 랜덤 그래프는 완전 그래프를 스펙트럼적으로 근사하며, 두 번째 고유값(인접 행렬의)이 첫 번째 고유값과 상당히 떨어져 있다 [9, 10, 6]. 이 속성은 그래프 내 랜덤 워크의 빠른 혼합 시간(mixing time)으로 이어지며, 이는 비공식적으로 어떤 노드 쌍 사이에서도 정보가 빠르게 흐를 수 있음을 시사한다. 따라서 우리는 각 query가 $r$개의 랜덤한 key에 attend하는 sparse attention을 제안한다. 즉, $A(i, \cdot)=1$은 $r$개의 무작위로 선택된 key에 해당한다 (Fig. 1a 참조).

BIGBIRD 생성에 영감을 준 두 번째 관점은 NLP 및 계산 생물학 분야의 대부분의 맥락에서 데이터가 상당한 참조 지역성(locality of reference)을 나타낸다는 것이다. 이 현상에서는 토큰에 대한 많은 정보가 인접 토큰으로부터 파생될 수 있다. 특히 Clark et al. [19]은 NLP task에서 self-attention 모델을 조사하고 인접한 내적(inner-product)이 매우 중요하다고 결론지었다. 언어 구조에서 토큰의 근접성(proximity)인 지역성 개념은 **변형-생성 문법(transformational-generative grammar)**과 같은 다양한 언어 이론의 기초를 형성하기도 한다.
그래프 이론 용어에서 클러스터링 계수(clustering coefficient)는 연결성의 지역성을 측정하는 척도이며, 그래프에 많은 clique 또는 near-clique(거의 완전히 상호 연결된 서브그래프)가 포함될 때 높다. 단순한 Erdős-Rényi 랜덤 그래프는 높은 클러스터링 계수를 가지지 않지만 [84], small world graph로 알려진 랜덤 그래프 클래스는 높은 클러스터링 계수를 나타낸다 [94]. Watts와 Strogatz [94]가 도입한 특정 모델은 평균 최단 경로와 지역성 개념 사이의 좋은 균형을 달성하므로 우리에게 매우 중요하다. 그들의 모델의 생성 과정은 다음과 같다: 정규 링 격자(regular ring lattice)를 구성한다. 이는 각 노드가 $w$개의 이웃(각 측면에 $w/2$개)에 연결된 $n$개의 노드를 가진 그래프이다.
다시 말해, 우리는 노드에 대한 슬라이딩 윈도우로 시작한다. 그런 다음 모든 연결의 무작위 부분 집합($k \%$)이 무작위 연결로 대체된다. 나머지 $(100-k) \%$의 로컬 연결은 유지된다. 그러나 이러한 무작위 엣지를 삭제하는 것은 최신 하드웨어에서 비효율적일 수 있으므로, 우리는 이를 유지하며, 이는 그 속성에 영향을 미치지 않을 것이다. 요약하자면, BigBird에서는 이러한 문맥 내의 로컬 구조를 포착하기 위해 슬라이딩 윈도우 attention을 정의한다. 따라서 너비 $w$의 self-attention 동안, 위치 $i$의 query는 $i-w/2$부터 $i+w/2$까지의 key에 attend한다. 우리의 표기법으로는 $A(i, i-w/2: i+w/2)=1$이다 (Fig. 1b 참조).
초기적인 건전성 검사로, 우리는 이러한 직관이 BERT와 유사한 모델에 가까운 성능을 얻는 데 충분한지, 동시에 attention을 토큰 수에 대해 선형으로 유지하는지 테스트하기 위한 기본 실험을 수행했다. 우리는 랜덤 블록과 로컬 윈도우만으로는 BERT의 성능과 경쟁하는 데 필요한 모든 문맥을 포착하기에 불충분하다는 것을 발견했다.

Table 1: Building block comparison @512

BIGBIRD의 마지막 부분은 우리의 이론적 분석(Sec. 3)에서 영감을 받았으며, 이는 경험적 성능에 매우 중요하다. 더 구체적으로, 우리의 이론은 "global token"의 중요성을 활용한다 (시퀀스의 모든 토큰에 attend하고, 모든 토큰이 attend하는 토큰 (Fig. 1c 참조)). 이러한 global token은 두 가지 방식으로 정의될 수 있다:

• BIGBIRD-ITC: **Internal Transformer Construction (ITC)**에서는 일부 기존 토큰을 "global"로 만들어 전체 시퀀스에 attend하게 한다. 구체적으로, 우리는 인덱스 집합 $G$ (여기서 $g:=|G|$)를 선택하여, 모든 $i \in G$에 대해 $A(i,:)=1$ 및 $A(:, i)=1$이 되도록 한다.
• BigBird-ETC: **Extended Transformer Construction (ETC)**에서는 CLS와 같은 추가적인 "global" 토큰을 포함한다. 구체적으로, 우리는 기존의 모든 토큰에 attend하는 $g$개의 global token을 추가한다. 우리의 표기법으로는, 이는 행렬 $A$에 $g$개의 행을 추가하여 새로운 행렬 $B \in[0,1]^{(N+g) \times(N+g)}$를 생성하는 것에 해당한다. 이때 모든 $i \in\{1,2, \ldots g\}$에 대해 $B(i,:)=1$ 및 $B(:, i)=1$이 되고, 모든 $i, j \in\{1, \ldots, N\}$에 대해 $B(g+i, g+j)=A(i, j)$가 된다. 이는 문맥을 저장할 추가적인 위치를 제공하며, 실험에서 보듯이 성능을 향상시킨다.

BigBird의 최종 attention mechanism (Fig. 1d)은 이 세 가지 속성을 모두 가진다: query는 $r$개의 랜덤 key에 attend하고, 각 query는 자신의 위치에서 왼쪽으로 $w/2$개, 오른쪽으로 $w/2$개의 토큰에 attend하며, $g$개의 global token을 포함한다 (global token은 기존 토큰이거나 추가된 토큰일 수 있다). 구현 세부 사항은 App. D에 제공된다.

3 Theoretical Results about Sparse Attention Mechanism

이 섹션에서는 sparse attention mechanism이 full-attention mechanism만큼 강력하고 표현력이 풍부하다는 것을 두 가지 측면에서 보여줄 것이다.
첫째, sparse attention mechanism이 **독립형 encoder (예: BERT)**에 사용될 때, Yun et al. [104]의 방식과 같이 sequence-to-sequence 함수의 Universal Approximator임을 보인다. 이 속성은 동시대 연구인 Yun et al. [105]에서도 이론적으로 탐구되었다.
둘째, [105]와 달리, 우리는 sparse encoder-decoder Transformer가 Turing Complete임을 추가로 보인다 ([72]에 정의된 동일한 조건을 가정).
위의 긍정적인 결과들을 보완하여, 우리는 sparse-attention mechanism으로 전환하는 데 비용이 발생한다는 것, 즉 **공짜 점심은 없다(no free lunch)**는 것을 또한 보여준다. Section 3.4에서는 충분히 sparse한 mechanism이 다항식적으로 더 많은 layer를 필요로 하는 자연스러운 task를 제시함으로써 **하한(lower bounds)**을 보인다.

3.1 Notation

완전한 Transformer encoder stack은 단일 layer encoder의 반복적인 적용으로 구성된다 (각 layer는 독립적인 파라미터를 가짐). 우리는 일반화된 encoder (Sec. 2)를 사용하여 정의된 이러한 Transformer encoder stack의 클래스를 $\mathcal{T}_{D}^{H, m, q}$로 표기한다. 여기서 $H$는 head의 개수, $m$은 head size, $q$는 출력 네트워크의 hidden layer size를 나타내며, attention layer는 directed graph $D$에 의해 정의된다.

우리가 제안하는 attention mechanism과 Vaswani et al. [91], Yun et al. [104]의 방식 간의 주요 차이점은, 우리는 각 시퀀스의 시작 부분에 특별한 token을 추가하고 이에 특별한 벡터를 할당한다는 점이다. 우리는 이를 $\boldsymbol{x}_{0}$라고 부를 것이다. 따라서 우리의 그래프 $D$는 vertex set $\{0\} \cup[n]=\{0,1,2, \ldots, n\}$을 가질 것이다. 우리는 이 추가 노드와 해당 벡터가 Transformer의 최종 출력 layer에서 제거될 것이라고 가정한다. 번거로운 표기법을 피하기 위해, 우리는 여전히 Transformer를 시퀀스 $\boldsymbol{X} \in \mathbb{R}^{n \times d}$를 $\mathbb{R}^{n \times d}$로 매핑하는 것으로 취급할 것이다. 또한 우리는 Transformer가 입력 layer에서 행렬 $X$에 position embedding $E \in \mathbb{R}^{d \times n}$을 추가할 수 있도록 허용할 것이다.

마지막으로, universal approximation property를 증명하기 위해 함수 클래스와 거리 측정(distance measure)을 정의해야 한다. $\mathcal{F}_{C D}$는 $\ell_{p}$ norm으로 정의된 토폴로지에 대해 연속적인 함수 $f:[0,1]^{n \times d} \rightarrow \mathbb{R}^{n \times d}$의 집합을 나타낸다. 모든 $p \geq 1$에 대해 $\ell_{p}$ 거리는 $d_{p}\left(f_{1}, f_{2}\right)= \left(\int\left\|f_{1}(X)-f_{2}(X)\right\|_{p}^{p} d X\right)^{1 / p}$임을 상기하라.

3.2 Universal Approximators

정의 1. 0을 중심으로 하는 **스타 그래프(star-graph) $S$**는 $\{0, \ldots, n\}$에 정의된 그래프이다. 모든 정점 $i \in \{1, \ldots, n\}$의 이웃은 $N(i)=\{0, i\}$이고, $N(0)=\{1, \ldots n\}$이다.

우리의 주요 정리는 $S$를 포함하는 모든 그래프에 의해 정의된 sparse attention 메커니즘이 universal approximator라는 것이다:

정리 1. $1<p<\infty$이고 $\epsilon>0$이 주어졌을 때, 임의의 $f \in \mathcal{F}_{C D}$에 대해, sparse-attention을 가진 Transformer $g \in \mathcal{T}_{D}^{H, m, q}$가 존재하여 $d_{p}(f, g) \leq \epsilon$을 만족한다. 여기서 $D$는 스타 그래프 $S$를 포함하는 임의의 그래프이다.

이 정리를 증명하기 위해, 우리는 [104]에 제시된 표준 증명 구조를 따를 것이다.

단계 1: $\mathcal{F}_{C D}$를 piece-wise constant 함수로 근사.
$f$는 유계 도메인 $[0,1)^{n \times d}$를 가진 연속 함수이므로, 우리는 이를 적절한 piece-wise constant 함수로 근사할 것이다. 이는 영역 $[0,1)$를 세분화 $\delta$의 그리드로 적절히 분할하여 **이산 집합 $\mathbb{G}_{\delta}$**를 얻음으로써 달성된다. 따라서 우리는 $d_{p}(f, \bar{f}) \leq \frac{\epsilon}{3}$를 만족하는 함수 $\bar{f}: \mathbb{G}_{\delta} \rightarrow \mathbb{R}^{n \times d}$를 다루고 있다고 가정할 수 있다.

단계 2: piece-wise constant 함수를 수정된 Transformer로 근사.
이것은 증명의 핵심 단계로, self-attention 메커니즘이 입력의 contextual-mapping을 생성하는 데 사용된다. 비공식적으로, contextual mapping은 행렬 $(\boldsymbol{X}, \boldsymbol{x}_{i})$과 열로 구성된 쌍에 대한 고유한 코드이다. 이 고유성은 Feed forward layer가 각 코드를 사용하여 고유한 출력 열로 매핑할 수 있도록 한다.
주요 기술적 과제는 sparse attention 메커니즘만을 사용하여 contextual mapping을 계산하는 것이다. 이는 [104]에서 특정 구간에 있는 항목을 위로 이동시키는 "선택적(selective) shift operator"를 사용하여 수행되었다. 그들의 증명에서 핵심은 shift가 가장 큰 항목에서 가장 작은 항목까지의 범위와 정확히 일치한다는 사실이었다.

sparse attention 메커니즘으로 contextual mapping을 생성하는 것은 상당히 어려운 일이다. 특히, 각 query가 소수의 key에만 attend하기 때문에, 전체 행렬의 contextual embedding을 만들기 위해 충분한 정보를 모을 수 있을지는 전혀 명확하지 않다. 이를 해결하기 위해, 우리는 특정 범위 내에 있는 행렬의 항목들을 이동시키는 sparse shift operator를 개발한다. shift의 정확한 양은 directed sparse attention graph $D$에 의해 제어된다. 두 번째 핵심 요소는 추가적인 global token의 사용이다. 이 operator를 선택된 범위 집합에 신중하게 적용함으로써, 우리는 각 열이 전체 매핑의 고유한 매핑을 포함할 것임을 보일 것이다. 따라서 우리는 여러 layer와 보조 global token을 사용하여 self attention 메커니즘의 내적 손실을 보강할 수 있다.

단계 3: 수정된 Transformer를 원래 Transformer로 근사.
마지막 단계는 수정된 Transformer를 ReLU와 softmax를 사용하는 원래 Transformer로 근사하는 것이다.
전체 세부 사항은 App.A에 제공된다.

3.3 Turing Completeness

Transformer는 매우 범용적인 클래스이다. Vaswani et al. [91]의 원 논문에서는 encoder와 decoder 모두에 Transformer가 사용되었다. 이전 섹션에서 encoder만으로도 얼마나 강력한지를 설명했지만, decoder와 encoder를 함께 사용하는 것이 어떤 추가적인 능력을 제공하는지는 또 다른 자연스러운 질문이다. Pérez et al. [72]은 quadratic attention mechanism에 기반한 full Transformer가 Turing Complete함을 보였다. 이 결과는 모델이 임의 정밀도(arbitrary precision)로 작동한다는 비현실적인 가정을 전제로 한다. 물론, 이 가정이 없으면 Transformer는 유한 상태 기계(finite state machine)로 제한되어 Turing Complete할 수 없으므로 필수적이다.

full attention mechanism이 필수적인지에 대한 질문은 자연스럽다. 즉, sparse attention mechanism으로도 모든 Turing Machine을 시뮬레이션할 수 있는가? 우리는 이것이 실제로 가능함을 보인다: sparse encoder와 sparse decoder를 사용하여 모든 Turing Machine을 시뮬레이션할 수 있다.

Transformer 아키텍처에서 sparse attention mechanism을 사용하려면, 각 토큰이 이전 토큰에만 반응하도록 적절한 수정이 필요하다. BERT의 경우 전체 attention mechanism이 한 번에 적용되지만, full Transformer에서는 decoder 측의 sparse attention mechanism이 토큰별로 사용된다. 둘째, Pérez et al. [72]의 연구는 각 토큰을 테이프 기록(tape history)의 표현으로 사용하고, full attention을 사용하여 올바른 테이프 심볼을 이동하고 검색한다. Pérez et al. [72]의 대부분의 구성은 sparse attention에도 적용되지만, 과거를 가리키는 주소 지정 방식(addressing scheme) ([72]의 Lemma B.4)은 예외이다. 우리는 sparse attention mechanism을 사용하여 이를 시뮬레이션하는 방법을 보여주며, 자세한 내용은 App.B에 기술한다.

3.4 Limitations

우리는 $O(1)$ layer의 full attention 메커니즘으로 해결할 수 있는 자연스러운 task를 제시한다. 그러나 표준 복잡도 이론적 가정 하에서는, 이 문제는 $\tilde{O}(n)$개의 엣지를 가진 모든 sparse attention layer(BIGBIRD뿐만 아니라)에 대해 $\tilde{\Omega}(n)$ layer를 요구한다. (여기서 $\tilde{O}$는 poly-logarithmic factor를 숨긴다.)
주어진 길이 $n$의 시퀀스에서 각 벡터에 대해 가장 멀리 떨어진(furthest) 벡터를 찾는 간단한 문제를 고려해보자. 공식적으로는 다음과 같다:

Task 1. $n$개의 단위 벡터 $\left\{u_{1}, \ldots, u_{n}\right\}$가 주어졌을 때, $f\left(u_{1}, \ldots, u_{n}\right) \rightarrow\left(u_{1 *}, \ldots, u_{n^{*}}\right)$를 찾는다. 여기서 고정된 $j \in[n]$에 대해 $j^{*}=\arg \max _{k}\left\|u_{k}-u_{j}\right\|_{2}^{2}$로 정의된다.

단위 벡터의 경우, 가장 멀리 떨어진 벡터를 찾는 것은 내적(inner product)을 최소화하는 문제로 귀결된다. 적절한 query와 key를 가진 full-attention 메커니즘의 경우, 모든 쌍별 내적을 평가할 수 있으므로 이 task는 매우 쉽다.

Sparse-attention에 대한 불가능성은 Orthogonal Vector Conjecture (OVC) [1, 2, 7, 96]에서 비롯된 **난이도 결과(hardness results)**에서 기인한다. OVC는 fine-grained complexity에서 널리 사용되는 가정이다. 비공식적으로, OVC는 $n$개의 boolean 벡터들 사이에서 최소 내적이 0인지 여부를 subquadratic 시간 내에 결정할 수 없다고 명시한다.
Appendix C에서 우리는 OVC를 사용하여, $\tilde{O}(n)$개의 엣지(즉, 내적 평가)를 가진 sparse directed graph $D$에 대한 Transformer $g \in \mathcal{T}_{D}^{H=1, m=2 d, q=0}$가 Task 1을 평가할 수 있다면, orthogonal vector problem을 해결할 수 있음을 보여주는 환원(reduction)을 제시한다.

Proposition 1. Task 1을 평가할 수 있는 단일 layer full self-attention $g \in \mathcal{T}^{H=1, m=2 d, q=0}$가 존재한다. 즉, $g\left(u_{1}, \ldots, u_{n}\right)=\left[u_{1 *}, \ldots, u_{n^{*}}\right]$이다. 그러나 $\tilde{O}(n)$개의 엣지(즉, 내적 평가)를 가진 모든 sparse-attention graph $D$에 대해서는 $\tilde{\Omega}\left(n^{1-o(1)}\right)$ layer가 필요할 것이다.

이 사실에 대한 공식적인 증명은 Appendix C에 제시되어 있다.

4 Experiments: Natural Language Processing

이 섹션에서는 NLP task를 위해 더 긴 입력 시퀀스를 모델링하는 것의 이점을 보여주는 것을 목표로 하며, 이를 위해 세 가지 대표적인 task를 선정한다.
먼저, **기본적인 Masked Language Modeling (MLM; Devlin et al. 22)**을 통해 더 긴 연속적인 시퀀스를 활용하여 더 나은 contextual representation을 학습할 수 있는지 확인한다.
다음으로, supporting evidence가 있는 QA task를 고려한다. 이 경우, 더 긴 시퀀스를 처리하는 능력은 TF-IDF/BM25와 같은 기본적인 시스템을 사용하여 더 많은 evidence를 검색할 수 있도록 해줄 것이다.

Table 2: Base size 모델을 사용한 QA Dev 결과. WikiHop은 정확도(accuracy)를, HotpotQA, Natural Questions, TriviaQA는 F1 점수를 보고한다.

Table 3: QA task의 Test set에 대한 Fine-tuning 결과. Test 결과(HotpotQA, Natural Questions, TriviaQA는 F1, WikiHop은 Accuracy)는 각 리더보드에서 가져왔다. 각 task별로 BigBird-etc를 제외한 상위 3개 리더를 선정했다. Natural Questions Long Answer (LA), TriviaQA, WikiHop에서 BigBird-ETC는 새로운 state-of-the-art이다. HotpotQA에서는 F1 기준으로 리더보드 3위, Exact Match (EM) 기준으로 2위이다.

마지막으로, 우리는 정보가 처음 512개 토큰에 위치하지 않을 수 있는 긴 문서 분류(long document classification) task를 다룬다. 아래에서는 시퀀스 길이 $4096^{1}$를 사용한 BIGBIRD의 결과를 요약하며, 계산 자원, 배치 크기, 스텝 크기를 포함한 모든 다른 설정 세부 사항은 App. E로 미룬다.

사전학습 및 MLM
우리는 [22, 63]을 따라 BigBird의 base 및 large 버전을 생성하고 MLM objective를 사용하여 사전학습한다. 이 task는 마스킹된 토큰의 무작위 부분집합을 예측하는 것을 포함한다. 우리는 사전학습을 위해 4개의 표준 데이터셋을 사용하며 (App. E.1, Tab. 97에 나열됨), 공개된 RoBERTa 체크포인트 ${ }^{2}$에서 warm-starting한다. 우리는 [8]을 따라 마스킹된 토큰을 예측하는 성능을 bits per character 단위로 비교한다. App. E.1, Tab. 10에서 볼 수 있듯이, BigBird와 Longformer 모두 제한된 길이의 RoBERTa보다 더 나은 성능을 보이며, BIGBIRD-ETC가 가장 좋은 성능을 보인다. 우리는 모델을 합리적인 16GB 메모리/칩에서 32-64의 배치 크기로 학습시켰다. 우리의 메모리 효율성은 Sec. 2에서 설명된 sparse attention 메커니즘의 효율적인 블로킹 및 희소 구조 덕분이다.

질의응답 (Question Answering, QA)
우리는 다음 네 가지 도전적인 데이터셋을 고려했다:

1. Natural Questions [52]: 주어진 질문에 대해 주어진 evidence에서 짧은 답변(SA)을 찾고, 정답에 대한 정보를 포함하는 단락(LA)을 강조한다.
2. HotpotQA-distractor [100]: Natural Questions와 유사하게, 주어진 evidence에서 multi-hop reasoning에 필요한 답변(Ans)과 supporting facts (Sup)를 다른 문서에 걸쳐 찾아야 한다.
3. TriviaQA-wiki [41]: 주어진 Wikipedia evidence를 사용하여 질문에 대한 답변을 제공해야 하지만, 답변이 주어진 evidence에 없을 수도 있다. 질문의 더 작은 verified subset에서는 주어진 evidence에 답변이 포함되어 있음이 보장된다. 그럼에도 불구하고, 우리는 이 경우에도 답변을 span selection 문제로 모델링한다.
4. WikiHop [95]: 주어진 evidence에 있는 여러 문서에 걸쳐 퍼져 있는 정보를 통합하여 multiple-choice questions (MCQ)에서 올바른 옵션을 선택한다.

이러한 task들은 매우 경쟁이 치열하며, 각 데이터셋의 출력 형식에 맞춰 여러 고도로 엔지니어링된 시스템들이 설계되었다. 공정한 비교를 위해, 우리는 BigBIRD 학습을 위해 일부 추가적인 regularization을 사용해야 했으며, 이에 대한 자세한 내용은 정확한 아키텍처 설명과 함께 App. E.2에 제공된다. 우리는 base size 모델을 사용하여 실험하고 각 데이터셋에 대한 개발 세트에서 최상의 구성을 선택한다 (Tab. 2에 보고됨). 확장된 global token을 가진 BigBird-ETC가 다른 모든 모델보다 지속적으로 우수한 성능을 보임을 알 수 있다. 따라서 우리는 이 구성을 선택하여 숨겨진 테스트 세트 평가에 사용될 large size 모델을 학습시켰다.

Tab. 3에서는 BigBird-ETC 모델을 BigBird를 제외한 리더보드 상위 3개 항목과 비교한다. Longformer와 BigBird 모두 더 작은 context를 가진 모델보다 우수한 성능을 보이므로, 더 긴 context를 사용하는 것의 중요성을 분명히 알 수 있다. 또한, BigBird 제출은 단일 모델인 반면, Natural Questions의 다른 상위 3개 항목은 앙상블 모델이라는 점에 주목할 필요가 있다. 이는 정확한 답변 구문 선택에서 약간 낮은 정확도를 설명할 수 있다.

분류 (Classification)
우리는 다양한 길이와 내용을 가진 데이터셋, 특히 다양한 문서 분류 및 GLUE task에 대해 실험한다. BERT를 따라, 우리는 첫 번째 [CLS] 토큰 위에 cross entropy loss를 가진 하나의 layer를 사용했다. 우리는 문서가 길고 학습 예시가 적을 때 BigBird를 사용하는 이점이 더 중요하다는 것을 확인했다. 예를 들어, base size 모델을 사용하여 BigBird는 Arxiv 데이터셋의 state-of-the-art를 약 5% 포인트 향상시킨다. Patents 데이터셋에서는 단순한 BERT/RoBERTa를 사용하는 것보다 개선이 있었지만, 학습 데이터의 규모가 크기 때문에 SoTA (BERT 기반이 아님)에 대한 개선은 유의미하지 않다. 이 성능 향상은 훨씬 작은 IMDb 데이터셋에서는 나타나지 않는다. 실험 설정 세부 사항과 함께, 우리는 경쟁력 있는 성능을 보여주는 자세한 결과를 App. E.4에 제시한다.

4.1 Encoder-Decoder Tasks

encoder-decoder 구조의 경우, full self attention으로 인해 quadratic complexity 문제가 발생한다는 것을 쉽게 알 수 있다. 우리는 BigBird의 sparse attention 메커니즘을 encoder 측면에만 도입하는 데 중점을 둔다. 이는 실제 생성(generative) 애플리케이션에서 출력 시퀀스의 길이가 입력 시퀀스에 비해 일반적으로 짧기 때문이다. 예를 들어, 텍스트 요약(text summarization)의 경우, 실제 시나리오에서 (App. E.5 Tab. 18 참조) 중간 출력 시퀀스 길이는 약 200인 반면, 입력 시퀀스의 중간 길이는 3000을 초과한다. 이러한 애플리케이션에서는 encoder에 sparse attention 메커니즘을 사용하고 decoder에는 full self-attention을 사용하는 것이 더 효율적이다.

Table 4: Summarization ROUGE score for long documents.

요약 (Summarization)
문서 요약은 텍스트 문서의 짧고 정확한 요약을 생성하는 task이다. 우리는 모델 테스트를 위해 세 가지 긴 문서 데이터셋을 사용했으며, 자세한 내용은 Tab. 18에 언급되어 있다. 본 논문에서는 긴 문서의 abstractive summarization에 중점을 두는데, 이 경우 더 긴 contextual encoder를 사용하면 성능이 향상될 것으로 예상된다. 그 이유는 두 가지이다: 첫째, 핵심 내용(salient content)이 긴 문서 전체에 고르게 분포되어 있을 수 있으며, 이는 BigPatents 데이터셋 [78]의 설계 의도이기도 하다. 둘째, 긴 문서는 더 풍부한 담화 구조(discourse structure)를 보여주며, 요약이 상당히 더 abstractive하기 때문에, 더 많은 context를 관찰하는 것이 도움이 된다.
최근 [76, 107]에서 지적되었듯이, 사전학습(pretraining)은 생성 task에 도움이 되므로, 우리는 base-sized 모델에 대한 일반 목적의 MLM 사전학습으로 warm start를 수행하고, large-sized 모델에는 Pegasus [107]의 state-of-the-art 요약 전용 사전학습을 활용한다.
이러한 긴 문서 데이터셋에 대해 BigBird sparse encoder와 full decoder를 함께 학습시킨 결과는 Tab. 4에 제시되어 있다. 더 긴 context를 모델링하는 것이 상당한 성능 향상을 가져옴을 명확히 알 수 있다. 하이퍼파라미터와 함께, App. E.5에서는 더 짧지만 널리 사용되는 데이터셋에 대한 결과도 제시되어 있으며, 이는 sparse attention을 사용하는 것이 성능을 저해하지 않음을 보여준다.

5 Experiments: Genomics

최근 유전체학 데이터에 딥러닝을 활용하는 연구가 급증하고 있으며 [86, 106, 13], 이는 프로모터 부위 예측 [71], 메틸화 분석 [55], 비코딩 변이의 기능적 효과 예측 [109] 등 여러 생물학적으로 중요한 task에서 성능 향상을 가져왔다. 이러한 접근 방식들은 DNA 서열 조각을 입력으로 사용하며, DNA 내의 많은 기능적 효과가 **비국소적(non-local)**이라는 점 [12]을 고려할 때, BIGBIRD의 더 긴 입력 시퀀스 처리 능력이 유용할 것이라고 생각한다.
더 나아가, NLP에서 영감을 받아, 우리는 MLM pretraining을 통해 **풍부한 unlabeled 데이터(예: 인간 참조 유전체, Saccharomyces Genome Database)**를 활용하여 DNA 조각에 대한 강력한 contextual representation을 학습한다. 다음으로, 우리는 긴 입력 BigBIRD와 제안된 pretraining 방식이 두 가지 다운스트림 task에서 성능을 크게 향상시킨다는 것을 보여준다. 두 task에 대한 자세한 실험 설정은 App. F에 제공되어 있다.

Pre-training 및 MLM
Liang [58]에서 탐구된 바와 같이, 우리는 염기쌍(base pair) 단위로 작동하는 대신, DNA를 먼저 토큰으로 분할하여 context 길이를 더욱 늘리는 방식을 제안한다 (App. F. Fig. 7). 특히, 우리는 32K 크기의 DNA 서열에 대한 byte-pair encoding [50] 테이블을 구축했으며, 각 토큰은 평균 8.78개의 염기쌍을 나타낸다. 우리는 인간 참조 유전체(GRCh37) ${ }^{3}$에 대해 MLM objective를 사용하여 이러한 토큰의 contextual representation을 학습한다. 그런 다음, **held-out 세트에 대한 문자당 비트(BPC)**를 Tab. 5에 보고한다. 우리는 DNA의 attention 기반 contextual representation이 BPC를 향상시키며, 더 긴 context를 사용함으로써 더욱 개선된다는 것을 발견했다.

Table 5: MLM BPC

프로모터 영역 예측 (Promoter Region Prediction)
프로모터는 일반적으로 유전자 상류에 위치하며, 전사 개시(transcription initiation)가 일어나는 DNA 영역이다. 유전자 조절을 이해하는 중요한 첫 단계이기 때문에, 주어진 DNA 서열에서 프로모터 영역을 식별하는 여러 방법들이 제안되어 왔다 [99, 59, 11, 98, 71]. 해당 머신러닝 task는 주어진 DNA 조각을 프로모터 또는 비프로모터 서열로 분류하는 것이다. 우리는 Oubounyt et al. [71]이 Eukaryotic Promoter Database (EPDnew) [24] ${ }^{4}$로부터 구축한 데이터셋을 사용하였다. 우리는 위에서 사전학습된 BigBird 모델을 훈련 데이터로 fine-tuning하고, 테스트 데이터셋에 대한 F1 점수를 보고한다. Tab. 6에서 우리의 결과를 이전에 보고된 최고 방법과 비교한다. 우리는 BigBird가 이전 최고 정확도보다 5% 향상된 거의 완벽한 정확도를 달성하는 것을 볼 수 있다.

Table 6: Comparison.

크로마틴 프로파일 예측 (Chromatin-Profile Prediction)
DNA의 비코딩 영역은 단백질을 코딩하지 않는다. 대부분의 질병 및 기타 특성과 관련된 단일 염기 다형성(single-nucleotide polymorphism)은 비코딩 유전체 변이와 상관관계가 있다 [109, 46]. 따라서 DNA 비코딩 영역의 기능적 효과를 이해하는 것은 매우 중요한 task이다. Zhou와 Troyanskaya [109]에 의해 정의된 이 과정의 중요한 단계는 비코딩 유전체 서열로부터 대규모 크로마틴 프로파일링을 예측하는 것이다. 이를 위해 DeepSea [109]는 Encyclopedia of DNA Elements (ENCODE) ${ }^{5}$ 및 Roadmap Epigenomics 프로젝트 ${ }^{6}$로부터 240만 개의 비코딩 변이에 대한 919개의 크로마틴 프로파일을 수집하였다. 해당 ML task는 주어진 DNA의 비코딩 영역에 대해 919개의 크로마틴 프로파일을 예측하는 것이다. 여기에는 160개의 다른 전사 인자(TF)에 대한 690개의 전사 인자(TF) 결합 프로파일, 125개의 DNase I 민감도(DHS) 프로파일, 104개의 히스톤 마크(HM) 프로파일이 포함된다. 우리는 DNA 조각 서열로부터 이러한 기능적 효과를 예측하기 위해 919개의 이진 분류기를 공동으로 학습한다. Held-out 염색체에 대해 AUC를 Tab. 7의 baseline과 비교한 결과, 우리는 다른 task보다 더 긴 범위의 상관관계 [27]를 갖는 것으로 알려진 더 어려운 task인 HM에서 성능을 크게 향상시켰음을 확인했다.

Table 7: Chromatin-Profile Prediction

6 Conclusion

우리는 BIGBIRD를 제안한다: 이는 토큰 수에 대해 선형적인(linear) sparse attention 메커니즘이다. BIGBIRD는 여러 이론적 결과들을 만족시킨다: sequence-to-sequence 함수의 universal approximator이며, Turing complete이기도 하다. 이론적으로, 우리는 추가적인 global token의 힘을 활용하여 모델의 표현력을 보존한다. 우리는 sparse attention 메커니즘으로 전환할 때 발생하는 비용을 보여줌으로써 이러한 결과들을 보완한다. 경험적으로, BIGBIRD는 **질의응답(question answering) 및 긴 문서 분류(long document classification)**와 같은 여러 NLP task에서 state-of-the-art 성능을 제공한다. 우리는 또한 DNA를 위한 attention 기반 contextual language model을 도입하고, 이를 promoter region 예측 및 non-coding variant의 효과 예측과 같은 다운스트림 task에 대해 fine-tuning한다.

Big Bird: Transformers for Longer Sequences - Appendix

A Universal Approximators

A. 1 Notation

우리는 Pérez et al. [72]의 표기법을 따라 Transformer의 완전한 아키텍처를 형식적으로 설명하는 것으로 시작한다. Transformer encoder의 단일 layer는 $\mathbb{R}^d$ 공간의 벡터 시퀀스 $\boldsymbol{X}=\left(\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{n}\right)$를 입력으로 받아 동일한 길이의 시퀀스 $\boldsymbol{Z}=\left(\boldsymbol{z}_{1}, \ldots, \boldsymbol{z}_{n}\right)$를 반환하는 매개변수 함수 Enc이다. 각 $\boldsymbol{z}_i$ 또한 $d$ 차원 벡터이다. 우리는 시퀀스 $\boldsymbol{X}$를 $\mathbb{R}^{n \times d}$ 행렬로 상호 교환하여 사용한다. Enc는 두 가지 구성 요소를 가진다:

1. 시퀀스 $\boldsymbol{X}$를 입력으로 받아 동일한 길이와 차원의 시퀀스 $(\boldsymbol{a}_{1}, \ldots, \boldsymbol{a}_{n})$를 반환하는 attention mechanism ATTN.
2. $\mathbb{R}^d$ 공간의 벡터를 입력으로 받아 $\mathbb{R}^d$ 공간의 벡터를 반환하는 두 개의 layer로 구성된 fully connected network $O$.

그러면 $\operatorname{Enc}(\boldsymbol{X})$의 $i$-번째 출력 벡터는 다음과 같이 계산된다:

$$\boldsymbol{z}_{i}=O\left(\boldsymbol{a}_{i}\right)+\boldsymbol{a}_{i} \quad \text { where } \quad \boldsymbol{a}_{i}=\operatorname{ATTN}(\boldsymbol{X})_{i}+\boldsymbol{x}_{i}$$

이제 ATTN과 $O$를 정의하는 것이 남았으며, 이는 다음에서 설명한다. Section 2에서 설명했듯이, attention mechanism은 세 가지 함수 $Q, K, V: \mathbb{R}^d \rightarrow \mathbb{R}^m$에 의해 매개변수화된다. 본 논문에서는 이들이 단순히 행렬 곱셈이라고 가정한다: $Q(\boldsymbol{x})=\boldsymbol{x} W_{Q}$, $K(\boldsymbol{x})=\boldsymbol{x} W_{K}$, 그리고 $V(\boldsymbol{x})=\boldsymbol{x} W_{V}$이다. 여기서 $W_{Q}, W_{K}, W_{V} \in \mathbb{R}^{d \times m}$이고 $W_{V} \in \mathbb{R}^{d \times d}$이다. 실제로는 multi-headed attention이 사용된다. 즉, 우리는 하나의 Query/Key/Value 가중치 행렬 세트가 아니라, $h=1, \ldots, H$에 대해 $H$개의 세트인 $W_{Q}^{h}, W_{V}^{h}, W_{K}^{h}$를 가진다. 따라서 $[n]$에 대한 **방향 그래프 $D$**의 경우, 일반화된 attention mechanism의 $i$-번째 출력 벡터는 다음과 같다:

$$\operatorname{ATTN}_{D}(\boldsymbol{X})_{i}=\sum_{h=1}^{H} \sigma\left(\left(\boldsymbol{x}_{i} W_{Q}^{h}\right)\left(\boldsymbol{X}_{N(i)} W_{K}^{h}\right)^{T}\right) \cdot\left(\boldsymbol{X}_{N(i)} W_{V}^{h}\right)$$

여기서 $N(i)$는 $D$에서 노드 $i$의 out-neighbors 집합을 나타낸다. 다시 말해, $D$의 아크(방향성 엣지) 집합은 우리 attention mechanism이 고려할 내적(inner product) 집합을 나타낸다. 또한 $\sigma$는 softmax 또는 hardmax와 같은 scoring function임을 상기하라. 마지막으로, 출력 fully connected network는 다음과 같이 정의한다:

$$O\left(\boldsymbol{a}_{i}\right)=\operatorname{ReLU}\left(\boldsymbol{a}_{i} W_{1}+b_{1}\right) W_{2} \cdot+b_{2}$$

여기서 $W_{1} \in \mathbb{R}^{d \times q}, W_{2} \in \mathbb{R}^{q \times d}, b_{1} \in \mathbb{R}^{p}$, 그리고 $b_{2} \in \mathbb{R}^{d}$는 출력 네트워크 $O$의 매개변수이다. 추가 표기법 (Additional Notation)
몇 가지 유용한 추가 표기법을 소개한다. $[a, b)_{\delta}=\left\{a, a+\delta, \ldots, a+\left\lfloor\frac{b-a}{\delta}\right\rfloor \cdot \delta\right\}$라고 하자. 따라서 $[0,1)_{\delta}=\{0, \delta, 2 \delta, \ldots,(1-\delta)\}$이다. 우리는 $\mathbf{1}[\mathcal{E}]$를 **지시 변수(indicator variable)**로 사용한다. 이벤트 $\mathcal{E}$가 발생하면 1이고, 그렇지 않으면 0이다.

A. 2 Proof

이 섹션에서는 정리 1(theorem 1)의 전체 증명을 제시한다. 증명은 세 부분으로 구성된다. 첫 번째와 세 번째 부분은 주로 표준적인 기법을 따를 것이다. 주요 혁신은 두 번째 부분에 있다.

A.2.1 Approximate $\mathcal{F}_{C D}$ by piece-wise constant functions

먼저, 우리는 $(0,1)$ 구간을 granularity $\delta$를 가진 그리드 $G_{\delta}$로 적절하게 분할하는 것을 고려한다. 이를 위해 Yun et al. [104]의 Lemma 8을 사용하며, 완전성을 위해 이를 다시 기술한다:

Lemma 1 (Lemma 8 [104]). 임의의 $\underline{f} \in \mathcal{F}_{C D}$와 $1 \leq p \leq \infty$에 대해, $d_{p}(f, \bar{f}) \leq \frac{\epsilon}{3}$를 만족하는 piece-wise constant function $\bar{f}$가 존재하도록 하는 $\delta>0$가 존재한다. 구체적으로, $\bar{f}$는 다음과 같이 정의된다:

$$\bar{f}(X)=\sum_{P \in \mathbb{G}_{\delta}} f(P) \cdot \mathbf{1}\left[\|\operatorname{ReLU}(X-P)\|_{\infty} \leq \delta\right]$$

Transformer는 positional embedding $E$를 학습할 수 있으므로, 일반성을 잃지 않고 **변환된 함수(translated function)**를 고려할 수 있다. 특히, 다음과 같이 정의한다:

$$E=\left[\begin{array}{ccccc} 0 & 0 & 0 & \ldots & 0 \\ \delta^{-d} & \delta^{-d} & \delta^{-d} & \ldots & \delta^{-d} \\ \delta^{-2 d} & \delta^{-2 d} & \delta^{-2 d} & \ldots & \delta^{-2 d} \\ \vdots & & & & \\ \delta^{-(n-1) d} & \delta^{-(n-1) d} & \delta^{-(n-1) d} & \ldots & \delta^{-(n-1) d} \end{array}\right]$$

우리는 $g(X)=f(X-E)$를 근사하려고 한다. 여기서 $g$는 도메인 $[0,1]^{d} \times\left[\delta^{-d}, \delta^{-d}+1\right]^{d} \times \cdots \times\left[\delta^{-(n-1) d}, \delta^{-(n-1) d}+1\right]^{d}$에서 정의된다. 이를 위해, Lemma 1을 적절히 수정하여 **이산화된 그리드(discretized grid)**를 고려할 것이다:

$$\mathbf{G}_{\delta}^{E}:=[0,1]_{\delta}^{d} \times\left[\delta^{-d}, \delta^{-d}+1\right]_{\delta}^{d} \times \cdots \times\left[\delta^{-(n-1) d}, \delta^{-(n-1) d}+1\right]_{\delta}^{d}$$

따라서, 다음과 같이 정의된 함수 $\bar{f}: \mathbf{G}_{\delta}^{E} \rightarrow \mathbb{R}^{n \times d}$를 근사하는 것으로 충분하다:

$$\bar{f}(X)=\sum_{P \in \mathbf{G}_{\delta}^{E}} f(P-E) \cdot \mathbf{1}\left[\|\operatorname{ReLU}(X-P)\|_{\infty} \leq \delta\right]$$

A.2.2 Contextual Mappings and Sparse Attention Mechanisms

이 섹션 전체에서 우리는 인덱스 0에 추가적인 global token을 가지고 있으며, 모든 벡터에 추가 차원이 하나 더 붙어 있는 함수를 가정한다. 후자의 가정은 Feed-Forward Network를 사용하여 sparse 차원을 추가할 수 있으므로 일반성을 잃지 않는다. 특히, 우리는 $X \in \mathbb{R}^{(n+1) \times(d+1)}$를 $X=\left(x_{0}, x_{1}, \ldots, x_{n}\right)$으로 표기한다. 우리의 함수는 $\mathbf{G}_{\delta}^{E} \subset \mathbb{R}^{n \times d}$에 대해서만 정의되지만, 첫 번째 열을 무시하도록 자연스럽게 함수를 수정할 수 있다. 과도한 복잡성을 피하기 위해, 함수 값은 마지막 $n$개 열에 대해 평가된다고 가정한다.

이 섹션의 주요 아이디어는 contextual mapping을 사용하여 Transformer가 모든 이산화된(discretized) 함수를 계산할 수 있도록 하는 것이다. Contextual mapping은 각 튜플 $(X, x_{i})$에 대한 고유한 인코딩이며, 여기서 $X \in \mathbf{G}_{\delta}^{E}$이고, 모든 $i \in[n]$에 대해 각 열 $x_{i} \in\left[\delta^{-(i-1) d}, \delta^{-(i-1) d}+1\right)_{\delta}^{d}$이다. 아래에 우리의 설정에 맞게 조정된 정의를 다시 제시한다. 정의 2 (정의 3.1 [104]). (Contextual Mapping) Contextual mapping은 다음을 만족하는 함수 $q: \mathbf{G}_{\delta}^{E} \rightarrow \mathbb{R}^{n}$이다:

1. 어떤 $P \in \mathbf{G}_{\delta}^{E}$에 대해서도, $q(P)$는 **서로 다른 항목(distinct entries)**을 포함한다.
2. 서로 다른 두 $P, P^{\prime} \in \mathbf{G}_{\delta}^{E}$에 대해, $q(P)$와 $q\left(P^{\prime}\right)$의 모든 항목은 서로 다르다.

증명의 핵심 기술적 참신성은 sparse attention mechanism만을 사용하여 contextual mapping을 계산하는 것이다. 우리는 특정 범위에 있는 벡터의 항목만 이동시키는 "selective shift" 연산자를 생성한다. 이 shift 연산자를 전략적으로 사용하여 프로세스 끝에서 contextual mapping을 얻도록 할 것이다. 아래 보조정리는 [104]의 보조정리 6 증명의 일부를 기반으로 하며, sparse attention mechanism을 사용하여 적절한 "selective" shift 연산자를 구현할 수 있음을 명시한다. 보조정리 2. 함수 $\psi: \mathbb{R}^{(n+1) \times(d+1)} \times \mathbb{R}^{2} \rightarrow \mathbb{R}^{(n+1) \times 1}$와 벡터 $u \in \mathbb{R}^{d+1}$, 그리고 directed graph $D$에 기반한 sparse attention mechanism이 주어졌을 때, 우리는 입력으로 행렬 $X \in \mathbb{R}^{(n+1) \times(d+1)}$를 받고 $X+\rho \cdot \psi_{u}\left(X, b_{1}, b_{2}\right)$를 출력하는 selective shift 연산자를 구현할 수 있다. 여기서

$$\psi_{u}\left(Z ; b_{1}, b_{2}\right)_{i}= \begin{cases}\left(\max _{j \in N(i)} u^{T} Z_{j}-\min _{j \in N(i)} u^{T} Z_{j}\right) e_{1} & \text { if } b_{1} \leq u^{T} Z_{j} \leq b_{2} \\ 0 & \text { else. }\end{cases}$$

여기서 $e_{1} \in R^{d+1}$는 $(1,0, \ldots, 0)$을 나타낸다. 증명. sparse attention mechanism으로 구현될 수 있는 다음 함수를 고려하자:

$$\tilde{\psi}(X, b)_{i}=\sigma_{H}\left[\left(u^{T} \cdot X_{i}\right)^{T} \cdot\left(u^{T} X_{N(i)}-b 1_{N(i)}^{T}\right) e^{(1)}\left(u^{T} X_{N(i)}\right)\right]$$

이는 Key, Query, Value 함수가 단순히 $X$의 affine 변환이기 때문이다. 어떤 그래프 $D$가 주어지더라도, 위 함수는 다음으로 평가될 것이다:

$$\tilde{\psi}(Z ; b)_{i}= \begin{cases}\left(\max _{j \in N(i)} u^{T} Z_{j}\right) e_{1} & \text { if } u^{T} Z_{j}>b \\ \left(\min _{j \in N(i)} u^{T} Z_{j}\right) e_{1} & \text { if } u^{T} Z_{j}<b\end{cases}$$

따라서 우리는 $\tilde{\psi}\left(Z ; b_{Q}\right)-\tilde{\psi}\left(Z ; b_{Q^{\prime}}\right)$가 다음을 만족한다고 말할 수 있다:

$$\psi\left(Z ; b_{1}, b_{2}\right)_{i}= \begin{cases}\left(\max _{j \in N(i)} u^{T} Z_{j}-\min _{j \in N(i)} u^{T} Z_{j}\right) e_{1} & \text { if } b_{1} \leq u^{T} Z_{j} \leq b_{2} \\ 0 & \text { else }\end{cases}$$

다음 보조정리는 증명의 핵심이며, 위 selective shift 연산자를 사용하여 contextual mapping을 구성한다. 보조정리 3. 함수 $g_{c}: \mathbb{R}^{(n+1) \times(d+1)} \rightarrow \mathbb{R}^{(n+1)}$와 고유한 벡터 $u$가 존재하여, 모든 $P \in \mathbf{G}_{\delta}^{E}$에 대해 $g_{c}(P):=\langle u, g(P)\rangle$가 $P$의 contextual mapping 속성을 만족한다. 또한, $D$가 star graph를 포함하는 한, $g_{c} \in \mathcal{T}_{D}^{2,1,1}$는 sparse attention layer의 합성(composition)을 사용하여 구현될 수 있다.

증명. $u \in \mathbb{R}^{d+1}=\left[1, \delta^{-1}, \delta^{-2}, \ldots, \delta^{-d+1}, \delta^{-n d}\right]$로 정의하고 $X_{0}=(0, \ldots, 0,1)$로 두자. 우리는 모든 열 $x_{1}, \ldots, x_{n}$이 0으로 추가된다고 가정하여 $\left\langle x_{i}, x_{0}\right\rangle=0$이라고 가정할 것이다. 각 token에 전체 context를 성공적으로 인코딩하기 위해, 우리는 shift 연산자를 원래의 열 $1, \ldots, n$과 global 열 0을 대상으로 교차(interleave)하여 적용할 것이다. 열 $i$가 대상이 된 후, $u$와의 내적은 처음 $i$개 열의 전체 context를 인코딩할 것이다. 다음으로, 이 context를 고려하기 위해 global token을 shift할 것이다. 이는 이후 나머지 열에 의해 사용될 수 있다. $i \in\{0,1, \ldots, n\}$에 대해, 우리는 처음에 내적 $\left\langle u, x_{i}\right\rangle$를 $l_{i}$로 나타낼 것이다. $i \in\{1, \ldots, n\}$에 대해 $i$번째 열이 변경된 후의 $\left\langle u, x_{i}\right\rangle$를 $f_{i}$로 사용하고, $k$번째 단계 후의 $\left\langle u, x_{0}\right\rangle$를 $f_{0}^{k}$로 사용할 것이다. global token은 각 단계에서 내적이 변경되므로 추가로 구별해야 한다. 처음에 $X \in \mathbf{G}_{\delta}^{E}$가 주어졌을 때, 다음이 참이다:

$$\begin{aligned} \delta^{-(i-1) d} & \leq\left\langle u, X_{i}\right\rangle \leq \delta^{-i d}-\delta \quad \text { for all } i \in[n] \\ \delta^{-(n+1) d} & =\left\langle u, X_{0}\right\rangle \end{aligned}$$

모든 $l_{i}$는 $l_{1}<l_{2}<\cdots<l_{n}<l_{0}$와 같이 서로 다른 버킷에 정렬된다는 점에 유의하라. 우리는 이를 $i \in\{1, \ldots, n\}$으로 인덱싱된 단계(phase)로 수행한다. 각 단계는 두 가지 다른 부분으로 구성된다: Low shift 연산: 이 연산은 다음 형태를 가질 것이다:

$$X \leftarrow X+\delta^{-d} \psi(X, v-\delta / 2, v+\delta / 2)$$

여기서 v \in\left[\delta^{-i d}\right), \delta^{-(i+1) d}\right)_{\delta}이다. 이 범위는 $l_{i}$만 범위 내에 있고 다른 $l_{j} j \neq i$는 범위 내에 있지 않도록 선택된다. 이는 정확히 $i$번째 열 $x_{i}$를 shift하여 새로운 내적 $f_{i}=\left\langle u, x_{i}\right\rangle$가 $l_{i}$보다 상당히 커지도록 할 것이다. 또한, $X$의 다른 열은 영향을 받지 않을 것이다. High shift 연산: 이 연산은 다음 형태를 가질 것이다:

$$X \leftarrow X+\delta^{-n d} \cdot \psi(X, v-\delta / 2, v+\delta / 2)$$

여기서 $v \in\left[S_{i}, T_{i}\right)_{\delta}$이다. 범위 $\left[S_{i}, T_{i}\right)_{\delta}$는 열 $x_{0}$ (global token에 해당)만 영향을 미치고 다른 열은 영향을 미치지 않도록 선택된다. 특히, 이는 global token을 추가로 $\delta^{-n d}$만큼 shift할 것이다. $\tilde{f}_{0}^{i}$를 $i$번째 high 연산이 끝날 때의 $\tilde{f}_{0}^{i}=\left\langle u, x_{0}\right\rangle$ 값으로 나타내자. 각 단계는 열 $i$에 대한 shift 연산과 global token 업데이트를 교차(interleave)한다. 각 단계 후, 업데이트된 $i$번째 열 $f_{i}=\left\langle u, x_{i}\right\rangle$는 모든 $l_{1}, \ldots, l_{i}$의 값을 인코딩하는 고유한 token을 포함할 것이다. high 업데이트 후, $\tilde{f}_{0}^{i}=\left\langle u, x_{0}\right\rangle$는 처음 $i$개 token에 대한 정보를 포함할 것이다. 마지막으로, 모든 $k \in\{0,1, \ldots, n\}$에 대해 다음 상수를 정의한다.

$$\begin{aligned} T_{k}=( & \left.\delta^{-(n+1) d}+1\right)^{k} \cdot \delta^{-n d}-\sum_{t=2}^{k}\left(\delta^{-(n+1) d}+1\right)^{k-t}\left(2 \delta^{-n d-d}+\delta^{-n d}+1\right) \delta^{-t d} \\ & -\left(\delta^{-(n+1) d}+1\right)^{k-1}\left(\delta^{-n d-d}+\delta^{-n d}\right) \delta^{-d}-\delta^{-(k+1) d} \end{aligned}$$ $$\begin{aligned} S_{k}=( & \left.\delta^{-(n+1) d}+1\right)^{k} \cdot \delta^{-n d}-\sum_{t=2}^{k}\left(\delta^{-(n+1) d}+1\right)^{k-t}\left(2 \delta^{-n d-d}+\delta^{-n d}+1\right) \delta^{-(t-1) d} \\ & -\left(\delta^{-(n+1) d}+1\right)^{k-1}\left(\delta^{-n d-d}+\delta^{-n d}\right)-\delta^{-k d} \end{aligned}$$

각 $k$단계 후, 우리는 다음 불변량(invariants)을 유지할 것이다:

1. 모든 $k \in\{0,1, \ldots, n\}$에 대해 $S_{k}<\tilde{f}_{0}^{k}<T_{k}$이다.
2. $T_{k-1} \leq f_{k}<S_{k}$이다.
3. $k$번째 단계 후 내적의 순서는 다음과 같다:

$$l_{k+1}<l_{k+2} \cdots<l_{n}<f_{1}<f_{2}<\cdots<f_{k}<\tilde{f}_{0}^{k}$$

기저 사례(Base case) $k=0$인 경우는 $S_{0}=\delta^{-(n+1) d}, T_{0}=\delta^{-(n+1) \cdot d}+\delta$로 설정하므로 자명하다. 첫 번째 비자명한 경우는 $k=1$이다.

귀납 단계(Inductive Step) 먼저, low shift 연산은 $\left[\delta^{-(k-1) d}, \delta^{-k d}\right)_{\delta}$ 범위에서 수행된다. 불변량에 따라, 우리는 이 shift에 의해 영향을 받는 열 $x_{k}$가 하나만 존재한다는 것을 안다. 특히, 열 $k$에 대해 $\max _{j \in N(k)}\left\langle u, x_{j}\right\rangle=\left\langle u, x_{0}\right\rangle=\tilde{f}_{0}^{k-1}$일 것이다. 최솟값은 $l_{k}$이다. 따라서 업데이트는 $f_{k}=\delta^{-d}\left(\tilde{f}_{0}^{k-1}-l_{k}\right)+l_{k}$가 될 것이다. $\delta$가 충분히 작으면 $f_{k} \geq \tilde{f}_{0}^{k-1}$임을 관찰하라. 따라서 이 연산 후의 전체 순서는 다음과 같다:

$$l_{k}+1<l_{k+2} \cdots<l_{n}<f_{1}<f_{2}<\cdots<\tilde{f}_{0}^{k-1}<f_{k}$$

이제 $\left[S_{k-1}, T_{k-1}\right)_{\delta}$ 범위에서 higher selective shift 연산자를 수행할 때, global token의 내적 $\tilde{f}_{0}^{k-1}$만 이 범위에 있으므로, shift 연산자에 의해 영향을 받는 유일한 열이 될 것이다. global token은 전체 범위에 걸쳐 작동하며, 식 (2)로부터 $f_{k}=\max _{i \in[n]}\left\langle u, x_{i}\right\rangle$이고 $l_{k+1}=\min _{i \in[n]}\left\langle u, x_{i}\right\rangle$임을 안다. 새로운 값 $\tilde{f}_{0}^{k}=\delta^{-n d} \cdot\left(f_{k}-l_{k+1}\right)+\tilde{f}_{0}^{k-1}$이다. 전개하고 단순화하면 다음을 얻는다:

$$\begin{aligned} \tilde{f}_{0}^{k} & =\delta^{-n d} \cdot\left(f_{k}-l_{k+1}\right)+\tilde{f}_{0}^{k-1} \\ & =\delta^{-n d} \cdot\left(\delta^{-d}\left(\tilde{f}_{0}^{k-1}-l_{k}\right)+l_{k}-l_{k+1}\right)+\tilde{f}_{0}^{k-1} \\ & =\delta^{-(n+1) d} \cdot\left(\tilde{f}_{0}^{k-1}-l_{k}\right)+\delta^{-n d}\left(l_{k}-l_{k+1}\right)+\tilde{f}_{0}^{k-1} \\ & =\left(\delta^{-(n+1) d}+1\right) \tilde{f}_{0}^{k-1}-\left(\delta^{-n d-d}+\delta^{-n d}\right) l_{k}-l_{k+1} \end{aligned}$$

위 식을 재귀적으로 전개하면 다음을 얻는다:

$$\begin{aligned} = & \left(\delta^{-(n+1) d}+1\right)^{k} \cdot \tilde{f}_{0}^{0}-\sum_{t=2}^{k}\left(\delta^{-(n+1) d}+1\right)^{k-t}\left(2 \delta^{-n d-d}+\delta^{-n d}+1\right) l_{t} \\ & -\left(\delta^{-(n+1) d}+1\right)^{k-1}\left(\delta^{-n d-d}+\delta^{-n d}\right) l_{1}-l_{k+1} \end{aligned}$$

$\tilde{f}_{0}^{0}=\delta^{-n d}$이고 각 $l_{i}<\delta^{-i d}$임을 알기 때문에, 이를 대입하여 식 UP을 얻을 수 있고, $l_{i} \geq \delta^{-(i-1) d}$를 사용하여 하한(lower-bound) 식 LP를 얻을 수 있다. 구성상, 우리는 $S_{k} \leq \tilde{f}_{0}^{k}<T_{k}$임을 안다. 충분히 작은 $\delta$에 대해, $S_{k} \leq \tilde{f}_{0}^{k}<T_{k}$ 모두 본질적으로 지배적인 항 $\approx O\left(\delta^{-n(k+1) d-k d}\right)$이며 모든 하위 차수 항은 중요하지 않음을 관찰하라. 결과적으로 $f_{k}>\delta^{-d}\left(\tilde{f}_{0}^{k-1}-l_{k}\right)>T_{k-1}$임을 즉시 알 수 있으며, 따라서 불변량 2도 만족됨을 알 수 있다. 열 $k$와 global token만 영향을 받으므로, 불변량 3도 만족됨을 알 수 있다. $n$번의 반복 후, $\tilde{f}_{0}^{n}$는 모든 $P \in \mathbf{G}_{\delta}^{E}$에 대한 고유한 인코딩을 포함한다. 모든 token이 서로 다르도록 하기 위해, 우리는 모든 $v \in\left[S_{1}, T_{n}\right)_{\delta}$에 대해 추가 layer $X=X+\delta^{-n^{2} d} \psi(X, v-\delta / 2, v+\delta / 2)$를 추가할 것이다. 이는 모든 $P, P^{\prime} \in \mathbf{G}_{\delta}^{E}$에 대해 $q(P)$와 $q\left(P^{\prime}\right)$의 각 항목이 서로 다르도록 보장한다. $\square$

이전 보조정리는 sparse transform만을 사용하여 contextual mapping을 계산할 수 있음을 보여준다. 이제 다음 보조정리를 사용하여 contextual mapping과 feed-forward layer를 사용하여 함수 $f$의 원하는 출력에 정확하게 매핑할 수 있음을 보여준다. 보조정리 4 (보조정리 7 [104]). 보조정리 3의 함수 $g_{c}$가 주어졌을 때, 우리는 $\Phi$에서 활성화 함수를 가진 $O\left(n \delta^{-n d}\right)$개의 feed-forward layer (숨겨진 차원 $q=1$)로 구성된 함수 $g_{v}: \mathbb{R}^{(n+1) \times(d+1)} \rightarrow \mathbb{R}^{(n+1) \times d}$를 구성할 수 있으며, $g_{v}$는 모든 $j \in\{1, \ldots, n\}$에 대해 다음과 같이 정의된다:

$$g_{v}^{t k n}\left(g_{c}(L)_{j}\right)=f(L)_{j}$$

A.2.3 Approximating modified Transformers by Transformers

이전 섹션에서는 hardmax operator $\sigma_{H}$와 집합 $\Phi$에 속하는 activation function을 사용하는 Transformer를 가정했다. 다음 보조정리가 보여주듯이 이는 일반성을 잃지 않는다. 보조정리 5 (보조정리 9 [104]). 각 $g \in \overline{\mathcal{T}}^{2,1,1}$ 및 $1 \leq p \leq \infty$에 대해, $d_{p}(g, \bar{g}) \leq \epsilon / 3$를 만족하는 $g \in \mathcal{T}^{2,1,4}$가 존재한다.

위 보조정리를 보조정리 3과 결합하면, 우리의 주요 결과인 다음 정리를 얻는다: 정리 2. $1 \leq p \leq \infty$ 및 $\epsilon>0$이라고 하자. 이때 $d_{p}(f, g) \leq \epsilon$의 비율을 달성하는 Transformer 네트워크 $g \in \mathcal{T}_{D}^{2,1,4}$가 존재하며, 여기서 $D$는 sparse graph이다.

BigBird와 관련된 sparsity graph는 star network를 포함하므로, 이는 compact domain에서 모든 연속 함수를 표현할 수 있음을 알 수 있다.

Sparse Transformer의 Universal Approximability에 대한 동시대 연구
Yun et al. [105]의 동시대 연구 또한 linear connection을 가진 sparse Transformer가 compact domain에서 sequence-to-sequence 함수를 포착하는 능력을 병렬적으로 탐구했음을 언급하고자 한다.

B Turing Completeness

이 섹션에서는 Pérez et et al. [72]의 설정으로 우리의 결과를 확장할 것이다. 우리의 설명은 주로 그들의 증명 구조를 따르겠지만, 몇 가지 변경 사항을 적용할 것이다. 설명을 자체적으로 완결성 있게 만들기 위해 일부 보조정리(lemma)들을 수정하여 반복한다.

B. 1 Notation

Transformer Decoder
Turing machine를 시뮬레이션하기 위해 Transformer에는 encoder와 decoder가 모두 필요하다. 우리는 encoder에 대해 App. A.1에서 사용된 것과 동일한 표기법을 활용한다. decoder는 encoder와 유사하지만, 외부 key-value 벡터 쌍($\boldsymbol{K}^{\mathbf{e}} \in \mathbb{R}^{n \times m}, \boldsymbol{V}^{\mathbf{e}} \in \mathbb{R}^{n \times d}$) 에 대한 추가적인 attention을 포함하며, 이들은 일반적으로 encoder stack에서 제공된다.
Transformer decoder의 단일 layer는 Dec라는 parametric function으로, $\mathbb{R}^{d}$ 차원의 벡터 시퀀스 $\boldsymbol{Y}_{j}=\left(\boldsymbol{y}_{1}, \ldots, \boldsymbol{y}_{j}\right)$와 외부 ($\boldsymbol{K}^{\mathbf{e}}, \boldsymbol{V}^{\mathbf{e}}$)를 입력으로 받아, 동일한 길이의 벡터 시퀀스 $\boldsymbol{Z}_{j}=\left(\boldsymbol{z}_{1}, \ldots, \boldsymbol{z}_{j}\right)$를 반환한다. 각 $\boldsymbol{z}_{i}$ 또한 $d$ 차원 벡터이다. Dec는 Enc보다 하나 더 많은 세 가지 구성 요소를 가진다:

1. Attention mechanism ATTN: 시퀀스 $\boldsymbol{Y}_{j}$를 입력으로 받아 동일한 길이와 차원의 시퀀스 ($\boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{j}$)를 반환한다.
2. Cross-attention mechanism CrossAttn: 시퀀스 ($\boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{j}$)와 외부 ($\boldsymbol{K}^{\mathbf{e}}, \boldsymbol{V}^{\mathbf{e}}$)를 입력으로 받아 시퀀스 ($\boldsymbol{a}_{1}, \ldots, \boldsymbol{a}_{j}$)를 반환하며, 각 $\boldsymbol{a}_{i} \in \mathbb{R}^{d}$이다.
3. Two-layer fully connected network $O$: $\mathbb{R}^{d}$ 차원의 벡터를 입력으로 받아 $\mathbb{R}^{d}$ 차원의 벡터를 반환한다.

이때 $\operatorname{Dec}\left(\boldsymbol{Y}_{j} ; \boldsymbol{K}^{\mathbf{e}}, \boldsymbol{V}^{\mathbf{e}}\right)$의 $i$-번째 출력 벡터는 다음과 같이 계산된다:

$$z_{i}=O\left(a_{i}\right)+a_{i}$$

여기서

$$\boldsymbol{a}_{i}=\operatorname{CrOSSATTN}\left(\boldsymbol{p}_{i}, \boldsymbol{K}^{\mathbf{e}}, \boldsymbol{V}^{\mathbf{e}}\right)+\boldsymbol{p}_{i}$$

그리고

$$\boldsymbol{p}_{i}=\operatorname{ATTN}_{D}\left(\boldsymbol{Y}_{j}\right)_{i}+\boldsymbol{y}_{i}$$

ATTN $_{D}$와 $O$는 App. A.1에 정의된 바와 같으며, CrossAttn을 정의하는 것만 남았다. multi-head cross-attention의 $i^{\text {th }}$ 출력 벡터는 다음과 같이 주어진다:

$$\operatorname{CrossAttn}\left(\boldsymbol{Y}_{j}\right)_{i}=\sum_{h=1}^{H} \sigma\left(\left(\boldsymbol{y}_{i} W_{Q}^{h}\right)\left(\boldsymbol{K}^{(e)} W_{K}^{h}\right)^{T}\right) \cdot\left(\boldsymbol{V}^{(e)} W_{V}^{h}\right)$$

여기서 $W_{Q}^{h}, W_{K}^{h}, W_{V}^{h} \in \mathbb{R}^{d \times m}, W_{V}^{h} \in \mathbb{R}^{d \times d}$이며, 모든 $h=1, \ldots H$ head에 대해 적용된다.

Turing Machine
우리는 Pérez et al. [72]에서 사용된 Turing Machine 설정을 활용할 것이다 (섹션 B.4 참조). Turing Machine $M=\left(Q, \Sigma, \delta, q_{\text {init }}, F\right)$ 가 주어졌을 때, 다음 표기법을 사용한다:

$$\begin{aligned} q^{(j)} & : \text { 시간 } j \text { 에서 Turing machine } M \text { 의 상태. } \\ s^{(j)} & : \text { 시간 } j \text { 에서 } M \text { 의 헤드 아래에 있는 기호. } \\ v^{(j)} & : \text { 시간 } j \text { 에서 } M \text { 이 기록한 기호. } \\ m^{(j)} & : \text { 시간 } j \text { 에서 } M \text { 의 전이(transition)에서의 헤드 방향. } \end{aligned}$$

벡터 표현 (Vector representations)
기호 $s \in \Sigma$에 대해, $\llbracket s \rrbracket$는 $\mathbb{Q}^{|\Sigma|}$에서의 one-hot 벡터 표현을 나타낸다. 우리의 시뮬레이션에서 사용되는 모든 Transformer 중간 벡터는 차원 $d=2|Q|+4|\Sigma|+16$을 가진다. Pérez et al. [72]에 비해 5개의 추가 차원을 사용한다는 점에 유의하라. 우리는 Pérez et al. [72]에서 사용된 관례를 따르며, $\mathbb{Q}^{d}$ 차원의 벡터 $\boldsymbol{v}$를 다음과 같이 네 그룹의 값으로 배열하여 표현한다:

$$\begin{aligned} \boldsymbol{v}=[ & \boldsymbol{q}_{1}, \boldsymbol{s}_{1}, x_{1}, \\ & \boldsymbol{q}_{2}, \boldsymbol{s}_{2}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}, \\ & \boldsymbol{s}_{3}, x_{7}, \boldsymbol{s}_{4}, \\ & \left.x_{8}, x_{9}, x_{10}, x_{11}, x_{12}, x_{13}, x_{14}, x_{15}, x_{16} \quad\right] \end{aligned}$$

여기서 $\boldsymbol{q}_{i} \in \mathbb{Q}^{|Q|}, \boldsymbol{s}_{i} \in \mathbb{Q}^{|\Sigma|}$, 그리고 $x_{i} \in \mathbb{Q}$이다.

B. 2 Details of the Simulation

이 섹션에서는 시뮬레이션 전략을 구현하는 데 필요한 encoder와 decoder의 아키텍처에 대해 더 자세히 설명한다.

높은 수준의 개요 (High Level Overview): 주어진 Turing machine $M$에 대해, 우리는 적절한 encoder와 decoder를 갖춘 Transformer $\mathcal{T}_{D}$가 $M$의 각 실행 단계를 시뮬레이션할 수 있음을 보일 것이다. 우리의 시뮬레이션 전략은 대부분 Pérez et al. [72]를 따르지만, sparse attention 메커니즘을 사용할 것이다.
주요 아이디어는 현재 Turing machine의 상태 $q^{(j)}$와 헤드 아래의 기호 $s^{(j)}$를 모든 시간 단계 $j$에 대해 decoder 시퀀스 $\boldsymbol{Y}$의 일부로 유지하여, 해당 Turing machine의 전이 $\delta\left(q^{(j)}, s^{(j)}\right)=\left(q^{(j)}, v^{(j)}, m^{(j)}\right)$를 항상 시뮬레이션할 수 있도록 하는 것이다.
핵심적인 차이점은 Pérez et al. [72]의 Lemma B.4에서 발생하는데, 여기서는 하나의 단계에서 tape history로부터 적절한 기호를 선택하기 위해 full attention이 사용된다. sparse attention으로 동일한 작업을 수행하기 위해, 우리는 max의 associative property를 활용하여 여러 단계에 걸쳐 기호 선택을 분해할 것이다.
따라서 Pérez et al. [72]와 달리, 우리의 sparse Transformer $\mathcal{T}_{D}$의 한 decoding 단계는 Turing machine $M$의 한 단계에 해당하지 않는다. 특히, 우리는 두 가지 유형의 단계를 가질 것이다:

• compute step: $M$의 상태 업데이트에 해당
• intermediate step: max를 집계하는 데 해당 (이는 다시 기호 선택에 사용됨)

$\mathcal{T}_{D}$의 단계를 $i$라고 하고, decoder의 단계 $i$에서 시뮬레이션되는 $M$의 단계를 $g(i)$라고 하자. 각 decoding 단계에서 우리는 현재 Turing machine의 상태 $q^{g(i)}$와 헤드 아래의 기호 $s^{g(i)}$를 $\boldsymbol{y}_{i}$에 유지하고자 한다.
대략 $O(\sqrt{i})$개의 intermediate step 동안 상태는 동일하게 유지되며, 우리는 sparse attention을 통해 관련 과거 출력 기호에 대한 정보를 집계할 것이다. intermediate step 동안 동일한 상태를 유지하기 위해, 우리는 추가적인 switching layer를 도입한다 (App.B.2.3).
마지막으로, 다음 compute step에서 우리는 새로운 상태 $q^{g(i)+1}$, 새로운 헤드 이동 $m^{g(i)}$, 그리고 기록될 새로운 출력 기호 $v^{g(i)}$로 전이할 것이다.
이로써 우리는 주어진 Turing machine $M$을 완전히 시뮬레이션할 수 있다. 결과적으로, 우리는 다음 주요 정리를 증명할 수 있다:

Theorem 3. $O(n)$개의 내적(inner products)을 사용하는 sparse attention 메커니즘이 존재하며, 이 sparse attention 메커니즘을 사용하는 결과적인 Transformer Network 클래스는 Turing Complete하다.

Encoder

[72]에서와 같이, 우리는 단일 layer encoder를 사용하며, 여기서 결과 $\boldsymbol{K}^{(e)}$는 **위치 임베딩(position embedding)**을 포함하고, $\boldsymbol{V}^{(e)}$는 one-hot symbol representation을 포함한다.

Decoder

Decoder를 위한 Sparse Self-Attention 메커니즘
이 섹션에서는 decoder의 sparse graph $D$의 특정 인스턴스를 고려한다. 우리는 그 edge들이 다음 관계에 의해 주어진다고 정의한다: $\forall j \in \mathbb{N}_{+}, 1 \leq k \leq j+1$,

$$\begin{aligned} & \left(\frac{j(j+1)}{2}+k, \frac{k(k+1)}{2}\right) \text { and } \\ & \left(\frac{j(j+1)}{2}+k, \frac{j(j+1)}{2}+k\right) \text { if } k>1 \text { else }\left(\frac{j(j+1)}{2}+1, \frac{j(j+1)}{2}\right) . \end{aligned}$$

이 그래프는 BIGBIRD의 특수한 경우로 볼 수 있다. 여기서 첫 번째 유형의 edge는 random edge의 구현이며, 두 번째 유형의 edge는 locality에 해당한다. 또한, 이 그래프는 decoder의 left-to-right 제약 조건을 만족한다. 즉, 어떤 노드도 미래의 노드를 attend하지 않는다.

Figure 2: Transformer step과 원래 Turing machine step 간의 매핑.

Embedding 및 Positional Encoding
우리의 구성은 decoder를 위한 **다른 positional encoding $\operatorname{pos}_{\text {Dec }}: \mathbb{N} \rightarrow \mathbb{Q}^{d}$**를 필요로 한다:

$$\begin{aligned} \operatorname{pos}_{\operatorname{Dec}}(i)=[ & 0, \ldots, 0 \\ & 0, \ldots, 0 \\ & 0, \ldots, 0 \\ & \left.1, g(i)+1, \frac{1}{g(i)+1}, \frac{1}{(g(i)+1)^{2}}, h(i), 0,0,0,0 \quad\right] \end{aligned}$$

여기서 $g(i)=\left\lfloor\frac{-1+\sqrt{1+8 i}}{2}\right\rfloor$ 이고 $h(i)=g(i+1)-g(i)$ 이다. $h(i)$는 이진 지시 변수(binary indicator variable) $1\left\{\frac{-1+\sqrt{1+8 i}}{2}=\left\lfloor\frac{-1+\sqrt{1+8 i}}{2}\right\rfloor\right\}$로 축소된다는 점에 유의하라.

Induction Setup

다음으로, 출력 시퀀스 $\boldsymbol{y}_{1}, \boldsymbol{y}_{2}, \ldots$를 생성하기 위한 decoder layer를 구성하는 방법을 보여준다. 여기서 $\boldsymbol{y}_{i}$는 다음과 같이 주어진다:

$$\begin{aligned} \boldsymbol{y}_{i}=[ & \llbracket q^{g(i)} \rrbracket, \llbracket s^{g(i)} \rrbracket, c^{g(i)} \\ & 0, \ldots, 0 \\ & \mathbf{0}_{s}, 0, \llbracket w^{(i)} \rrbracket \\ & \left.0,0,0,0,0, u_{1}^{(i)}, u_{2}^{(i)}, u_{3}^{(i)}, u_{4}^{(i)} \quad\right] \end{aligned}$$

즉, **sparse decoder의 $i$번째 스텝 $\boldsymbol{y}_{i}$**는 시간 $g(i)$에서의 Turing machine $M$의 상태, 시간 $g(i)$에서의 $M$의 헤드 아래 기호, 그리고 시간 $g(i)$에서의 $M$의 헤드 현재 위치에 대한 정보를 포함할 것이다. 또한, **placeholder 기호 $w$와 placeholder scalar $u_{1}, u_{2}, u_{3}$**가 있으며, 이들의 역할은 구성 과정에서 명확해질 것이다.

decoder의 시작 벡터는 다음과 같다:

$$\begin{aligned} \boldsymbol{y}_{1}=[ & \llbracket q_{\text {init }} \rrbracket, \llbracket \# \rrbracket, 0, \\ & 0, \ldots, 0, \\ & 0, \ldots, 0, \\ & 0, \ldots, 0 \end{aligned}$$

우리는 시작 헤드가 $c^{(0)}=0$에 있고, 초기 상태는 $q^{(0)}=q_{\text {init}}$이며, 깨끗한 테이프에서 초기화하므로 $s^{(0)}=\#$라고 가정한다. 우리는 귀납적 논증을 통해 우리 구성의 정확성을 보여줄 것이다: 아키텍처를 부분별로 설명하고, 동시에 모든 $r \geq 0$에 대해 우리 아키텍처가 이전 벡터들 $\left(\boldsymbol{y}_{0}, \ldots, \boldsymbol{y}_{r}\right)$로부터 $\boldsymbol{y}_{r+1}$을 어떻게 구성하는지를 보여줄 것이다. 따라서, $\boldsymbol{y}_{1}, \ldots, \boldsymbol{y}_{r}$이 위에서 언급된 속성들을 만족한다고 가정하자. Positional encoding을 사용하고 있으므로, decoder의 첫 번째 layer에 대한 실제 입력은 다음 시퀀스이다:

$$\boldsymbol{y}_{1}+\operatorname{pos}_{\mathrm{Dec}}(1), \boldsymbol{y}_{2}+\operatorname{pos}_{\mathrm{Dec}}(2), \ldots, \boldsymbol{y}_{r}+\operatorname{pos}_{\mathrm{Dec}}(r)$$

우리는 벡터 $\boldsymbol{y}_{i}$에 positional encoding이 더해진 벡터를 $\overline{\boldsymbol{y}}_{i}$로 표기한다. 따라서 모든 $1 \leq i \leq r$에 대해 다음이 성립한다:

$$\begin{aligned} \overline{\boldsymbol{y}}_{i}=[ & \llbracket q^{g(i)} \rrbracket, \llbracket s^{g(i)} \rrbracket, c^{g(i)} \\ & 0, \ldots, 0 \\ & \mathbf{0}_{s}, 0, \llbracket w^{(i)} \rrbracket \\ & \left.1, g(i)+1, \frac{1}{g(i)+1}, \frac{1}{(g(i)+1)^{2}}, h(i), u_{1}^{(i)}, u_{2}^{(i)}, u_{3}^{(i)}, u_{4}^{(i)} \quad\right] \end{aligned}$$

B.2.1 Layer 1: Simulate Transition Function

이 layer에서는 encoder와 decoder 간의 cross-attention을 사용하여 입력 문자열에 접근하고, feed-forward network를 사용하여 $M$의 전이 함수(transition function)를 시뮬레이션한다. Eq. (5)의 첫 번째 self-attention은 이 layer에서 사용되지 않으며, 우리는 단순히 **항등 함수(identity function)**를 생성한다. 이 항등 함수는 모든 query, key, value를 0으로 설정하고 residual connection을 추가함으로써 달성된다. 따라서 $\boldsymbol{p}_{i}^{1}=\overline{\boldsymbol{y}}_{i}$가 된다.

$\boldsymbol{p}_{i}^{1}$이 $[\ldots, \ldots, \ldots, 1, g(i)+1, \qquad, \ldots,]$ 형태이므로, Pérez et al. [72]의 Lemma B.1에 따라 $\boldsymbol{p}_{i}^{1}$을 사용하여 encoder에 attend하면 다음을 얻는다:

$$\begin{aligned} \operatorname{CrossAttN}\left(\boldsymbol{p}_{i}^{1}, \boldsymbol{K}^{\mathbf{e}}, \boldsymbol{V}^{\mathbf{e}}\right)=\left[\begin{array}{l} 0, \ldots, 0 \\ 0, \ldots, 0 \\ \\ \llbracket \alpha^{g(i)+1} \rrbracket, \beta^{g(i)+1}, \mathbf{0}_{s} \\ 0, \ldots, 0 \end{array}\right] \end{aligned}$$

여기서 $\alpha$와 $\beta$는 [72]의 Eq. (21)에 정의된 바와 같다. 따라서 Eq. [4]에서 우리는 최종적으로 다음으로 주어지는 벡터 $\boldsymbol{a}_{i}^{1}$을 생성한다:

$$\begin{aligned} \boldsymbol{a}_{i}^{1}= & \operatorname{CrOSSATTN}\left(\boldsymbol{p}_{i}^{1}, \boldsymbol{K}^{\mathbf{e}}, \boldsymbol{V}^{\mathbf{e}}\right)+\boldsymbol{p}_{i}^{1} \\ = & {\left[\begin{array}{l} \llbracket q^{g(i)} \rrbracket, \llbracket s^{g(i)} \rrbracket, c^{g(i)} \\ 0, \ldots, 0 \end{array}\right.} \\ & \llbracket \alpha^{g(i)+1} \rrbracket, \beta^{g(i)+1}, \llbracket w^{(i)} \rrbracket \\ & \left.1, g(i)+1, \frac{1}{g(i)+1}, \frac{1}{(g(i)+1)^{2}}, h(i), u_{1}^{(i)}, u_{2}^{(i)}, u_{3}^{(i)}, u_{4}^{(i)} \quad\right] \end{aligned}$$

첫 번째 decoder layer의 마지막 부분으로, 다음 Lemma를 만족하는 함수 $O_{1}(\cdot)$ (Eq. (3))을 사용한다. Lemma 6 (Lemma B.2 [72]). 두 개의 layer로 구성된 feed-forward network $O_{1}: \mathbb{Q}^{d} \rightarrow \mathbb{Q}^{d}$가 존재하여, 입력 벡터 $\boldsymbol{a}_{i}^{1}$ (Eq. (7))에 대해 다음을 출력으로 생성한다:

$$\left.\begin{array}{rl} O_{1}\left(\boldsymbol{a}_{i}^{1}\right)=[ & 0, \ldots, 0 \\ & \llbracket q^{g(i)+1} \rrbracket, \llbracket v^{g(i)} \rrbracket, m^{g(i)}, 0,0,0,0 \\ & 0, \ldots, 0 \\ & 0, \ldots, 0 \end{array}\right]$$

즉, 함수 $O_{1}(\cdot)$은 전이 $\delta\left(q^{g(i)}, s^{g(i)}\right)$를 시뮬레이션하여 $\llbracket q^{g(i)+1} \rrbracket, \llbracket v^{g(i)} \rrbracket$, 그리고 $m^{g(i)}$를 구성하며, 이 외에 몇 가지 다른 선형 변환을 수행한다.

따라서, 최종적으로 첫 번째 decoder layer의 출력은 다음과 같다:

$$\begin{aligned} \boldsymbol{z}_{i}^{1}=O_{1}\left(\boldsymbol{a}_{i}^{1}\right)+\boldsymbol{a}_{i}^{1}=[ & \llbracket q^{g(i)} \rrbracket, \llbracket s^{g(i)} \rrbracket, c^{g(i)}, \\ & \llbracket q^{g(i)+1} \rrbracket, \llbracket v^{g(i)} \rrbracket, m^{g(i)}, 0,0,0,0, \\ & \llbracket \alpha^{g(i)+1} \rrbracket, \beta^{g(i)+1}, \llbracket w^{(i)} \rrbracket, \\ & \left.1, g(i)+1, \frac{1}{g(i)+1}, \frac{1}{(g(i)+1)^{2}}, h(i), u_{1}^{(i)}, u_{2}^{(i)}, u_{3}^{(i)}, u_{4}^{(i)} \quad\right] \end{aligned}$$

B.2.2 Layer 2: Finding Head Node

이 layer에서는 feed-forward network만을 사용하여 head의 다음 위치를 평가한다. self-attention과 cross-attention은 identity function으로 설정되므로, $\boldsymbol{a}_{i}^{2}=\boldsymbol{p}_{i}^{2}=\boldsymbol{z}_{i}^{1}$이다.
$c^{g(i)}$는 시간 $g(i)$에 $M$이 가리키는 cell이며, 다음 재귀 관계를 만족한다: $c^{g(i)+1}=c^{g(i)}+m^{g(i)}$. 이를 확장하면 $c^{g(i)+1}=m^{(0)}+m^{(1)}+\cdots+m^{g(i)}$임을 알 수 있다.
비선형성을 가진 두 개의 layer network가 $c^{g(i)}, m^{g(i)}$, 그리고 $1 /(g(i)+1)$로부터 $c^{g(i)+1} /(g(i)+1)$와 $c^{g(i)} /(g(i)+1)$를 계산할 수 있다는 것은 어렵지 않게 알 수 있다. 이는 $c^{g(i)+1}=c^{g(i)}+m^{g(i)}$ 관계를 이용한다.
Layer 2의 끝에서 우리는 다음을 얻는다:

$$\begin{aligned} \boldsymbol{z}_{i}^{2}=O_{2}\left(\boldsymbol{a}_{i}^{2}\right)+\boldsymbol{a}_{i}^{2}=[ & \llbracket q^{g(i)} \rrbracket, \llbracket s^{g(i)} \rrbracket, c^{g(i)}, \\ & \llbracket q^{g(i)+1} \rrbracket, \llbracket v^{g(i)} \rrbracket, c^{g(i)+1}, \frac{1}{g(i)+1}, \frac{1}{(g(i)+1)^{2}}, \frac{c^{g(i)+1}}{g(i)+1}, \frac{c^{g(i)}}{g(i)+1}, \\ & \llbracket \alpha^{g(i)+1} \rrbracket, \beta^{g(i)+1}, \llbracket w^{(i)} \rrbracket, \\ & 1, g(i)+1, \frac{1}{g(i)+1}, \frac{1}{(g(i)+1)^{2}}, h(i), u_{1}^{(i)}, u_{2}^{(i)}, u_{3}^{(i)}, u_{4}^{(i)} \end{aligned}$$

B.2.3 Layer 3: Distinguishing Node Type

이것은 희소 그래프(sparse graph)에서 연산을 전파하는 추가적인 layer이다 ([72]의 연구에는 존재하지 않음). 특히, 우리는 이 layer를 사용하여 중간 노드(intermediate node)에서 상태를 "계산"하거나 누적할 것이다. 아래에서 이를 명확히 설명한다.
self-attention과 cross-attention은 모두 항등 함수(identity function)로 설정되어 $\boldsymbol{a}_{i}^{3}=\boldsymbol{p}_{i}^{3}=\boldsymbol{z}_{i}^{2}$이다. 이 layer에서는 새롭게 계산된 상태를 선택하거나 이전 상태를 계속 유지하기 위해 dense attention layer만 사용한다. [72]의 Lemma B.6과 유사한 아이디어를 사용하여, 다음과 같은 dense network를 구성할 수 있다:

$$O([\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}, b]))= \begin{cases}{[\mathbf{0}, \mathbf{0}, \mathbf{0}, 0]} & \text { if } b=1 \\ {[\mathbf{0}, \boldsymbol{z}-\boldsymbol{y},-\boldsymbol{z}, 0]} & \text { if } b=0\end{cases}$$

음수 값은 skip connection의 결과를 상쇄하기 위해 생성된다. 우리는 이러한 네트워크를 활용하여 중간 단계(intermediate steps)의 Turing machine 상태와 position embedding을 이전 시간 단계에서 받은 값으로 전환하고, compute node에 대해서는 아무것도 하지 않는다.
우리는 $h(i)$를 flipping bit $b$로 사용한다. 따라서 layer 3의 끝에서 우리는 다음을 얻는다:

$$\begin{aligned} \boldsymbol{z}_{i}^{3}=O_{3}\left(\boldsymbol{a}_{i}^{3}\right)+\boldsymbol{a}_{i}^{3}=[ & 0, \ldots, 0 \\ & \llbracket \hat{q}^{(i)} \rrbracket, \llbracket \hat{v}^{(i)} \rrbracket, \hat{c}^{(i)}, \frac{1}{g(i)+1}, \frac{1}{(g(i)+1)^{2}}, \frac{c^{g(i)+1}}{g(i)+1}, \hat{u}_{4}^{(i)} \\ & \llbracket \hat{\alpha}^{(i)} \rrbracket, \hat{\beta}^{(i)}, \mathbf{0}_{s} \\ & 1, \hat{u}_{1}^{(i)}, \hat{u}_{2}^{(i)}, \hat{u}_{3}^{(i)}, h(i), 0,0,0,0 \end{aligned}$$

여기서 우리는 이전 상태를 선택하기 위해 $h(i)$를 사용했다. 특히,

• 중간 노드(intermediate node)의 경우 입력 상태와 head position을 그대로 복사한다. 이 노드에서는 다음 Turing machine 상태로 전환할 필요가 없다.

$$\hat{q}^{(i)}=\left\{\begin{array}{ll} q^{g(i)+1} & \text { if } h(i)=1 \\ q^{g(i)} & \text { if } h(i)=0 \end{array}, \quad \hat{v}^{(i)}=\left\{\begin{array}{ll} v^{g(i)} & \text { if } h(i)=1 \\ w^{(i)} & \text { if } h(i)=0 \end{array}, \quad \hat{c}^{(i)}=\left\{\begin{array}{ll} c^{g(i)+1} & \text { if } h(i)=1 \\ c^{g(i)} & \text { if } h(i)=0 \end{array} .\right.\right.\right.$$

• 중간 노드에서 head 아래의 symbol을 보존하기 위해, 이전 symbol을 $\alpha$ 위치로 복사하고 $\beta=g(i)+1$로 설정한다. 이는 $\beta=g(i)+1$일 경우, 최종 변환 layer에 의해 $\alpha$ 위치의 symbol이 다음 Transformer 단계의 head 아래 symbol로 복사되기 때문이다. 따라서 Turing machine이 이 노드들을 전환하지 않으므로, 이전 head 아래 symbol을 올바르게 보존한다. compute node의 경우 평소와 같이 작동한다.

$$\hat{\alpha}^{(i)}=\left\{\begin{array}{ll} \alpha^{g(i)+1} & \text { if } h(i)=1 \\ s^{g(i)} & \text { if } h(i)=0 \end{array}, \quad \hat{\beta}^{(i)}=\left\{\begin{array}{ll} \beta^{g(i)+1} & \text { if } h(i)=1 \\ g(i)+1 & \text { if } h(i)=0 \end{array} .\right.\right.$$

• 마지막으로 중간 노드의 경우, 현재 가장 좋은 symbol $w$에 해당하는 position embedding을 복사하며, 이는 $u_{1}, u_{2}, u_{3}$에 저장된다. compute node의 경우, position embedding은 현재 Turing machine 단계에 해당하도록 한다.

$$\begin{array}{ll} \hat{u}_{1}^{(i)}=\left\{\begin{array}{ll} g(i)+1 & \text { if } h(i)=1 \\ u_{1}^{(i)} & \text { if } h(i)=0 \end{array},\right. & \hat{u}_{2}^{(i)}=\left\{\begin{array}{ll} \frac{1}{(g(i)+1)} & \text { if } h(i)=1 \\ u_{2}^{(i)} & \text { if } h(i)=0 \end{array},\right. \\ \hat{u}_{3}^{(i)}=\left\{\begin{array}{ll} \frac{1}{(g(i)+1)^{2}} & \text { if } h(i)=1 \\ u_{3}^{(i)} & \text { if } h(i)=0 \end{array},\right. & \hat{u}_{4}^{(i)}=\left\{\begin{array}{ll} \frac{c^{g(i)}}{g(i)+1} & \text { if } h(i)=1 \\ u_{4}^{(i)} & \text { if } h(i)=0 \end{array} .\right. \end{array}$$

추가적인 단순화를 위해, $h(i)=0$이면 $g(i+1)=g(i)$이고, $h(i)=1$이면 $g(i)+1$이 된다는 점에 주목한다. 이 사실을 통해 $\hat{q}^{(i)}=q^{g(i+1)}$ 및 $\hat{c}^{(i)}=c^{g(i+1)}$임을 결론 내릴 수 있다. 따라서 다음과 같이 쓸 수 있다:

$$\begin{aligned} \boldsymbol{z}_{i}^{3}=[ & 0, \ldots, 0, \\ & \llbracket q^{g(i+1)} \rrbracket, \llbracket \hat{v}^{(i)} \rrbracket, c^{g(i+1)}, \frac{1}{g(i)+1}, \frac{1}{(g(i)+1)^{2}}, \frac{c^{g(i)+1}}{g(i)+1}, \hat{u}_{4}^{(i)}, \\ & \llbracket \hat{\alpha}^{(i)} \rrbracket, \hat{\beta}^{(i)}, \mathbf{0}_{s}, \\ & 1, \hat{u}_{1}^{(i)}, \hat{u}_{2}^{(i)}, \hat{u}_{3}^{(i)}, h(i), 0,0,0,0 \end{aligned}$$

B.2.4 Layer 4: Finding next symbol on tape

다음 head position $c^{g(i)+1}$ 아래의 tape에서 symbol을 찾기 위해, 우리는 위치 $c^{g(i)+1}$에 마지막으로 무엇이 쓰여졌는지 찾으려고 한다. 이를 용이하게 하기 위해, [72]를 따라 우리는 $\ell(j)$를 $M$이 위치 $c^{(j)}$를 가리켰던 마지막 시간( $j$ 이전)으로 정의하거나, $M$이 $c^{(j)}$를 처음 가리키는 경우 $j-1$로 정의한다. 여기서 $j$는 Turing machine step counter이며, sparse Transformer step $i$와는 다르다. [72]는 full attention mechanism을 활용하여 $v^{\ell(j+1)}$를 한 번에 찾을 수 있었지만, 우리는 sparse attention mechanism 때문에 여러 단계에 걸쳐 이를 수행해야 한다. 우리는 [72]에서 full attention에 사용된 것과 유사한 query, key, value 함수를 모든 $i$에 대해 사용한다:

$$\begin{aligned} Q_{4}\left(\boldsymbol{z}_{i}^{3}\right)=[\quad & 0, \ldots, 0 \\ & 0, \ldots, 0 \\ & 0, \ldots, 0 \\ & \left.0, \frac{c^{g(i)+1}}{g(i)+1}, \frac{1}{g(i)+1}, \frac{1}{3(g(i)+1)^{2}}, 0,0,0,0,0 \quad\right] \end{aligned}$$ $$\begin{aligned} & K_{4}\left(\boldsymbol{z}_{i}^{3}\right)=[\quad 0, \ldots, 0 \\ & 0, \ldots, 0 \\ & 0, \ldots, 0 \\ & V_{4}\left(\boldsymbol{z}_{i}^{3}\right)=\left[\begin{array}{l} 0, \hat{u}_{2}^{(i)}, \hat{u}_{4}^{(i)}, \hat{u}_{3}^{(i)}, 0,0,0,0,0 \\ 0, \ldots, 0 \\ 0, \ldots, 0 \\ \mathbf{0}_{s}, 0, \llbracket \hat{v}^{(i)} \rrbracket \\ 0,0,0,0,0, \hat{u}_{1}^{(i)}, \hat{u}_{2}^{(i)}, \hat{u}_{3}^{(i)}, \hat{u}_{4}^{(i)} \end{array}\right] \end{aligned}$$

세 함수가 선형 변환이므로 feedforward network로 정의될 수 있음은 분명하다. query vector는 항상 현재 time step position embedding을 사용하여 형성되는 반면, key 및 value vector는 중간 노드에 대해 복사된 항목을 사용하고 compute node에 대해서만 현재 항목을 사용하여 형성된다는 점에 주목하라. Pérez et al. [72]는 원하는 $v^{l(j+1)}$를 full attention을 사용하여 $v^{m(j)}$로 찾는데, 여기서

$$m(t)=\underset{m \in\{0, \ldots, t\}}{\arg \min } \chi_{t}^{j}=\underset{m \in\{0, \ldots, t\}}{\arg \min }\left|\left\langle Q_{4}\left(\boldsymbol{z}_{j}^{3}\right), K_{4}\left(\boldsymbol{z}_{m}^{3}\right)\right\rangle\right|$$

최소화는 Turing machine step, 즉 우리 경우 compute node에 대해서만 이루어진다. 우리는 sparse attention mechanism을 사용하여 $m(j)$를 부분적으로 추정할 수 있음을 아래에서 보여준다. 주요 아이디어는 최소화 문제 $\min _{m \in\{0, \ldots, t\}} \chi_{t}^{j}$가 결합 법칙에 의해 $\min \left\{\cdots \min \left\{\min \left\{\chi_{0}^{j}, \chi_{1}^{j}\right\}, \chi_{2}^{j}\right\}, \ldots, \chi_{t}^{j}\right\}$로 표현될 수 있다는 점을 주목하는 것이다. 우리 그래프 $D$의 정의에 따르면, $j(j+1) / 2+k$ 형태의 모든 중간 노드 $i$, 즉 $k>0, g(i)=j$ 및 $h(i)=0$인 경우, 우리는 노드 $k(k+1) / 2$와 $i-1$에서 지금까지 복사된 최적의 값에 attend할 것이다. 노드 $k(k+1) / 2$는 모든 $k$에 대해 $h(k(k+1) / 2)=1$이므로 중간 노드가 아니며, 사실 Turing machine의 step $k$에 해당한다. 이는 노드 $k(k+1) / 2$와 $i-1$ 사이의 최소값에 해당하는 key와 value를 선택하는 데 도움이 될 것이다. 다시 말해, $j(j+1) / 2+k$ 형태의 노드 $i$에서 우리는 $m(k)$와 해당 선택된 값을 평가했을 것이다:

$$w^{(j(j+1) / 2+k+1)}=\hat{v}^{m(k-1)}$$

그리고 $u$에 대해서도 마찬가지이다. 따라서 모든 중간 노드를 거친 후, 마침내 다음 compute node, 즉 $k=j+1$일 때, 우리는 $0,1, \ldots, j$ 전체에 대한 최소값을 얻을 것이다. 이는 compute node에서 $\ell(g(i)+1)$과 그에 해당하는 값을 [72]의 Lemma B.4에 표시된 대로 복구할 수 있음을 의미한다. 그러면 $\boldsymbol{p}_{i}^{4}$는 다음과 같이 주어진다:

$$\begin{aligned} \boldsymbol{p}_{i}^{4}= & \operatorname{ATTN}_{D}\left(\boldsymbol{Z}_{i}^{3}\right)+\boldsymbol{z}_{i}^{3} \\ = & 0, \ldots, 0 \\ & \llbracket q^{g(i+1)} \rrbracket, \llbracket \hat{v}^{(i)} \rrbracket, c^{g(i+1)}, 0, \frac{c^{g(i)+1}}{g(i)+1}, \hat{u}_{4}^{(i)} \\ & \llbracket \hat{\alpha}^{(i)} \rrbracket, \hat{\beta}^{(i)}, \llbracket w^{(i+1)} \rrbracket \\ & \left.1, \hat{u}_{1}^{(i)}, \hat{u}_{2}^{(i)}, \hat{u}_{3}^{(i)}, h(i), u_{1}^{(i+1)}, u_{2}^{(i+1)}, u_{3}^{(i+1)}, u_{4}^{(i+1)} \quad\right] \end{aligned}$$

cross-attention과 feed-forward network는 identity로 설정되므로, $\boldsymbol{z}_{i}^{4}=\boldsymbol{a}_{i}^{4}=\boldsymbol{p}_{i}^{4}$이다.

B.2.5 Final transformation

우리는 Pérez et al. [72]의 해당 lemma에서 제시된 최종 변환 함수 $F(\cdot)$를 약간 수정하여 구성을 마무리한다.

Lemma 7 (Lemma B. 5 [72]). feed-forward network로 정의되는 함수 $F: \mathbb{Q}^{d} \rightarrow \mathbb{Q}^{d}$가 존재하며, 다음을 만족한다:

$$\begin{aligned} F\left(\boldsymbol{z}_{r}^{4}\right)= & {\left[\begin{array}{l} \llbracket q^{g(r+1)} \rrbracket, \llbracket s^{g(r+1))} \rrbracket, c^{g(r+1)} \\ 0, \ldots, 0 \end{array}\right.} \\ & \mathbf{0}_{s}, 0, \llbracket w^{(r+1)} \rrbracket \\ =\quad & \left.0,0,0,0,0, u_{1}^{(r+1)}, u_{2}^{(r+1)}, u_{3}^{(r+1)}, u_{4}^{(r+1)}\right] \\ & \boldsymbol{y}_{r+1} \end{aligned}$$

수정 사항은 $w, u_1, u_2, u_3$가 통과하도록 하는 것이다. 이는 다음 time step에서 intermediate node와 compute node 모두에 대해 Transformer의 원하는 입력을 제공하며, 이로써 우리의 귀납법이 결론에 이른다.

C Limitations

마지막으로, 우리는 sparse attention 메커니즘이 dense attention 메커니즘을 보편적으로 대체할 수 없다는 것, 즉 **"공짜 점심은 없다(no free lunch)"**는 것을 보여준다. 우리는 full attention 메커니즘이 $O(1)$ layer 내에서 해결할 수 있는 자연스러운 task를 제시한다. 그러나 표준 복잡도 이론적 가정 하에, 이 문제는 $\tilde{O}(n)$ 개의 edge를 가진 어떤 sparse attention layer (단순히 BIGBIRD뿐만 아니라)에 대해서도 $\tilde{\Omega}(n)$ layer가 필요하다는 것을 보인다. (여기서 $\tilde{\Omega}(n)$은 poly-logarithmic factor에 대한 의존성을 숨기는 표준 표기법이다.)

우리는 길이 $n$이고 차원 $d \in \Omega\left(\log ^{2} n\right)$인 주어진 시퀀스에서 각 벡터에 대해 가장 먼 벡터를 찾는 간단한 문제를 고려한다. 차원에 대한 가정은 완화된 것으로, 많은 상황에서 차원 $d=768$은 실제 $n$의 수와 비교할 만하다. Task 1. $\mathbb{R}^{d}$에 있는 $n$개의 단위 벡터 $\left\{u_{1}, \ldots, u_{n}\right\}$ (여기서 $d=\Theta\left(\log ^{2} n\right)$)가 주어졌을 때, $f\left(u_{1}, \ldots, u_{n}\right) \rightarrow\left(u_{1^{*}}, \ldots, u_{n^{*}}\right)$를 계산한다. 여기서 고정된 $j \in[n]$에 대해 $j^{*}=\arg \max _{k}\left\|u_{k}-u_{j}\right\|_{2}^{2}$로 정의한다.

가장 멀리 떨어진 벡터를 찾는 것은 단위 벡터의 경우 내적(inner product) 검색을 최소화하는 문제로 귀결된다. 적절한 query와 key를 가진 full-attention 메커니즘의 경우, 모든 쌍별 내적을 평가할 수 있으므로 이 task는 매우 쉽다. sparse-attention에 대한 불가능성은 Orthogonal Vector Conjecture (OVC) [2, 1, 96, 7]에서 비롯된 난이도 결과에서 기인하며, 이는 fine-grained complexity에서 널리 사용되는 가정이다. 비공식적으로, OVC는 $n$개의 Boolean 벡터들 사이에서 최소 내적이 0인지 여부를 subquadratic 시간 내에 결정할 수 없다고 명시한다. Conjecture 1 (Orthogonal Vectors Conjecture). 모든 $\epsilon>0$에 대해 $c \geq 1$이 존재하여, $d$ 차원의 $n$개 Boolean 벡터가 주어졌을 때, $d \geq c \log n$인 인스턴스에서 $O\left(n^{2-\epsilon}\right)$ 시간 내에 직교 벡터 쌍이 존재하는지 여부를 결정할 수 없다.

Conjecture 1을 사용하여, 우리는 Task 1을 완료하는 어떤 sparse directed graph $D$를 가진 Transformer $g \in \mathcal{T}_{D}^{H=O(d), m=O(d), q=O(d)}$가 superlinear한 수의 layer를 필요로 함을 보이기 위한 환원(reduction)을 제시한다. Proposition 2. Task 1을 평가할 수 있는 단일 layer full-attention 네트워크 $g \in \mathcal{T}^{H=1, m=2 d, q=0}$가 존재한다. 즉, $g\left(u_{1}, \ldots, u_{n}\right)=\left[u_{1} *, \ldots, u_{n} *\right]$이다. 그러나 $\tilde{O}(n)$개의 edge (즉, 내적 평가)를 가진 그래프 $D$를 가진 $\mathcal{T}_{D}^{H=O(d), m=O(d), q=O(d)}$의 어떤 sparse-attention 네트워크는 $\tilde{\Omega}\left(n^{1-o(1)}\right)$ layer를 필요로 할 것이다.

증명. 이 증명은 두 부분으로 나뉜다:

Part 1: Full attention 메커니즘은 $O(1)$ layer 내에서 문제를 해결할 수 있다. 우리는 Task 1을 평가할 수 있는 단일 layer full self-attention의 명시적인 구성을 제공하는 것으로 시작한다. Step 1. 입력의 각 $u_{i}$를 다음과 같이 $\mathbb{R}^{2 d}$에 임베딩한다:

$$x_{i}:=E\left(u_{i}\right)=\left[u_{i} ; 0\right]$$

Step 2. query, key, value 함수를 다음과 같이 구성한다:

$$\begin{aligned} Q([a ; b]) & =-a \\ K([a ; b]) & =a \\ V([a ; b]) & =[0 ; a] \end{aligned}$$

그러면 $\operatorname{Attn}\left(Q\left(x_{i}\right), K(X), V(X)=\left[0 ; u_{\arg \max _{j}\left\langle-u_{i}, u_{j}\right\rangle}\right]\right.$이다. 이어서,

$$a_{i}=\operatorname{Attn}\left(Q\left(x_{i}\right), K(X), V(X)\right)+x_{i}=\left[u_{i} ; u_{\arg \max _{j}\left\langle-u_{i}, u_{j}\right\rangle}\right]=\left[u_{i} ; u_{i^{*}}\right]$$

Step 3. $O\left(a_{i}\right)=0$이라고 하면, 출력 $z_{i}=\left[u_{i} ; u_{i^{*}}\right]$는 우리가 원하는 바와 같다. 논증을 완성하기 위해, 이제 $\left\langle u_{i}, u_{i^{*}}\right\rangle$만 비교하면 되므로 직교 벡터 쌍이 있는지 확인하는 데 $O(n)$개의 내적만 필요하다는 점을 관찰한다.

Part 2: 모든 Sparse Attention 메커니즘은 $\tilde{\Omega}\left(n^{1-\epsilon}\right)$ layer를 필요로 할 것이다. 우리는 $\tilde{O}(n)$개의 edge를 가진 sparse-attention 그래프 $D$를 가진 어떤 $g \in \mathcal{T}_{D}^{H=O(d), m=O(d), q=O(d)}$ 네트워크로 Task 1을 해결하는 것이 불가능하다는 것을 귀류법으로 증명한다. 만약 $l$개의 layer를 가진 네트워크 $g \in \mathcal{T}_{D}^{H=O(d), m=O(d), q=O(d)}$를 사용하여 Task 1을 해결할 수 있다고 가정하자. 한 layer에서 수행하는 모든 계산은 다음과 같다:

$$\begin{aligned} & a_{i}=\operatorname{ATTN}_{D}\left(Q\left(x_{i}\right), K\left(X_{N(i)}\right), V\left(X_{N(i)}\right)+x_{i}\right. \\ & x_{i}=O\left(a_{i}\right)+a_{i} \end{aligned}$$

여기서 $\operatorname{Attn}_{D}$는 eq. (AT)에 정의되어 있다. 따라서 layer당 총 계산량은 $\tilde{O}\left(n d^{3}\right)$이며, $l$개의 layer로 구성된 전체 네트워크의 경우 $\tilde{O}\left(n l d^{3}\right)$이다. 우리는 Task 1의 결과를 사용하여 직교 벡터(OV) 문제(Conjecture 1에 정의됨)를 선형 시간 내에 해결할 수 있다. 따라서 총체적으로, 우리는 OV의 어떤 인스턴스도 $\tilde{O}\left(n l d^{3}\right)$ 시간 내에 해결할 수 있을 것이다. 이제 만약 어떤 $\epsilon>0$에 대해 $l=O\left(n^{1-\epsilon}\right)$이고 $d=\Theta\left(\log ^{2} n\right)$이라면, 우리는 OV를 $\tilde{O}\left(n^{2-\epsilon}\right)$ 시간 내에 해결할 수 있게 되어 Conjecture 1에 모순된다. 그러므로 우리는 최소한 $\tilde{\Omega}\left(n^{1-o(1)}\right)$ layer가 필요하다.

D Implementation details

우리는 최신 하드웨어에 맞춰 코드를 최적화한다. GPU 및 TPU와 같은 하드웨어 가속기는 연속적인 바이트 블록을 한 번에 로드하는 coalesced memory operation에서 진정한 성능을 발휘한다. 따라서 sliding window나 random element query로 인해 발생하는 작고 산발적인 look-up은 효율적이지 않다. 우리는 이러한 문제를 **look-up을 "블록화(blockifying)"**함으로써 완화한다.

GPU/TPU와 희소성(Sparsity)
이상적으로는 Section 2에서 설명된 인접 행렬(adjacency matrix) $A$가 희소(sparse)하다면, 구현 속도를 높이는 데 충분할 것이라고 기대할 수 있다. 그러나 이러한 희소 행렬 곱셈은 GPU에서 효율적으로 구현될 수 없음이 잘 알려져 있다 [33, 102]. GPU는 수천 개의 코어가 병렬로 연산을 수행하므로, Section 2에서 언급된 희소 행렬 곱셈을 효율적으로 수행할 수 없다.

결과적으로 우리는 먼저 attention 패턴을 블록화할 것을 제안한다. 즉, query와 key의 집합을 함께 묶은 다음, 이 블록들에 대해 attention을 정의한다. 이 과정은 Figure 3에 제시된 예시를 통해 설명하는 것이 더 쉽다.
가령, 12개의 query 벡터와 12개의 key 벡터가 있다고 가정하자. 블록 크기를 2로 설정하면, query 행렬은 $12/2=6$개의 블록으로, key 행렬도 $12/2=6$개의 블록으로 분할된다. 그런 다음 BigBird의 세 가지 구성 요소는 이 블록 행렬에 대해 정의된다. 특히 세 가지 구성 요소는 다음과 같다:

1. Random attention: 각 query 블록은 $r$개의 random key 블록에 attend한다. Figure 3a에서는 블록 크기가 2일 때 $r=1$이다. 이는 크기가 2인 각 query 블록이 크기가 2인 하나의 key 블록에 무작위로 attend한다는 것을 의미한다.
2. Window local attention: 블록을 생성할 때, query 블록의 수와 key 블록의 수가 동일하도록 보장한다. 이는 블록 window attention을 정의하는 데 도움이 된다. 인덱스 $j$를 가진 모든 query 블록은 인덱스 $j-(w-1)/2$부터 $j+(w-1)/2$까지의 key 블록에 attend하며, key 블록 $j$도 포함한다. Figure 3b에서는 블록 크기가 2일 때 $w=3$이다. 이는 각 query 블록 $j$ (크기 2의 query들)가 key 블록 $j-1, j, j+1$에 attend한다는 것을 의미한다.
3. Global attention: Global attention은 Section 2에서 정의된 것과 동일하지만, 블록 단위로 계산한다. Figure 3c에서는 블록 크기가 2일 때 $g=1$이다. BIGBIRD-ITC의 경우, 이는 하나의 query 블록과 key 블록이 모든 블록에 attend한다는 것을 의미한다.

결과적으로 얻어지는 전체 attention 행렬은 Figure 3d에 나타나 있다.
불행히도, 임의의 query와 key 벡터 쌍을 곱하여 이 attention 점수를 단순히 계산하려고 하면 gather operation을 사용해야 하는데, 이는 비효율적이다.
window attention과 global attention을 자세히 살펴보면, gather operation을 사용하지 않고도 이러한 attention 점수를 계산할 수 있음을 알 수 있다.

Figure 3: BIGBIRD에서 사용되는 블록-어텐션 메커니즘의 구성 요소 (블록 크기 = 2). 이는 어텐션 행렬이 $2 \times 2$ 크기의 블록으로 분할됨을 의미한다. 이전의 모든 BigBird 파라미터는 각 블록을 하나의 단위로 하여 작동한다. 흰색은 어텐션이 없음을 나타낸다. (a) $r=1$인 random attention, (b) $w=3$인 sliding window attention, (c) $g=1$인 global attention. (d) 결합된 BigBird 모델.

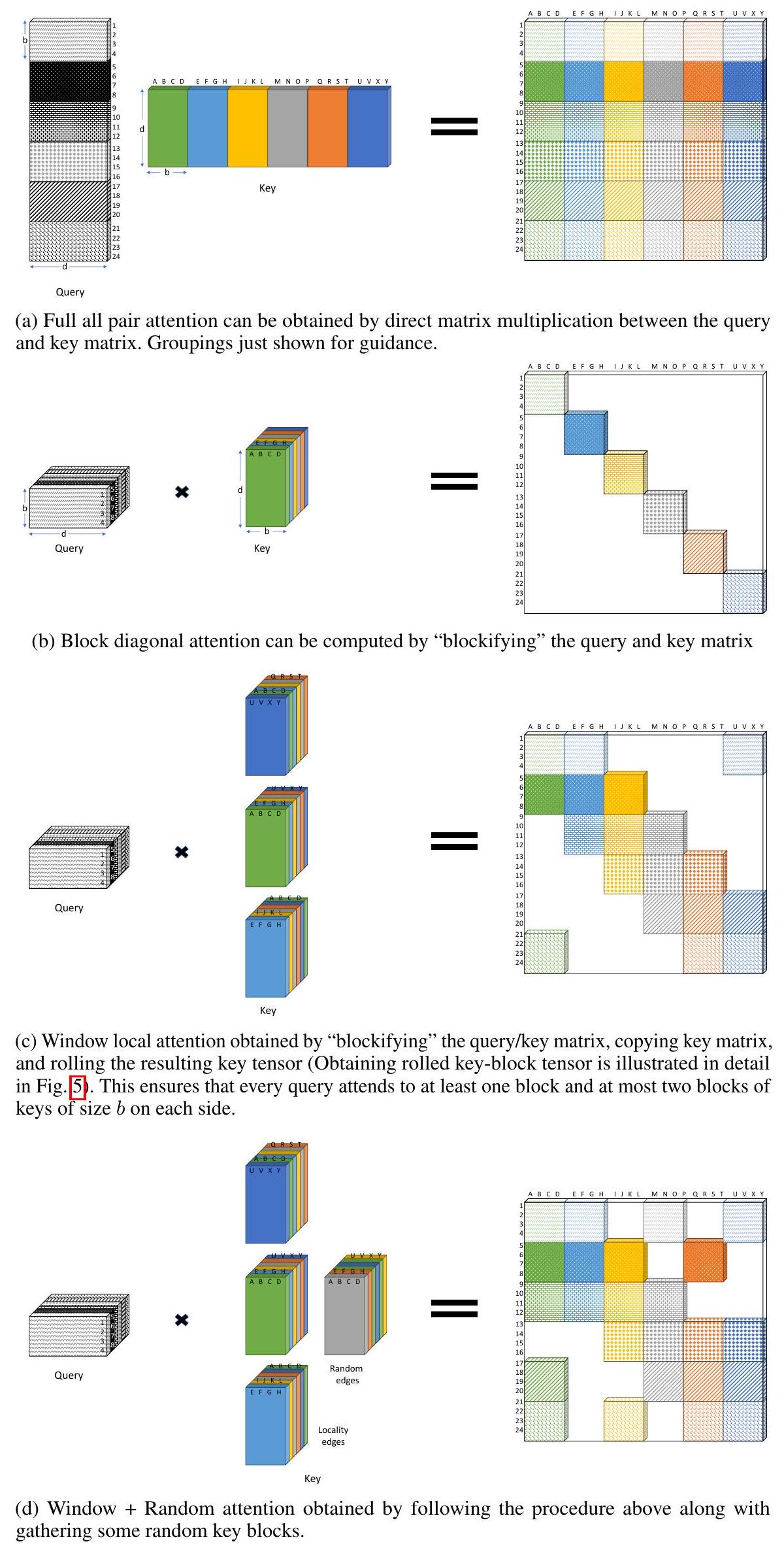
Figure 4: BIGBIRD의 빠른 희소 어텐션 계산 아이디어.

Figure 5: 롤링된 키-블록 텐서(rolled key-block tensor)의 구성. 키 행렬을 $w$개 복사한다. 복사본에 $-(w-1)/2 \leq j \leq (w-1)/2$로 인덱스를 부여한다. $j^{\text{th}}$ 복사본을 $j$ 블록만큼 롤링한다. 양의 롤링은 원형으로 엔트리를 왼쪽으로 이동시키는 것을 의미하며, 음의 롤링은 오른쪽으로 이동시키는 것에 해당한다. 마지막으로, 블록들을 새로운 축을 따라 그룹화하여 재구성함으로써 키-블록 텐서를 얻는다. 설명을 위해 $w=3$이 선택되었다.

전체 dense attention 점수는 Figure 4a에 나타난 바와 같이 $O(n^2 d)$의 비용으로 query 및 key 행렬의 간단한 행렬 곱셈으로 계산될 수 있음을 상기하자.
이제 query 및 key 행렬을 블록화하여 곱하면, Figure 4b에 묘사된 바와 같이 $O(nbd)$의 비용으로 attention 점수의 블록 대각선 부분을 얻을 수 있다.
이를 자세히 설명하기 위해, $n$개의 토큰에 해당하는 query 및 key 행렬을 $Q, K \in \mathbb{R}^{n \times d}$라고 가정하자. 여기서 $Q_{i.}=x_i W_Q$이고 $K_{i.}=x_i W_K$이다.
우리는 $n \times d$ 크기의 query 행렬 $Q$와 key 행렬 $K$를 시퀀스 길이를 따라 재구성하여 각각 $\lceil n/b \rceil \times b \times d$ 크기의 텐서 $Q'$와 $K'$를 얻는다. 이제 두 텐서를 다음과 같이 곱한다:

$$A_{j s t}=\sum_{u} Q_{j s u}^{\prime} K_{j t u}^{\prime}, \quad j=0,1, \ldots,\lceil n / b\rceil$$

결과로 얻어지는 $\lceil n/b \rceil \times b \times b$ 크기의 $A$ 텐서는 전체 attention 패턴의 블록 대각선 부분에 해당하도록 재구성될 수 있다.
이제 attention을 블록 대각선에서 window로 확장하기 위해, 즉 인덱스 $j$를 가진 query 블록이 인덱스 $j-(w-1)/2$부터 $j+(w-1)/2$까지의 key 블록에 attend하도록 하기 위해, 재구성된 key 텐서 $K'$를 $w$개 복사한다.
Figure 5에 나타난 바와 같이, **각 key-block 텐서 복사본을 $\lceil n/b \rceil$ 길이의 첫 번째 축을 따라 점진적으로 "롤링(roll)"**한다.
이 $w$개의 롤링된 key-block 텐서들을 query-block 텐서와 곱하면 원하는 window attention 점수를 얻을 수 있다 (Figure 4c).
마찬가지로 global component의 경우, global token에 해당하는 key 텐서의 첫 $g$개 블록을 항상 포함할 수 있다.
마지막으로, random attention은 매우 작기 때문에 (모든 실험에서 $r=3$), gather operation을 사용한다 (Figure 4d). 또한 설계상, 각 query 블록은 정확히 $r$개의 random 블록에 attend한다.

따라서 세 가지 구성 요소의 결과는 기본적으로 Figure 6에 나타난 바와 같이 **$\lceil n/b \rceil \times (g+w+r)b \times d$ 크기의 compact dense 텐서 $K''$**이다.
최종 attention 점수를 계산하는 것은 dense 텐서 곱셈으로 귀결되며, 이는 TPU/GPU에서 매우 효율적이다.
구체적으로, $Q'$ (크기: $\lceil n/b \rceil \times b \times d$)와 $K''$ (크기: $\lceil n/b \rceil \times (g+w+r)b \times d$)를 $O(n(g+w+r)bd)$의 비용으로 곱하여, $\lceil n/b \rceil \times b \times (g+w+r)b$ 크기의 원하는 attention 점수 텐서를 얻는다. 이 텐서는 BigBird 패턴에 따라 모든 attention 점수를 얻기 위해 재구성될 수 있다.

Figure 6: BIGBIRD 어텐션 계산 개요. **구조화된 블록 희소성(structured block sparsity)**은 희소 어텐션 연산을 압축적으로 패킹하는 데 도움을 주어, GPU/TPU에서 우리의 방법을 효율적으로 만든다. 왼쪽에는 변환된 dense query 및 key 텐서를 나타낸다. query 텐서는 단순히 블록화 및 재구성을 통해 얻어지는 반면, 최종 key 텐서는 세 가지 변환을 연결하여 얻어진다: global attention에 해당하는 첫 번째 녹색 열은 고정되어 있다. window local attention에 해당하는 중간 파란색 열은 Figure 5에 설명된 대로 적절한 롤링을 통해 얻을 수 있다. random attention에 해당하는 마지막 주황색 열의 경우, 계산적으로 비효율적인 gather operation을 사용해야 한다. query 및 key 텐서 간의 dense 곱셈은 Figure 4에 설명된 아이디어를 사용하여 희소 어텐션 패턴을 효율적으로 계산한다 (직접 곱셈으로 계산되는 첫 번째 행-블록 제외). 오른쪽의 결과 행렬은 Figure 3d에 나타난 것과 동일하다.

E NLP experiments details

E. 1 MLM Pretraining

우리는 BIGBIRD를 사전학습하기 위해 Books [110], CC-News [34], Stories [89], Wikipedia의 네 가지 공개 데이터셋을 사용한다. 어휘는 RoBERTa(GPT2에서 차용)와 동일한 sentencepiece vocabulary를 사용한다. 4096보다 긴 문서는 여러 문서로 분할하고, 4096보다 훨씬 작은 문서는 결합한다. 오리지널 BERT 학습 방식에 따라, 이 네 가지 데이터셋에서 토큰의 15%를 마스킹하고, 마스킹된 토큰을 예측하도록 학습한다. 우리는 RoBERTa의 체크포인트에서 warm start한다.
두 가지 다른 모델인 BigBird-ITC-base와 BigBird-ETC-base를 학습시켰다. 이 두 모델의 하이퍼파라미터는 Table 8에 제시되어 있다. 모든 실험에서 처음 10,000 스텝 동안 learning rate warmup을 사용하고, 이후 learning rate는 선형적으로 감소시켰다.
일반적인 관례에 따라, 우리는 24개 layer, 16개 head, hidden dimension 1024를 가진 대규모 모델 버전도 학습시켰다. RoBERTa의 관찰 결과에 따라, 이 규모의 모델에 대해서는 2048의 더 큰 batch size로 사전학습을 진행했다. BIGBIRD-ITC의 경우 block length는 base 모델과 동일하게 유지했지만, BIGBIRD-ETC의 경우 block length를 거의 두 배인 169로 늘렸다. 나머지 모든 파라미터는 동일하게 유지되었다.

Table 8: MLM을 위한 두 BigBird base 모델의 하이퍼파라미터.

E. 2 Question Answering

사용된 4개 데이터셋의 상세 통계는 Tab. 11에 제시되어 있다. Tab. 2를 생성하는 데 사용된 BigBird의 모든 하이퍼파라미터는 Tab. 12에, Tab. 3에 제출된 하이퍼파라미터는 Tab. 13에 나타나 있다. 우리는 학습 시 두 가지 유형의 regularization을 사용한다:

• contrastive predictive coding [70]의 변형을 dual encoder 모델로 사용했다.
• ITC에는 position embedding을, **ETC에는 relative position encoding [79]**을 사용한다.

다음으로, 데이터셋/task별 모델의 특징을 설명한다.

Table 9: 사전학습에 사용된 데이터셋.

Table 10: held-out 세트에서의 MLM 성능.

Table 11: Question Answering 데이터셋.

Table 12: Question Answering에 사용된 base BIGBIRD 모델의 하이퍼파라미터 (Tab. 2에 보고된 수치).

HotpotQA
데이터는 여러 개의 증거 단락과 각 질문으로 구성된다. 우리는 주어진 증거에 답이 없는 16개의 QA를 필터링했다. BigBird-ITC의 경우, 처음 128개의 global token을 사용한다. BigBird-ETC의 경우, 각 질문 토큰에 하나, 각 증거 단락에 하나, 그리고 단락 내 각 문장에 하나씩, 최대 256개의 global token을 사용한다. 증거 단락의 global token에 해당하는 출력에 dense layer를 사용하여 출력 logit에 대한 임계값을 통해 supporting fact인지 예측한다. 답변 유형(예/아니오/span)은 global CLS token에서 단일 dense layer로 예측된다. span 기반 답변의 경우, 시작 및 끝 위치 간의 거리가 30단어 이내가 되도록 시퀀스에 dense layer를 사용하여 span을 예측한다. span은 시작 및 끝 logit의 합으로 순위가 매겨진다.

Natural Questions
여기서도 데이터는 supporting evidence가 있는 질문으로 구성되지만, 여러 단락이 아닌 단일의 잠재적으로 긴 문서 형태이다. 우리는 [5]의 설정을 대체로 따른다. 4096보다 긴 문서의 경우, 2048의 stride를 가진 sliding window 접근 방식을 사용한다. 우리는 CLS token을 시작에, 이어서 질문, 이어서 구분자 토큰, 이어서 문서를 입력으로 사용한다. BigBird-ITC의 경우, 처음 128개의 토큰을 global로 만든다. BigBird-ETC의 경우, CLS, 질문, 그리고 각 단락에 대해 하나씩 global token을 만든다. 우리는 최종 layer에서 long answer start, long answer end, short answer start, short answer end를 각각 예측하기 위해 4개의 predictor를 학습시킨다. 답변의 시작과 끝을 독립적으로 예측하는 대신, 먼저 시작을 예측한 다음 시작 이후의 최적의 끝 위치를 예측한다. short answer의 경우, 시작과 끝 위치 간의 거리를 38단어 이내로 제한한다. 답변 유형(null, yes, no, short, long)은 CLS token 출력 embedding에서 예측된다. yes/no 답변에 대한 logit이 short, long 또는 null 답변에 대한 logit보다 높을 때, short answer를 해당 yes/no 텍스트로 대체한다.

TriviaQA
데이터는 Wikipedia 기사를 "noisy" supporting evidence로 하는 질문-답변 쌍으로 구성된다. 우리는 주어진 Wikipedia 기사에 답이 포함되어 있을 수도 있고 없을 수도 있기 때문에 이를 noisy하다고 부른다. 또한, 답변 엔티티는 기사 내 적절한 span으로 주석되어 있지 않고, fuzzy string matching을 사용하여 발견된 모든 발생이 나열된다. 우리는 CLS token을 시작에, 이어서 질문, 이어서 구분자 토큰, 이어서 문서를 입력으로 사용한다. BigBird-ITC의 경우, 처음 128개의 토큰을 global로 만든다. BigBird-ETC의 경우, CLS, 질문, 그리고 각 문장에 대해 하나씩 global token을 만들며, 최대 320개의 global token을 사용한다.

Table 13: 테스트를 위해 제출된 large BigBird 모델의 Question Answering 하이퍼파라미터 (Tab. 3에 보고된 수치).

답변 span의 noisy한 특성을 고려하여, 우리는 학습을 위해 Clark와 Gardner [18]를 따른다. 우리는 각 기사에 대해 답변 span을 독립적으로 예측하기 위해 시퀀스에 dense layer를 사용하며, 시작과 끝 위치 간의 거리는 16단어 이내로 제한한다. 각 기사에 대해 시작 logit + 끝 logit의 합이 최대인 span이 선택된다. 그런 다음 해당 질문과 관련된 모든 문서에 대해 정규화한다.

WikiHop
WikiHop의 각 질문에 대해 최대 79개의 후보와 63개의 supporting paragraph가 주어진다. BigBird-ITC 모델에서는 Beltagy et al. [8]을 따라, 답변과 질문을 특수 토큰인 [q] Question [/q] [ans] Ans1 [/ans] ... [ans] AnsN [/ans]과 함께 context에 연결한다. 텍스트의 시작이 항상 질문과 답변으로 이어지기 때문에, 처음 128개의 토큰이 전역적으로 attend하도록 한다. BigBird-ETC 모델에서는 global token을 적절하게 설계하므로 특수 토큰인 [ans], [/ans] 등을 삽입할 필요가 없다. 질문에 대한 global token과 함께, 각 후보 답변당 하나씩, 최대 430개의 global token을 사용한다. 또한, relative position label을 사용하여 답변 토큰을 해당 언급에 연결했다. 마지막으로, 후보 답변에 해당하는 출력 벡터를 입력으로 받아 현재 후보가 정답일 확률을 예측하는 dense layer를 사용한다. 이 dense layer를 각 후보에 독립적으로 적용하고, 가장 좋은 점수를 받은 후보가 최종 답변으로 선택된다.
ETC에서 명시적으로 설계된 attention 연결이 약간 더 잘 작동하지만, random 연결 기반의 ITC도 상당히 경쟁력이 있다는 점은 주목할 가치가 있다.

E. 3 Relationship to Contemporary Work

Longformer [16]는 연산량을 줄이기 위해 localized sliding window를 도입했다. localized sliding window와 global token을 포함하는 더 최신 버전은 Longformer [8]에 의해 독립적으로 소개되었다. BigBird는 추가적인 random token을 포함하지만, global token과 local token을 구현하는 방식에도 차이가 있다. 특히, question answering에서 SoTA를 달성하기 위해 random token을 사용하지 않는 경우에도 Longformer와 BigBird-etc 사이에는 두 가지 주요 차이점이 있다 ([4] 참조):

1. 우리는 relative position encoding을 사용한 global-local attention을 통해 구조화된 입력을 더 잘 처리할 수 있다.
2. Longformer와 달리, 우리는 CPC loss를 사용하여 global token을 학습하고, fine-tuning 과정에서 이들의 사용법을 학습한다.

E. 4 Classification

우리는 두 가지 유형의 분류 task를 시도한다. 문서 분류 (Document classification)
우리는 Table 15에 나열된 바와 같이, 다양한 길이와 내용을 가진 데이터셋에 대해 실험한다. 특히, 감성 분석(sentiment analysis) task (IMDb [64] 및 Yelp-5 [108])와 주제 할당(topic assignment) task (Arxiv [35], Patents [53], Hyperpartisan [47])를 살펴본다.

Table 14: 문서 분류를 위한 하이퍼파라미터.

Table 15: 분류 결과. 모든 데이터셋에 대해 F1 micro-averaged score를 보고한다. 더 작은 IMDb 및 Hyperpartisan 데이터셋에 대한 실험은 5회 반복되었으며, 평균 성능과 표준 편차가 함께 제시된다.

BERT를 따라, 우리는 BigBird encoder의 첫 번째 [CLS] 토큰 위에 cross entropy loss를 사용하는 단일 layer를 사용했으며, 이 encoder는 4096개의 토큰을 처리한다. 문서 분류 실험 결과는 Table 15에 보고되어 있다. 우리는 각 데이터셋에 대한 state-of-the-art (SoTA) 방법과 512 토큰으로 잘린(truncation) 일반 RoBERTa 모델과 비교한다. 모든 실험에서 우리는 처음 10% 스텝 동안 learning rate warmup을 사용했으며, learning rate의 선형 감소를 적용했다. 나머지 하이퍼파라미터의 상세 목록은 Table 14에 제공된다. 더 나은 정량적 평가를 위해, 우리는 **512 토큰을 초과하는 데이터셋의 비율(excess fraction)**을 계산했다. 이는 문서가 종종 잘리는(truncated) 길이이다. 우리는 문서 길이가 길고 학습 예시가 적을 때 BigBird 사용의 이점이 더 크다는 것을 확인했다. 예를 들어, 기본 크기 모델을 사용했을 때, BigBird는 Arxiv 데이터셋에서 state-of-the-art를 약 5% 포인트 향상시킨다. Patents 데이터셋에서는 단순 BERT/RoBERTa를 사용하는 것보다 향상이 있었지만, 대규모 학습 데이터 크기를 고려할 때 SoTA(BERT 기반이 아님) 대비 향상은 유의미하지 않았다. 이러한 성능 향상은 훨씬 작은 IMDb 데이터셋에서는 나타나지 않았다. 실험 설정 세부 사항과 함께, 우리는 경쟁력 있는 성능을 보여주는 상세 결과를 Appendix E.4에 제시한다.

Table 16: 기본 크기 모델에 대한 GLUE Dev 결과. 각 task 아래에 학습 예시 수가 보고된다. CoLA에 대해서는 MCC score, MRPC에 대해서는 F1 score, STS-B에 대해서는 Spearman correlation, 그리고 다른 task에 대해서는 accuracy score가 보고된다.

GLUE
General Language Understanding Evaluation (GLUE) 벤치마크 [92]는 8가지 다른 자연어 이해 task에 대해 언어 모델을 테스트한다. 우리는 https://github.com/pytorch/fairseq/blob/master/examples/roberta/README.glue.md에 언급된 것과 동일한 학습 파라미터를 사용했다. 우리 모델의 파라미터는 $b=64, g=2 \times b, w=3 \times b, r=3 \times b$이다 (우리는 MLM task로 사전학습된 BIGBIRD-ITC base 모델을 사용했다). Table 16에서 BigBird의 성능을 BERT, XLNet [101], RoBERTa와 비교한다. 우리는 훨씬 작은 context를 가진 task에서도 우리 모델의 성능이 full attention 모델과 경쟁력 있음을 확인했다.

E. 5 Summarization

Sec. 4.1에서 논의된 바와 같이, 출력 시퀀스의 길이가 짧기 때문에 우리는 encoder에만 sparse BigBIRD attention을 사용하고, decoder에는 full attention을 유지했다. encoder와 decoder의 hidden layer 수, head 수, hidden dimension은 동일하다. 하이퍼파라미터는 Tab. 17에 자세히 설명되어 있다. 우리의 결과는 Tab. 20에 요약되어 있다. 모든 실험에서 우리는 처음 10,000단계 동안 learning rate warmup을 사용했으며, 이후 learning rate는 제곱근 감쇠(square root decay) 방식을 적용했다.

Table 17: 요약(Summarization)을 위한 Encoder 하이퍼파라미터. Decoder에서는 full attention을 사용한다.

Table 18: 요약(Summarization)에 사용된 데이터셋 통계.

| | Instances | | | | Input Length | | | Output Length | | | :--- | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ---: | | Dataset | Training | Dev | Test | | Median | $90 \%$-ile | | Median | $90 \%$-ile | | BBC XSum [67] | 204044 | 11332 | 11334 | | 359 | 920 | | 25 | 32 | | CNN/DailyMail [36] | 287113 | 13368 | 11490 | | 777 | 1439 | | 59 | 93 |

Table 19: 더 짧은 요약 데이터셋 통계.

Table 20: 더 짧은 문서에 대한 요약 ROUGE 점수.

최근 여러 연구 [76, 63]의 성공에 따라, 우리는 encoder-decoder BIGBIRD Transformer 모델을 사전학습된 가중치로 warm start했으며, encoder와 decoder 간의 가중치를 공유했다. 특히, self-attention의 query/key/value matrix와 모든 feedforward layer는 encoder와 decoder 간에 공유된다. 무작위로 초기화되는 유일한 변수는 encoder-decoder attention이다.
Base 크기 모델의 경우, 우리는 App. E.1의 4096 시퀀스 길이에서 MLM으로 사전학습된 모델을 활용했으며, 이 모델은 다시 공개된 RoBERTa 체크포인트로 초기화되었다. Large 크기 모델의 경우, 요약 task를 위해 설계된 objective로 사전학습된 state-of-the-art Pegasus 모델 [107]의 가중치를 활용했다.
sparse attention이 full attention에 비해 상당한 성능 저하를 유발하는지 확인하기 위해, 우리는 문서 길이를 크게 자르지 않고도 full attention을 사용할 수 있는 두 개의 짧지만 인기 있는 데이터셋에 대해 추가 실험을 진행했다. 이 두 데이터셋의 통계는 Tab. 19에 있다. 우리는 우리의 성능이 경쟁력이 있음을 확인했으며, 이는 sparse attention이 full attention 모델과 유사한 성능을 달성할 수 있음을 보여준다.

F Genomics experiments details

이 섹션에서는 유전체학 데이터에 대한 BIGBIRD의 실험 설정에 대한 세부 정보를 제공한다.

F. 1 Pretraining

우리는 실험 설정을 일반적인 NLP 파이프라인과 최대한 유사하게 유지하고자 한다. 이를 위해, 우리는 인간 참조 유전체 GRCh37을 가져와 문서 $\mathcal{D}$로 변환한다. 각 문서 $d \in \mathcal{D}$는 문장들의 시퀀스이며, 각 문장은 DNA 단편들의 시퀀스이다. 우리는 문서를 다음과 같이 구성한다:

1. 빈 문서 집합 $D=\emptyset$으로 시작한다.
2. 각 염색체 $C$에 대해 다음 절차를 10회 반복한다. (a) 5' 말단에서 0에서 5000 염기쌍 사이의 시작점 $q$를 균일하게 무작위로 선택한다. (b) $q>|C|$가 될 때까지 반복한다. i. 문서당 문장 수를 나타내기 위해 50에서 100 사이의 숫자 $s$를 균일하게 무작위로 선택한다. ii. 연속적인 염기쌍(bps)을 사용하여 $s$개의 문장을 포함하는 문서 $d$를 구성한다. 각 문장의 길이는 500-1000 사이에서 균일하게 무작위로 선택된다. 따라서 결과 문서는 25,000-100,000 bps를 갖는다. iii. $D=D \bigcup d$ iv. $q=q+|d|$

이 절차를 통해 우리는 약 45만 개의 문서를 얻게 된다. 다음으로 우리는 결과 문서에 대해 sentencepiece [50] 토큰화를 실행한다. 특히, 5개의 문자를 구성 요소(염기 A, T, C, G에 대한 4개와 누락된 기호 N에 대한 1개)로 사용하여, 32k 크기의 byte pair encoding 테이블을 구성하며, 각 토큰은 평균 8.78 염기쌍을 나타낸다. 위에서 구성된 문서를 사용하여, Devlin et al. [22]에 따라 두 가지 사전학습(pretraining) task를 위한 데이터셋을 구성한다:

• Masked Language Model (MLM): 깊은 양방향 표현을 학습하기 위해 BERT 학습은 MLM task를 도입한다. 여기서 우리는 입력 토큰의 15%를 무작위로 마스킹하고, 이 마스킹된 토큰들을 예측한다. 이러한 마스킹된 토큰들을 단순히 [MASK] 플레이스홀더로 대체할 수 있지만, 이는 이러한 플레이스홀더가 없는 다운스트림 task에 대해 분포 불일치(distribution mis-match)를 초래한다. 이 문제를 완화하기 위해, 마스킹을 위해 선택된 15%의 토큰 중:
  • 80%의 토큰은 실제로 [MASK] 토큰으로 대체된다.
  • 10%의 토큰은 무작위 토큰으로 대체된다.
  • 10%의 토큰은 변경되지 않은 채로 남지만, 출력에서 여전히 예측된다.

우리는 이 전체 시퀀스를 BIGBIRD Transformer encoder를 통해 실행한 다음, 시퀀스 내의 다른 마스킹되지 않은 토큰들이 제공하는 컨텍스트를 기반으로 마스킹된 위치에 해당하는 토큰을 예측한다.

• Next Sentence Prediction (NSP): 두 시퀀스 간의 관계를 이해하기 위해 BERT 학습은 NSP task를 도입한다. 여기서 우리는 주어진 시퀀스 쌍이 연속적인지 아닌지를 예측한다. 학습 중에 모델은 [SEP] 토큰으로 구분된 시퀀스 쌍과 시작 부분에 [CLS] 토큰을 입력으로 받는다. 전체 입력 패턴은 [CLS] sequence A [SEP] sequence B [SEP]이다. 50%의 경우 두 번째 시퀀스는 첫 번째 시퀀스 다음의 실제 시퀀스에서 가져온다. 나머지 50%의 경우 전체 데이터셋에서 무작위 시퀀스를 가져온다. 모델은 [CLS] 토큰에 해당하는 출력을 사용하여 이 관계를 예측해야 하며, 이 출력은 간단한 이진 분류 레이어에 공급된다. https://www.ncbi.nlm.nih.gov/assembly/GCF_000001405.39

Figure 7: 원본 DNA 데이터셋에서 masked language modeling 데이터가 어떻게 생성되었는지에 대한 시각적 설명. GRCh37의 원본 DNA 시퀀스는 무작위 위치에서 분할되어 50-100개의 문장을 가진 문서를 생성했으며, 각 문장은 500-1000 염기쌍(bps)이었다. 따라서 각 문서는 25000-100,000 bps의 연속적인 DNA 가닥을 가졌다. 이 과정은 GRCH37의 각 염색체에 대해 10세트의 문서를 생성하기 위해 10회 반복되었다. 결과 문서 세트는 Sentencepiece를 통과하여 평균 8bp의 토큰을 생성했다. 사전학습을 위해 우리는 masked language model을 사용하고 토큰의 10%를 마스킹한 다음 마스킹된 토큰을 예측하도록 학습했다.

단계 시퀀스는 Fig. 9에 시각적으로 자세히 설명되어 있다. 모델은 MLM과 NSP를 함께 학습한다. 학습 하이퍼파라미터는 Tab. 21의 두 번째 열에 제공된다. 모든 실험에서 우리는 처음 10,000단계 동안 learning rate warmup을 사용하고, learning rate의 선형 감소를 사용한다. 우리는 또한 NLP와 유사하게 더 큰 컨텍스트를 갖는 것이 성능을 향상시킨다는 가설을 검증하기 위해 간단한 ablation study를 수행했다. 우리는 BigBird가 다른 길이의 시퀀스에서 어떻게 수행되는지 테스트하기 위해 위에서 설명한 MLM task를 사용했다. 시퀀스 길이가 증가함에 따른 MLM task의 정확도는 Fig. 8에 나와 있다. 더 긴 컨텍스트는 최종 정확도를 향상시킬 뿐만 아니라 더 빠른 학습을 가능하게 한다.

Figure 8: 컨텍스트 길이에 따른 BigBird 정확도.

F. 2 Promoter Region Prediction

프로모터(promoter) 영역은 전사 개시(transcription initiation)에 중요한 역할을 하므로, 이를 인식하는 것은 생물정보학 분야에서 중요한 관심 영역이다. Oubounyt et al. [71]의 연구를 따라, 우리는 Eukaryotic Promoter Database (EPDnew) [24] 에서 제공하는 데이터셋을 사용하며, 이 데이터셋은 인간 게놈 내 29,597개의 프로모터 영역을 포함한다. 전사 개시점(TSS)을 중심으로, 우리는 인간 참조 게놈 GRCh37에서 8000 bp (-5000 ~ +3000 bp) 길이의 시퀀스를 추출한다. EPDnew는 최신 GRCh38을 사용하므로, 우리는 LiftOver [44] 를 사용하여 GRCh37 좌표로 변환한다.

Figure 9: GRCh37의 원시 DNA 시퀀스 중 주어진 비코딩 영역에 대한 크로마틴 프로파일을 예측하는 DNA 세그먼트의 시각적 설명. 우리는 주어진 비코딩 영역 전후로 8000 bp의 DNA를 context로 사용한다. 양쪽에 context를 포함한 완전한 DNA 단편은 토큰화되어 입력 시퀀스를 형성한다. 이 task는 160개의 다른 전사 인자(TF)에 대한 690개의 TF 결합 프로파일, 125개의 DNase I 민감도(DHS) 프로파일, 104개의 히스톤 마크(HM) 프로파일을 포함한 총 919개의 크로마틴 프로파일을 예측하는 것이다.

Oubounyt et al. [71]의 방식을 따라, 각 프로모터 영역 예시(양성 예시)에 대해 동일한 크기의 음성 예시(비프로모터 시퀀스)를 다음과 같이 구성한다: 양성 시퀀스를 20개의 하위 시퀀스로 나눈다. 그런 다음, 12개의 하위 시퀀스를 무작위로 선택하여 무작위로 대체한다. 나머지 8개의 하위 시퀀스는 보존된다. 이 과정은 [71]의 Figure 1에 설명되어 있다. 이 과정을 양성 세트에 적용하면, 프로모터 시퀀스에서 보존된 부분(변경되지 않은 하위 시퀀스, 20개 중 8개)을 포함하는 새로운 비프로모터 시퀀스가 생성된다. 이러한 파라미터는 시퀀스의 32%에서 40%가 프로모터 시퀀스의 보존된 부분을 포함하는 음성 세트를 생성할 수 있게 한다.

각 예시의 앞과 뒤에 각각 [CLS] 및 [SEP] 토큰을 추가한다. BIGBIRD Transformer encoder에서 [CLS] 토큰에 해당하는 출력은 간단한 이진 분류 레이어에 입력된다. 우리는 App. F.1의 사전학습된 BigBird를 Tab. 21에 설명된 하이퍼파라미터를 사용하여 fine-tuning한다. 음성 예시 생성 방식과 MLM pretraining의 본질적인 유사성으로 인해 높은 성능은 놀라운 일이 아니다.

F. 3 Chromatin-Profile Prediction

non-coding 효과를 예측하기 위한 시퀀스 기반 알고리즘 프레임워크의 첫 번째 단계는 대규모 chromatic profile을 예측하는 모델을 구축하는 것이다 [109]. 본 논문에서는 Zhou와 Troyanskaya [109]가 제공한 데이터셋을 사용하여 BIGBIRD를 학습시켜 chromatic profile을 예측한다.

Table 21: Computational biology를 위한 하이퍼파라미터 표.

각 학습 샘플은 인간 GRCh37 참조 유전체에서 각 200-bp bin을 중심으로 하는 8,000-bp 시퀀스로 구성되며, 919개의 chromatin feature에 대한 레이블 벡터와 짝을 이룬다. 이전과 마찬가지로, 각 예시의 앞과 뒤에 각각 [CLS] 및 [SEP] token을 추가한다. BIGBIRD Transformer encoder에서 [CLS] token에 해당하는 출력은 919개의 head를 가진 linear layer에 입력된다. 따라서 우리는 919개의 독립적인 이진 분류 문제를 동시에 예측한다. 우리는 App. F.1의 사전학습된 BigBird를 Tab. 21에 설명된 하이퍼파라미터를 사용하여 fine-tuning한다. 데이터가 **매우 불균형(양성 예시보다 음성 예시가 훨씬 많음)**하기 때문에, 양성 예시에 대한 loss function에 8배의 가중치를 부여했다.

우리는 Zhou와 Troyanskaya [109]가 제공한 학습 및 테스트 분할을 사용했으며, 이는 염색체를 기반으로 엄격하게 겹치지 않도록 구성되었다. 염색체 8번과 9번은 chromatin feature 예측 성능 테스트를 위해 학습에서 제외되었고, 나머지 상염색체는 학습 및 검증에 사용되었다. 염색체 7번의 30,508,751-35,296,850 유전체 좌표에 걸쳐 있는 4,000개의 샘플이 검증 세트로 사용되었다.

DeepSea Zhou와 Troyanskaya [109]에서 각 시퀀스에 대한 예측 확률이 정방향 및 상보적 시퀀스 쌍에 대한 확률 예측의 앙상블 평균으로 계산되었기 때문에, 우리도 독립적으로 학습된 두 개의 BIGBIRD 모델 앙상블을 사용하여 예측한다.