Mathematics for Machine Learning-Chapter6

Deisenroth, Marc Peter, A. Aldo Faisal, and Cheng Soon Ong. Mathematics for machine learning. Cambridge University Press, 2020.

6

확률 변수 확률 분포

Probability and Distributions

확률은 느슨하게 말해 **불확실성(uncertainty)**에 대한 연구와 관련이 있다. 확률은 어떤 사건이 발생하는 횟수의 비율로 생각할 수도 있고, 사건에 대한 믿음의 정도로 생각할 수도 있다. 우리는 이 확률을 사용하여 실험에서 어떤 일이 발생할 가능성을 측정하고자 한다. 1장에서 언급했듯이, 우리는 종종 데이터의 불확실성, 머신러닝 모델의 불확실성, 그리고 모델이 생성하는 예측의 불확실성을 정량화한다. 불확실성을 정량화하려면 **확률 변수(random variable)**의 개념이 필요하다. 확률 변수는 무작위 실험의 결과를 우리가 관심 있는 속성 집합으로 매핑하는 함수이다. 확률 변수와 관련하여 특정 결과(또는 결과 집합)가 발생할 확률을 측정하는 함수가 있는데, 이를 **확률 분포(probability distribution)**라고 한다.

확률 분포는 확률 모델링(probabilistic modeling)(섹션 8.4), 그래픽 모델(graphical models)(섹션 8.5), 모델 선택(model selection)(섹션 8.6)과 같은 다른 개념들의 구성 요소로 사용된다. 다음 섹션에서는 확률 공간을 정의하는 세 가지 개념(표본 공간, 사건, 사건의 확률)과 이들이 확률 변수라는 네 번째 개념과 어떻게 관련되는지를 제시한다. 엄격한 설명은 개념 뒤에 숨겨진 직관을 가릴 수 있으므로, 설명은 의도적으로 다소 비형식적이다. 이 장에서 제시된 개념들의 개요는 Figure 6.1에 나와 있다.

6.1 Construction of a Probability Space

확률 이론은 실험의 무작위 결과를 설명하기 위한 수학적 구조를 정의하는 것을 목표로 한다. 예를 들어, 동전 하나를 던질 때 그 결과를 예측할 수는 없지만, 많은 수의 동전 던지기를 통해 평균 결과에서 규칙성을 관찰할 수 있다. 이러한 확률의 수학적 구조를 사용하여 자동화된 추론을 수행하는 것이 목표이며, 이러한 의미에서 확률은 논리적 추론을 일반화한다 (Jaynes, 2003).

6.1.1 Philosophical Issues

자동화된 추론 시스템을 구축할 때, 고전적인 Boolean logic으로는 특정 형태의 **그럴듯한 추론(plausible reasoning)**을 표현할 수 없다. 다음 시나리오를 고려해 보자:

이 자료는 Marc Peter Deisenroth, A. Aldo Faisal, Cheng Soon Ong이 저술한 Mathematics for Machine Learning (2020)으로 Cambridge University Press에서 출판되었다. 이 버전은 개인적인 용도로만 무료로 열람 및 다운로드할 수 있다. 재배포, 재판매 또는 파생 저작물에 사용할 수 없다. ©by M. P. Deisenroth, A. A. Faisal, and C. S. Ong, 2021. https://mml-book.com.

그림 6.1 본 장에서 설명하는 random variable 및 probability distribution 관련 개념들의 마인드맵.

우리는 $A$가 거짓임을 관찰한다. 그러면 $B$가 덜 그럴듯해진다고 생각하지만, 고전 논리로는 어떤 결론도 내릴 수 없다. $B$가 참임을 관찰하면 $A$가 더 그럴듯해지는 것처럼 보인다. 우리는 이러한 형태의 추론을 매일 사용한다. 친구를 기다리면서 세 가지 가능성을 고려한다: H1, 친구가 제시간에 온다; H2, 친구가 교통 체증으로 지연되었다; H3, 친구가 외계인에게 납치되었다. 친구가 늦는 것을 관찰하면 논리적으로 H1을 배제해야 한다. 또한 H2가 더 가능성이 높다고 생각하는 경향이 있지만, 논리적으로 그렇게 해야 할 필요는 없다. 마지막으로 H3도 가능하다고 생각할 수 있지만, 여전히 매우 가능성이 낮다고 간주한다. 어떻게 H2가 가장 그럴듯한 답이라고 결론 내릴 수 있을까? 이러한 관점에서 **확률론(probability theory)**은 Boolean logic의 일반화로 간주될 수 있다. 머신러닝의 맥락에서는 자동화된 추론 시스템 설계를 공식화하기 위해 종종 이러한 방식으로 적용된다. 확률론이 추론 시스템의 기초가 되는 방법에 대한 추가 논의는 Pearl (1988)에서 찾을 수 있다.

확률의 철학적 기반과 그것이 우리가 참이라고 생각해야 하는 것(논리적 의미에서)과 어떻게든 관련되어야 하는지에 대한 연구는 Cox에 의해 이루어졌다 (Jaynes, 2003). "그럴듯한 추론을 위해서는 진리의 이산적인 참/거짓 값을 연속적인 그럴듯함으로 확장해야 한다" (Jaynes, 2003). 또 다른 생각은 우리의 상식에 대해 정확하게 접근하면 결국 확률을 구성하게 된다는 것이다. E. T. Jaynes (1922-1998)는 모든 그럴듯함에 적용되어야 하는 세 가지 수학적 기준을 제시했다:

1. **그럴듯함의 정도(degrees of plausibility)**는 **실수(real numbers)**로 표현된다.
2. 이 숫자들은 **상식의 규칙(rules of common sense)**에 기반해야 한다.
3. 결과적인 추론은 "일관성(consistent)"이라는 단어의 다음 세 가지 의미와 함께 일관성을 가져야 한다: (a) 일관성 또는 비모순성(Consistency or non-contradiction): 동일한 결과가 다른 수단을 통해 도출될 수 있을 때, 모든 경우에 동일한 그럴듯함 값이 발견되어야 한다. (b) 정직성(Honesty): 사용 가능한 모든 데이터가 고려되어야 한다. (c) 재현성(Reproducibility): 두 문제에 대한 우리의 지식 상태가 동일하다면, 우리는 두 문제에 동일한 그럴듯함의 정도를 할당해야 한다.

Cox-Jaynes 정리는 이러한 그럴듯함이 임의의 **단조 함수(monotonic function)**에 의한 변환까지, 그럴듯함 $p$에 적용되는 보편적인 수학적 규칙을 정의하기에 충분하다는 것을 증명한다. 결정적으로, 이러한 규칙들은 확률의 규칙이다. 참고. 머신러닝 및 통계학에는 확률에 대한 두 가지 주요 해석이 있다: 베이즈(Bayesian) 해석과 빈도주의(frequentist) 해석 (Bishop, 2006; Efron and Hastie, 2016). 베이즈 해석은 사용자가 어떤 사건에 대해 가지고 있는 불확실성의 정도를 명시하기 위해 확률을 사용한다. 때로는 "주관적 확률(subjective probability)" 또는 "믿음의 정도(degree of belief)"라고도 불린다. 빈도주의 해석은 관심 있는 사건의 상대적 빈도를 발생한 총 사건 수에 대해 고려한다. 사건의 확률은 무한한 데이터가 있을 때 극한에서 사건의 상대적 빈도로 정의된다.

확률 모델에 대한 일부 머신러닝 텍스트는 혼란스러운 게으른 표기법과 전문 용어를 사용한다. 이 텍스트도 예외는 아니다. 여러 개의 서로 다른 개념들이 모두 "probability distribution"으로 지칭되며, 독자는 종종 맥락에서 의미를 파악해야 한다. probability distribution을 이해하는 데 도움이 되는 한 가지 요령은 우리가 **범주형(categorical) 모델(이산 random variable)**을 모델링하려는 것인지 **연속형(continuous) 모델(연속 random variable)**을 모델링하려는 것인지 확인하는 것이다. 머신러닝에서 다루는 질문의 종류는 우리가 범주형 모델을 고려하는지 연속형 모델을 고려하는지와 밀접하게 관련되어 있다.

6.1.2 Probability and Random Variables

확률을 논할 때 종종 혼동되는 세 가지 아이디어가 있다. 첫 번째는 **확률 공간(probability space)**이라는 개념으로, 이를 통해 확률의 아이디어를 정량화할 수 있다. 그러나 우리는 대부분 이 기본적인 확률 공간을 직접 다루지 않는다. 대신, 확률을 더 편리한 (종종 수치적인) 공간으로 옮기는 확률 변수(random variables)(두 번째 아이디어)를 사용한다. 세 번째 아이디어는 확률 변수와 관련된 **분포(distribution) 또는 법칙(law)**의 개념이다. 이 섹션에서는 처음 두 가지 아이디어를 소개하고, 세 번째 아이디어는 섹션 6.2에서 자세히 다룰 것이다.

현대 확률론은 Kolmogorov가 제안한 일련의 공리(Grinstead and Snell, 1997; Jaynes, 2003)에 기반을 두고 있으며, 이는 표본 공간(sample space), 사건 공간(event space), **확률 측도(probability measure)**의 세 가지 개념을 도입한다. 확률 공간은 무작위 결과(random outcomes)를 가진 실제 세계의 과정(실험이라고 함)을 모델링한다.

The sample space $\Omega$

**표본 공간(sample space)**은 실험에서 발생할 수 있는 모든 가능한 결과들의 집합이며, 일반적으로 $\Omega$로 표기한다. 예를 들어, 두 번 연속으로 동전을 던지는 실험의 표본 공간은 $\{h h, t t, h t, t h\}$이며, 여기서 "h"는 "앞면(heads)"을, "t"는 "뒷면(tails)"을 나타낸다.

The event space $\mathcal{A}$

**사건 공간(event space)**은 실험의 잠재적 결과들의 공간이다. 표본 공간 $\Omega$의 부분집합 $A$가 사건 공간 $\mathcal{A}$에 속한다는 것은, 실험이 끝났을 때 특정 결과 $\omega \in \Omega$가 $A$에 속하는지 여부를 관찰할 수 있다는 의미이다. 사건 공간 $\mathcal{A}$는 $\Omega$의 부분집합들의 집합을 고려하여 얻어지며, 이산 확률 분포(섹션 6.2.1)의 경우 $\mathcal{A}$는 종종 $\Omega$의 **멱집합(power set)**이다.

The probability $P$

각 이벤트 $A \in \mathcal{A}$에 대해, 우리는 이벤트가 발생할 확률 또는 믿음의 정도를 측정하는 숫자 $P(A)$를 연관시킨다. $P(A)$는 $A$의 확률이라고 불린다.

단일 이벤트의 확률은 구간 $[0,1]$ 안에 있어야 하며, 표본 공간 $\Omega$의 모든 결과에 대한 총 확률은 1이어야 한다. 즉, $P(\Omega)=1$이다. 확률 공간 $(\Omega, \mathcal{A}, P)$이 주어졌을 때, 우리는 이를 사용하여 어떤 실제 현상을 모델링하고자 한다. 머신러닝에서는 종종 확률 공간을 명시적으로 언급하는 것을 피하고, 대신 우리가 $\mathcal{T}$로 나타내는 관심 있는 양에 대한 확률을 언급한다. 이 책에서 우리는 $\mathcal{T}$를 **타겟 공간(target space)**이라고 부르며, $\mathcal{T}$의 원소를 **상태(states)**라고 부른다. 우리는 $\Omega$의 원소(결과)를 취하여 $\mathcal{T}$의 값인 특정 관심 양 $x$를 반환하는 함수 $X: \Omega \rightarrow \mathcal{T}$를 도입한다. $\Omega$에서 $\mathcal{T}$로의 이러한 연관/매핑을 **확률 변수(random variable)**라고 한다. 예를 들어, 두 개의 동전을 던지고 앞면의 수를 세는 경우, 확률 변수 $X$는 세 가지 가능한 결과에 매핑된다: $X(\mathrm{hh})=2, X(\mathrm{ht})=1, X(\mathrm{th})=1, X(\mathrm{tt})=0$. 이 특정 경우에 $\mathcal{T}=\{0,1,2\}$이며, 우리가 관심 있는 것은 $\mathcal{T}$의 원소에 대한 확률이다. 유한 표본 공간 $\Omega$와 유한 $\mathcal{T}$에 대해, 확률 변수에 해당하는 함수는 본질적으로 **룩업 테이블(lookup table)**이다. $\mathcal{T}$의 모든 부분집합 $S \subseteq \mathcal{T}$에 대해, 우리는 확률 변수 $X$에 해당하는 특정 이벤트 발생에 $P_{X}(S) \in[0,1]$ (확률)을 연관시킨다. 예제 6.1은 이 용어에 대한 구체적인 설명을 제공한다. 참고. 앞서 언급된 표본 공간 $\Omega$는 불행히도 책마다 다른 이름으로 불린다. $\Omega$의 또 다른 일반적인 이름은 "상태 공간(state space)"(Jacod and Protter, 2004)이지만, 상태 공간은 때때로 동적 시스템의 상태를 지칭하는 데 사용되기도 한다(Hasselblatt and 표본 공간 이벤트 공간 확률 타겟 공간 확률 변수

"확률 변수"라는 이름은 무작위적이지도 않고 변수도 아니기 때문에 큰 오해의 원인이 된다. 그것은 함수이다.

이 장난감 예시는 본질적으로 편향된 동전 던지기 예시이다.

Katok, 2003). $\Omega$를 설명하는 데 때때로 사용되는 다른 이름은 "표본 기술 공간(sample description space)", "가능성 공간(possibility space)", "이벤트 공간(event space)"이다.

Example 6.1

독자는 사건 집합의 교집합과 합집합의 확률 계산에 이미 익숙하다고 가정한다. 확률에 대한 더 쉬운 소개와 많은 예시는 Walpole et al. (2011)의 2장에서 찾을 수 있다.

주머니에서 두 개의 동전을 뽑는(교체 포함) 유원지 게임을 모델링하는 통계적 실험을 고려해 보자. 주머니에는 미국 동전(\$$로 표시)과 영국 동전(£$로 표시)이 있으며, 주머니에서 두 개의 동전을 뽑으므로 총 네 가지 결과가 있다. 이 실험의 **상태 공간(state space)** 또는 **표본 공간(sample space)**$\Omega$는$($, $)$,$($, £)$,$(£, $)$,$(£, £)$이다. 동전 주머니의 구성이 무작위로$$$를 뽑을 확률이 0.3이라고 가정해 보자.

우리가 관심 있는 사건은 반복된 뽑기에서 \$$가 나오는 총 횟수이다. 표본 공간 \Omega$를$\mathcal{T}$로 매핑하는 **확률 변수(random variable)**$X$를 정의해 보자. 여기서$\mathcal{T}$는 주머니에서$$$를 뽑는 횟수를 나타낸다. 앞선 표본 공간에서$$$가 0개, 1개 또는 2개 나올 수 있음을 알 수 있으며, 따라서$\mathcal{T}={0,1,2}$이다. 확률 변수$X$(함수 또는 조회 테이블)는 다음과 같은 테이블로 나타낼 수 있다:

$$\begin{array}{r} X((\$, \$))=2 \\ X((\$, £))=1 \\ X((£, \$))=1 \\ X((£, £))=0 . \end{array}$$

두 번째 동전을 뽑기 전에 첫 번째 뽑은 동전을 다시 넣으므로, 이는 두 번의 뽑기가 서로 **독립적(independent)**임을 의미한다. 이에 대해서는 섹션 6.4.5에서 논의할 것이다. 두 번의 뽑기 중 한 번만 \$$가 나오는 동일한 사건에 매핑되는 두 가지 실험 결과가 있음에 유의하라. 따라서 X$의 확률 질량 함수(probability mass function)(섹션 6.2.1)는 다음과 같이 주어진다:

$$\begin{aligned} P(X=2) & =P((\$, \$)) \\ & =P(\$) \cdot P(\$) \\ & =0.3 \cdot 0.3=0.09 \\ P(X=1) & =P((\$, £) \cup(£, \$)) \\ & =P((\$, £))+P((£, \$)) \\ & =0.3 \cdot(1-0.3)+(1-0.3) \cdot 0.3=0.42 \\ P(X=0) & =P((£, £)) \\ & =P(£) \cdot P(£) \\ & =(1-0.3) \cdot(1-0.3)=0.49 \end{aligned}$$

계산에서 우리는 $X$의 출력 확률과 $\Omega$의 표본 확률이라는 두 가지 다른 개념을 동일시했다. 예를 들어, (6.7)에서 우리는 $P(X=0)=P((£, £))$라고 말한다. 확률 변수 $X: \Omega \rightarrow \mathcal{T}$와 $\mathcal{T}$의 부분 집합 $S \subseteq \mathcal{T}$를 고려해 보자(예를 들어, 두 개의 동전을 던졌을 때 한 개의 앞면이 나오는 결과와 같은 $\mathcal{T}$의 단일 요소). $X^{-1}(S)$를 $X$에 의한 $S$의 **원상(pre-image)**이라고 하자. 즉, $X$에 따라 $S$로 매핑되는 $\Omega$의 요소 집합이다; $\{\omega \in \Omega: X(\omega) \in S\}$. 확률 변수 $X$를 통해 $\Omega$의 사건에서 확률이 변환되는 방식을 이해하는 한 가지 방법은 이를 $S$의 원상 확률과 연관시키는 것이다 (Jacod and Protter, 2004). $S \subseteq \mathcal{T}$에 대해 우리는 다음 표기법을 사용한다:

$$P_{X}(S)=P(X \in S)=P\left(X^{-1}(S)\right)=P(\{\omega \in \Omega: X(\omega) \in S\})$$

(6.8)의 좌변은 우리가 관심 있는 가능한 결과 집합의 확률(예: \$$의 개수 = 1)이다. 상태를 결과로 매핑하는 확률 변수 X$를 통해 (6.8)의 우변에서 이것이 특정 속성(예:$$ £, £ $ $)을 갖는 상태 집합($\Omega$내)의 확률임을 알 수 있다. 우리는 확률 변수$X$가 특정 확률 분포$P_{X}$에 따라 분포된다고 말한다. 이 분포는 사건과 확률 변수의 결과 확률 사이의 확률 매핑을 정의한다. 다시 말해, 함수$P_{X}$또는 동등하게$P \circ X^{-1}$는 확률 변수$X$의 **법칙(law)** 또는 **분포(distribution)**이다. 참고. **목표 공간(target space)**, 즉 확률 변수$X$의 **범위(range)**$\mathcal{T}$는 확률 공간의 종류, 즉$\mathcal{T}$확률 변수를 나타내는 데 사용된다.$\mathcal{T}$가 유한하거나 가산 무한할 때, 이를 **이산 확률 변수(discrete random variable)**(섹션 6.2.1)라고 한다. **연속 확률 변수(continuous random variables)**(섹션 6.2.2)의 경우, 우리는$\mathcal{T}=\mathbb{R}$또는$\mathcal{T}=\mathbb{R}^{D}$만 고려한다.

6.1.3 Statistics

확률론과 통계학은 종종 함께 제시되지만, 불확실성의 다른 측면을 다룬다. 이 둘을 대조하는 한 가지 방법은 고려되는 문제의 종류에 따른 것이다. 확률론을 사용하면, 우리는 어떤 프로세스의 모델을 고려할 수 있는데, 여기서 기저의 불확실성은 확률 변수에 의해 포착되며, 우리는 확률 규칙을 사용하여 어떤 일이 발생하는지 도출한다. 통계학에서는 어떤 일이 발생한 것을 관찰하고, 그 관찰을 설명하는 기저의 프로세스를 파악하려고 노력한다. 이러한 의미에서 머신러닝은 데이터를 생성한 프로세스를 적절하게 나타내는 모델을 구축하려는 목표에서 통계학과 가깝다. 우리는 확률 규칙을 사용하여 일부 데이터에 대한 "가장 적합한" 모델을 얻을 수 있다.

머신러닝 시스템의 또 다른 측면은 우리가 **일반화 오차(generalization error)**에 관심이 있다는 것이다(8장 참조). 이는 우리가 지금까지 본 인스턴스와 동일하지 않은, 미래에 관찰할 인스턴스에 대한 시스템의 성능에 실제로 관심이 있다는 것을 의미한다. 미래 성능에 대한 이러한 분석은 확률과 통계에 의존하며, 대부분은 이 장에서 제시될 내용을 넘어선다. 관심 있는 독자는 Boucheron et al. (2013)과 Shalev-Shwartz and Ben-David (2014)의 책을 참고하는 것이 좋다. 통계에 대해서는 8장에서 더 자세히 다룰 것이다.

6.2 Discrete and Continuous Probabilities

섹션 6.1에서 소개된 사건의 확률을 설명하는 방법에 초점을 맞춰보자. target space가 이산적인지 연속적인지에 따라 분포를 지칭하는 자연스러운 방식이 다르다. target space $\mathcal{T}$가 이산적일 때, 우리는 확률 변수 $X$가 특정 값 $x \in \mathcal{T}$를 취할 확률을 $P(X=x)$로 나타낼 수 있다. 이산 확률 변수 $X$에 대한 표현 $P(X=x)$는 **확률 질량 함수(probability mass function)**라고 알려져 있다. target space $\mathcal{T}$가 연속적일 때, 예를 들어 실수선 $\mathbb{R}$과 같은 경우, 확률 변수 $X$가 구간에 속할 확률을 $P(a \leqslant X \leqslant b)$ (단, $a<b$)로 지정하는 것이 더 자연스럽다. 관례적으로 우리는 확률 변수 $X$가 특정 값 $x$보다 작을 확률을 $P(X \leqslant x)$로 지정한다. 연속 확률 변수 $X$에 대한 표현 $P(X \leqslant x)$는 **누적 분포 함수(cumulative distribution function)**라고 알려져 있다. 우리는 섹션 6.2.2에서 연속 확률 변수에 대해 논의할 것이다. 섹션 6.2.3에서 명명법을 다시 살펴보고 이산 확률 변수와 연속 확률 변수를 대조할 것이다.

참고. 우리는 단일 확률 변수(상태는 비볼드체 $x$로 표시됨)의 분포를 지칭하기 위해 **단변량 분포(univariate distribution)**라는 용어를 사용할 것이다. 둘 이상의 확률 변수 분포는 **다변량 분포(multivariate distributions)**라고 부를 것이며, 일반적으로 확률 변수 벡터(상태는 볼드체 $\boldsymbol{x}$로 표시됨)를 고려할 것이다.

6.2.1 Discrete Probabilities

타겟 공간이 이산적일 때, 우리는 여러 확률 변수의 확률 분포가 (다차원) 숫자 배열을 채우는 것으로 상상할 수 있다. 그림 6.2는 그 예시를 보여준다. 결합 확률의 타겟 공간은 각 확률 변수의 타겟 공간의 **카르테시안 곱(Cartesian product)**이다. 우리는 결합 확률을 두 값의 결합된 항목으로 정의한다.

$$P\left(X=x_{i}, Y=y_{j}\right)=\frac{n_{i j}}{N},$$

여기서 $n_{i j}$는 상태 $x_{i}$와 $y_{j}$를 갖는 이벤트의 수이고, $N$은 총 이벤트의 수이다. 결합 확률은 두 이벤트의 교집합 확률, 즉 $P\left(X=x_{i}, Y=y_{j}\right)=P\left(X=x_{i} \cap Y=y_{j}\right)$이다. 그림 6.2는 이산 확률 분포의 **확률 질량 함수(probability mass function, pmf)**를 보여준다. 두 확률 변수 $X$와 $Y$에 대해, $X=x$이고 $Y=y$일 확률은 (간략하게) $p(x, y)$로 쓰이며 **결합 확률(joint probability)**이라고 불린다. 확률은 상태 $x$와 $y$를 취하여 실수 값을 반환하는 함수로 생각할 수 있으며, 이것이 우리가 $p(x, y)$라고 쓰는 이유이다. 확률 변수 $Y$의 값에 관계없이 $X$가 $x$ 값을 취할 **주변 확률(marginal probability)**은 (간략하게) $p(x)$로 쓰인다. 우리는 확률 변수 $X$가 $p(x)$에 따라 분포됨을 나타내기 위해 $X \sim p(x)$라고 쓴다. 만약 우리가 $X=x$인 경우만 고려한다면, $Y=y$인 경우의 비율(조건부 확률)은 (간략하게) $p(y \mid x)$로 쓰인다.

Example 6.2

그림 6.2에 나타난 바와 같이, $X$는 다섯 가지 가능한 상태를 가지고 $Y$는 세 가지 가능한 상태를 가지는 두 개의 확률 변수 $X$와 $Y$를 고려해 보자. 우리는 상태 $X=x_{i}$와 $Y=y_{j}$를 갖는 사건의 수를 $n_{i j}$로 나타내고, 총 사건의 수를 $N$으로 나타낸다. 값 $c_{i}$는 $i$번째 열에 대한 개별 빈도의 합, 즉 $c_{i}=\sum_{j=1}^{3} n_{i j}$이다. 유사하게, 값 $r_{j}$는 행의 합, 즉 $r_{j}=\sum_{i=1}^{5} n_{i j}$이다. 이러한 정의를 사용하여 $X$와 $Y$의 분포를 간결하게 표현할 수 있다.

각 확률 변수의 확률 분포인 **주변 확률(marginal probability)**은 행 또는 열의 합으로 볼 수 있다.

$$P\left(X=x_{i}\right)=\frac{c_{i}}{N}=\frac{\sum_{j=1}^{3} n_{i j}}{N}$$

그리고

$$P\left(Y=y_{j}\right)=\frac{r_{j}}{N}=\frac{\sum_{i=1}^{5} n_{i j}}{N}$$

여기서 $c_{i}$와 $r_{j}$는 각각 확률 테이블의 $i$번째 열과 $j$번째 행이다. 관례적으로, 유한한 수의 사건을 갖는 이산 확률 변수의 경우, 확률의 합은 1이 된다고 가정한다. 즉,

$$\sum_{i=1}^{5} P\left(X=x_{i}\right)=1 \quad \text { and } \quad \sum_{j=1}^{3} P\left(Y=y_{j}\right)=1 .$$

**조건부 확률(conditional probability)**은 특정 행 또는 열의 비율이다.

Figure 6.2

확률 변수 $X$와 $Y$를 갖는 이산 이변량 확률 질량 함수의 시각화. 이 다이어그램은 Bishop (2006)에서 발췌했다. 주변 확률 조건부 확률 특정 셀. 예를 들어, $X$가 주어졌을 때 $Y$의 조건부 확률은 다음과 같다.

$$P\left(Y=y_{j} \mid X=x_{i}\right)=\frac{n_{i j}}{c_{i}}$$

그리고 $Y$가 주어졌을 때 $X$의 조건부 확률은 다음과 같다.

$$P\left(X=x_{i} \mid Y=y_{j}\right)=\frac{n_{i j}}{r_{j}}$$

머신러닝에서 우리는 이산 확률 분포를 사용하여 범주형 변수(categorical variables), 즉 유한한 비순서 값 집합을 취하는 변수를 모델링한다. 이들은 사람의 급여를 예측하는 데 사용되는 대학 학위와 같은 범주형 특징(categorical features)이거나, 필기 인식을 할 때 알파벳 글자와 같은 범주형 레이블(categorical labels)일 수 있다. 이산 분포는 또한 유한한 수의 연속 분포를 결합하는 확률 모델을 구성하는 데 자주 사용된다 (11장).

6.2.2 Continuous Probabilities

이 섹션에서는 **실수 값 확률 변수(real-valued random variables)**를 고려한다. 즉, 실수선 $\mathbb{R}$의 구간인 목표 공간(target spaces)을 고려한다. 이 책에서는 유한 상태를 가진 이산 확률 공간(discrete probability spaces)이 있는 것처럼 실수 확률 변수에 대한 연산을 수행할 수 있다고 가정한다. 그러나 이러한 단순화는 두 가지 상황에서 정확하지 않다: 무언가를 무한히 반복할 때와 구간에서 한 점을 추출하고자 할 때이다. 첫 번째 상황은 머신러닝에서 **일반화 오차(generalization errors)**를 논의할 때 발생한다(8장). 두 번째 상황은 **가우시안(Gaussian)**과 같은 **연속 분포(continuous distributions)**를 논의하고자 할 때 발생한다(섹션 6.5). 우리의 목적상, 이러한 부정확성은 확률에 대한 더 간략한 소개를 가능하게 한다.

참고. 연속 공간에는 두 가지 추가적인 기술적 문제점이 있는데, 이는 직관에 반한다. 첫째, 모든 부분집합의 집합(섹션 6.1에서 사건 공간(event space) $\mathcal{A}$를 정의하는 데 사용됨)은 충분히 잘 동작하지 않는다. $\mathcal{A}$는 집합 보수(set complements), 집합 교집합(set intersections), 집합 합집합(set unions)에 대해 잘 동작하도록 제한되어야 한다. 둘째, 집합의 크기(이산 공간에서는 원소를 세어 얻을 수 있음)는 까다로운 것으로 판명된다. 집합의 크기를 **측도(measure)**라고 한다. 예를 들어, 이산 집합의 카디널리티(cardinality), $\mathbb{R}$에서 구간의 길이, $\mathbb{R}^{d}$에서 영역의 부피는 모두 측도이다. 집합 연산에 대해 잘 동작하고 추가적으로 Borel $\sigma$-algebra 토폴로지를 갖는 집합을 Borel $\sigma$-algebra라고 한다. Betancourt는 기술적인 문제에 얽매이지 않고 집합론에서 확률 공간을 신중하게 구성하는 방법을 자세히 설명한다; https://tinyurl.com/yb3t6mfd를 참조하라. 더 정확한 구성을 위해서는 Billingsley (1995)와 Jacod and Protter (2004)를 참조하라.

이 책에서는 Borel $\sigma$-algebra에 해당하는 실수 값 확률 변수를 고려한다. $\mathbb{R}^{D}$ 값을 갖는 확률 변수는 실수 값 확률 변수의 벡터로 간주한다.

정의 6.1 (확률 밀도 함수, Probability Density Function). 함수 $f: \mathbb{R}^{D} \rightarrow \mathbb{R}$는 다음을 만족할 때 **확률 밀도 함수(probability density function, pdf)**라고 불린다.

1. $\forall \boldsymbol{x} \in \mathbb{R}^{D}: f(\boldsymbol{x}) \geqslant 0$
2. 적분값이 존재하고

$$\int_{\mathbb{R}^{D}} f(\boldsymbol{x}) \mathrm{d} \boldsymbol{x}=1 .$$

이산 확률 변수의 **확률 질량 함수(probability mass functions, pmf)**의 경우, (6.15)의 적분은 합(6.12)으로 대체된다.

확률 밀도 함수는 음이 아닌(non-negative) 함수이며 적분값이 1인 모든 함수 $f$임을 알 수 있다. 우리는 이 함수 $f$와 확률 변수 $X$를 다음과 같이 연관시킨다.

$$P(a \leqslant X \leqslant b)=\int_{a}^{b} f(x) \mathrm{d} x$$

여기서 $a, b \in \mathbb{R}$이고 $x \in \mathbb{R}$는 연속 확률 변수 $X$의 결과(outcomes)이다. 상태 $\boldsymbol{x} \in \mathbb{R}^{D}$는 $x \in \mathbb{R}$의 벡터를 고려하여 유사하게 정의된다. 이 연관성 (6.16)을 확률 변수 $X$의 법칙(law) 또는 **분포(distribution)**라고 한다.

참고. 이산 확률 변수와 달리, 연속 확률 변수 $X$가 특정 값 $x$를 취할 확률 $P(X=x)$는 0이다. 이는 (6.16)에서 $a=b$인 구간을 지정하려는 것과 같다.

정의 6.2 (누적 분포 함수, Cumulative Distribution Function). 상태 $\boldsymbol{x} \in \mathbb{R}^{D}$를 갖는 다변량 실수 값 확률 변수 $X$의 **누적 분포 함수(cumulative distribution function, cdf)**는 다음과 같이 주어진다.

$$F_{X}(\boldsymbol{x})=P\left(X_{1} \leqslant x_{1}, \ldots, X_{D} \leqslant x_{D}\right),$$

여기서 $X=\left[X_{1}, \ldots, X_{D}\right]^{\top}$, $\boldsymbol{x}=\left[x_{1}, \ldots, x_{D}\right]^{\top}$이며, 우변은 확률 변수 $X_{i}$가 $x_{i}$보다 작거나 같은 값을 취할 확률을 나타낸다.

cdf는 확률 밀도 함수 $f(\boldsymbol{x})$의 적분으로도 표현될 수 있으며, 다음과 같다.

$$F_{X}(\boldsymbol{x})=\int_{-\infty}^{x_{1}} \cdots \int_{-\infty}^{x_{D}} f\left(z_{1}, \ldots, z_{D}\right) \mathrm{d} z_{1} \cdots \mathrm{d} z_{D} .$$

참고. 분포에 대해 이야기할 때 실제로 두 가지 별개의 개념이 있다는 점을 다시 강조한다. 첫째는 pdf($f(x)$로 표기)의 개념으로, 합이 1인 음이 아닌 함수이다. 둘째는 확률 변수 $X$의 법칙(law), 즉 확률 변수 $X$와 pdf $f(x)$의 연관성이다. ©2021 M. P. Deisenroth, A. A. Faisal, C. S. Ong. Published by Cambridge University Press (2020). 확률 밀도 함수(probability density function, pdf) 법칙(law) $P(X=x)$는 측도 0의 집합이다. 누적 분포 함수(cumulative distribution function)

해당하는 pdf가 없는 cdf도 있다. 균등 분포(uniform distribution)

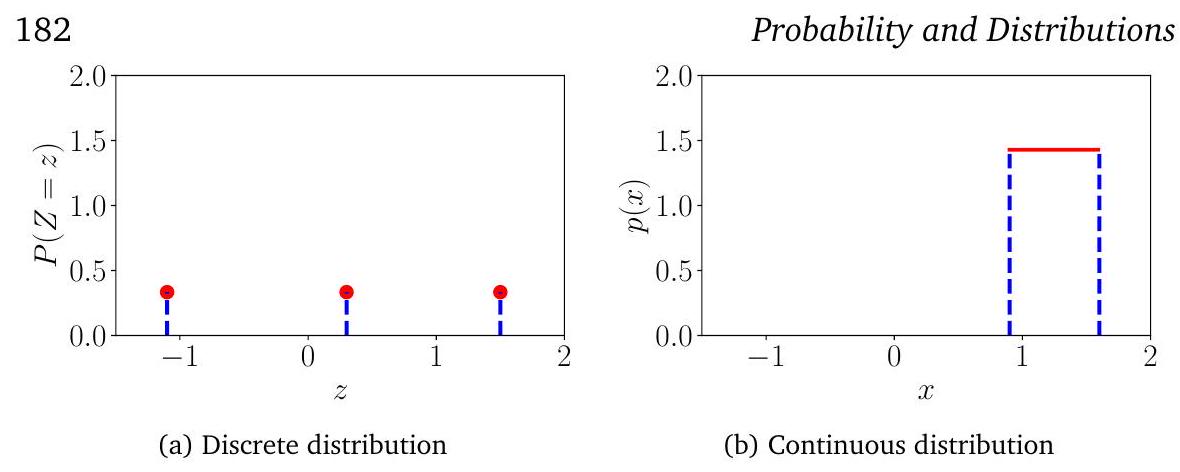
그림 6.3 (a) 이산 균등 분포와 (b) 연속 균등 분포의 예시. 분포에 대한 자세한 내용은 예시 6.3을 참조하라.

이 책의 대부분에서는 pdf와 cdf를 구별할 필요가 없으므로 $f(x)$와 $F_{X}(x)$ 표기법을 사용하지 않을 것이다. 그러나 섹션 6.7에서는 pdf와 cdf에 대해 주의해야 할 것이다.

6.2.3 Contrasting Discrete and Continuous Distributions

6.1.2절에서 확률은 양수이며 총 확률의 합은 1이라는 것을 상기하자. 이산 확률 변수(6.12 참조)의 경우, 이는 각 상태의 확률이 구간 $[0,1]$ 내에 있어야 함을 의미한다. 그러나 연속 확률 변수의 경우, 정규화(6.15 참조)는 밀도 값이 모든 값에 대해 1보다 작거나 같다는 것을 의미하지는 않는다. 우리는 이산 및 연속 확률 변수 모두에 대한 **균등 분포(uniform distribution)**를 사용하여 그림 6.3에서 이를 설명한다.

Example 6.3

각 상태가 동일하게 발생할 가능성이 있는 균등 분포의 두 가지 예를 고려한다. 이 예시는 이산 확률 분포와 연속 확률 분포 간의 몇 가지 차이점을 보여준다.

$Z$를 세 가지 상태 $\{z= -1.1, z=0.3, z=1.5\}$를 갖는 이산 균등 확률 변수라고 하자. **확률 질량 함수(probability mass function)**는 확률 값의 표로 나타낼 수 있다:

$$\begin{array}{c|c|c|c|} z & -1.1 & 0.3 & 1.5 \\ \cline { 2 - 4 } & & \frac{1}{3} & \frac{1}{3} \\ \cline { 2 - 4 } & & & \end{array}$$

또는 이를 그래프(Figure 6.3(a))로 생각할 수도 있는데, 여기서 상태가 $x$축에 위치할 수 있고 $y$축은 특정 상태의 확률을 나타낸다는 사실을 이용한다. Figure 6.3(a)의 $y$축은 Figure 6.3(b)와 동일하도록 의도적으로 확장되었다.

Figure 6.3(b)에 나타낸 바와 같이, $0.9 \leqslant X \leqslant 1.6$ 범위의 값을 취하는 연속 확률 변수 $X$를 가정하자. **밀도(density)**의 높이가 1보다 클 수 있음에 유의하라. 그러나 다음이 성립해야 한다.

$$\int_{0.9}^{1.6} p(x) \mathrm{d} x=1$$

비고. 이산 확률 분포와 관련하여 추가적인 미묘한 차이가 있다. 상태 $z_{1}, \ldots, z_{d}$는 원칙적으로 어떤 구조도 가지지 않는다. 즉, 일반적으로 이들을 비교할 방법이 없다. 예를 들어 $z_{1}=$ red, $z_{2}=$ green, $z_{3}=$ blue와 같은 경우이다. 그러나 많은 머신러닝 애플리케이션에서 이산 상태는 $z_{1}=-1.1, z_{2}= 0.3, z_{3}=1.5$와 같이 수치 값을 취하며, 이 경우 $z_{1}<z_{2}<z_{3}$라고 말할 수 있다. 수치 값을 가정하는 이산 상태는 우리가 종종 확률 변수의 기댓값(expected values)(Section 6.4.1)을 고려하기 때문에 특히 유용하다.

불행히도, 머신러닝 문헌에서는 표본 공간(sample space) $\Omega$, 대상 공간(target space) $\mathcal{T}$, 그리고 확률 변수(random variable) $X$ 사이의 구분을 모호하게 하는 표기법과 명칭을 사용한다. 확률 변수 $X$의 가능한 결과 집합의 값 $x$, 즉 $x \in \mathcal{T}$에 대해 $p(x)$는 확률 변수 $X$가 결과 $x$를 가질 확률을 나타낸다. 이산 확률 변수의 경우, 이는 $P(X=x)$로 쓰이며, **확률 질량 함수(probability mass function)**로 알려져 있다. pmf는 종종 "분포(distribution)"라고 불린다. 연속 변수의 경우, $p(x)$는 확률 밀도 함수(probability density function)(종종 밀도라고 불림)라고 불린다. 상황을 더욱 혼란스럽게 하는 것은, 누적 분포 함수(cumulative distribution function) $P(X \leqslant x)$도 종종 "분포(distribution)"라고 불린다는 점이다. 이 장에서는 단변량 및 다변량 확률 변수 모두를 나타내기 위해 $X$ 표기법을 사용하고, 상태는 각각 $x$와 $\boldsymbol{x}$로 나타낼 것이다. 명칭은 Table 6.1에 요약되어 있다.

Table 6.1 확률 분포에 대한 명칭.

비고. 우리는 "확률 분포(probability distribution)"라는 표현을 이산 확률 질량 함수뿐만 아니라 연속 확률 밀도 함수에도 사용할 것이지만, 이는 기술적으로는 정확하지 않다. 대부분의 머신러닝 문헌과 마찬가지로, 우리는 확률 분포라는 구문의 다양한 용도를 구분하기 위해 문맥에 의존할 것이다.

6.3 Sum Rule, Product Rule, and Bayes' Theorem

우리는 확률론을 논리적 추론의 확장으로 생각한다. 섹션 6.1.1에서 논의했듯이, 여기에 제시된 확률 규칙은 다음을 따른다.

우리는 결과 $x$를 확률 $p(x)$를 초래하는 인수로 생각한다.

이 두 가지 규칙은 섹션 6.1.1에서 논의한 요구 사항으로부터 자연스럽게 발생한다 (Jaynes, 2003).

• 합의 법칙 (sum rule)
• 주변화 속성 (marginalization property)
• 곱의 법칙 (product rule)

이 규칙들은 desiderata (Jaynes, 2003, chapter 2)를 충족함으로써 자연스럽게 도출된다. 확률론적 모델링 (Probabilistic modeling) (섹션 8.4)은 머신러닝 방법을 설계하기 위한 원칙적인 기반을 제공한다. 데이터와 문제의 불확실성에 해당하는 확률 분포 (probability distributions) (섹션 6.2)를 정의하고 나면, **합의 법칙 (sum rule)**과 **곱의 법칙 (product rule)**이라는 두 가지 근본적인 규칙만 존재한다는 것을 알 수 있다.

(6.9)에서 $p(\boldsymbol{x}, \boldsymbol{y})$가 두 확률 변수 $\boldsymbol{x}, \boldsymbol{y}$의 **결합 분포 (joint distribution)**임을 상기하자. 분포 $p(\boldsymbol{x})$와 $p(\boldsymbol{y})$는 해당 **주변 분포 (marginal distributions)**이며, $p(\boldsymbol{y} \mid \boldsymbol{x})$는 $\boldsymbol{x}$가 주어졌을 때 $\boldsymbol{y}$의 **조건부 분포 (conditional distribution)**이다. 섹션 6.2에서 이산 및 연속 확률 변수에 대한 주변 확률과 조건부 확률의 정의를 고려하여, 이제 확률론의 두 가지 근본적인 규칙을 제시할 수 있다.

첫 번째 규칙인 **합의 법칙 (sum rule)**은 다음과 같이 명시한다.

$$p(\boldsymbol{x})=\left\{\begin{array}{ll} \sum_{\boldsymbol{y} \in \mathcal{Y}} p(\boldsymbol{x}, \boldsymbol{y}) & \text { if } \boldsymbol{y} \text { is discrete } \\ \int_{\mathcal{Y}} p(\boldsymbol{x}, \boldsymbol{y}) \mathrm{d} \boldsymbol{y} & \text { if } \boldsymbol{y} \text { is continuous } \end{array},\right.$$

여기서 $\mathcal{Y}$는 확률 변수 $Y$의 목표 공간의 상태이다. 이는 확률 변수 $Y$의 상태 집합 $\boldsymbol{y}$를 합산(또는 적분)한다는 의미이다. **합의 법칙 (sum rule)**은 **주변화 속성 (marginalization property)**으로도 알려져 있다. **합의 법칙 (sum rule)**은 **결합 분포 (joint distribution)**를 **주변 분포 (marginal distribution)**와 연결한다. 일반적으로 **결합 분포 (joint distribution)**가 두 개 이상의 확률 변수를 포함할 때, **합의 법칙 (sum rule)**은 확률 변수의 어떤 부분 집합에도 적용될 수 있으며, 그 결과 하나 이상의 확률 변수의 **주변 분포 (marginal distribution)**를 얻을 수 있다. 더 구체적으로, $\boldsymbol{x}=\left[x_{1}, \ldots, x_{D}\right]^{\top}$인 경우, 우리는 다음 **주변 분포 (marginal)**를 얻는다.

$$p\left(x_{i}\right)=\int p\left(x_{1}, \ldots, x_{D}\right) \mathrm{d} \boldsymbol{x}_{\backslash i}$$

이는 $x_{i}$를 제외한 모든 확률 변수를 적분/합산하는 **합의 법칙 (sum rule)**을 반복적으로 적용함으로써 얻어지며, $\backslash i$는 "i를 제외한 모든 것"을 의미한다. 참고. **확률론적 모델링 (probabilistic modeling)**의 많은 계산적 어려움은 **합의 법칙 (sum rule)**의 적용에서 비롯된다. 변수가 많거나 상태가 많은 이산 변수가 있을 때, **합의 법칙 (sum rule)**은 고차원 합 또는 적분을 수행하는 것으로 귀결된다. 고차원 합 또는 적분을 수행하는 것은 일반적으로 계산적으로 어렵다. 즉, 이를 정확하게 계산하는 알려진 다항 시간 알고리즘이 없다.

**곱의 법칙 (product rule)**으로 알려진 두 번째 규칙은 **결합 분포 (joint distribution)**를 **조건부 분포 (conditional distribution)**와 다음과 같이 연결한다.

$$p(\boldsymbol{x}, \boldsymbol{y})=p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{x}) .$$

**곱의 법칙 (product rule)**은 두 확률 변수의 모든 **결합 분포 (joint distribution)**가 다른 두 분포로 **인수분해 (factorized)**될 수 있다는 사실로 해석될 수 있다. 두 인수는 첫 번째 확률 변수의 주변 분포 (marginal distribution) $p(\boldsymbol{x})$와 첫 번째 확률 변수가 주어졌을 때 두 번째 확률 변수의 조건부 분포 (conditional distribution) $p(\boldsymbol{y} \mid \boldsymbol{x})$이다. $p(\boldsymbol{x}, \boldsymbol{y})$에서 확률 변수의 순서는 임의적이므로, **곱의 법칙 (product rule)**은 또한 $p(\boldsymbol{x}, \boldsymbol{y})=p(\boldsymbol{x} \mid \boldsymbol{y}) p(\boldsymbol{y})$를 의미한다. 정확히 말하면, (6.22)는 이산 확률 변수에 대한 **확률 질량 함수 (probability mass functions)**로 표현된다. 연속 확률 변수의 경우, **곱의 법칙 (product rule)**은 확률 밀도 함수 (probability density functions) (섹션 6.2.3)로 표현된다.

머신러닝과 베이즈 통계학에서 우리는 다른 확률 변수를 관찰했을 때 관찰되지 않은 (잠재) 확률 변수에 대한 추론을 하는 데 종종 관심이 있다. 관찰되지 않은 확률 변수 $\boldsymbol{x}$에 대한 사전 지식 (prior knowledge) $p(\boldsymbol{x})$와 $\boldsymbol{x}$와 우리가 관찰할 수 있는 두 번째 확률 변수 $\boldsymbol{y}$ 사이의 관계 $p(\boldsymbol{y} \mid \boldsymbol{x})$가 있다고 가정하자. $\boldsymbol{y}$를 관찰하면, **베이즈 정리 (Bayes' theorem)**를 사용하여 관찰된 $\boldsymbol{y}$ 값에 따라 $\boldsymbol{x}$에 대한 결론을 도출할 수 있다. 베이즈 정리 (Bayes' theorem) (또는 베이즈 규칙 (Bayes' rule) 또는 베이즈 법칙 (Bayes' law))

$$\underbrace{p(\boldsymbol{x} \mid \boldsymbol{y})}_{\text {posterior }}=\frac{\overbrace{p(\boldsymbol{y} \mid \boldsymbol{x})}^{\text {likelihood }} \overbrace{p(\boldsymbol{x})}^{\text {prior }}}{\underbrace{p(\boldsymbol{y})}_{\text {evidence }}}$$

는 (6.22)의 **곱의 법칙 (product rule)**의 직접적인 결과이다. 왜냐하면

$$p(\boldsymbol{x}, \boldsymbol{y})=p(\boldsymbol{x} \mid \boldsymbol{y}) p(\boldsymbol{y})$$

이고

$$p(\boldsymbol{x}, \boldsymbol{y})=p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{x})$$

이므로

$$p(\boldsymbol{x} \mid \boldsymbol{y}) p(\boldsymbol{y})=p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{x}) \Longleftrightarrow p(\boldsymbol{x} \mid \boldsymbol{y})=\frac{p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{x})}{p(\boldsymbol{y})} .$$

(6.23)에서 $p(\boldsymbol{x})$는 **사전 분포 (prior)**이며, 이는 데이터를 관찰하기 전의 관찰되지 않은 (잠재) 변수 $\boldsymbol{x}$에 대한 우리의 주관적인 **사전 지식 (prior knowledge)**을 요약한다. 우리는 우리에게 합리적인 어떤 **사전 분포 (prior)**도 선택할 수 있지만, **사전 분포 (prior)**가 모든 그럴듯한 $\boldsymbol{x}$에 대해 0이 아닌 pdf (또는 pmf)를 갖도록 하는 것이 중요하다. 비록 그것들이 매우 드물더라도 말이다.

우도 (likelihood) $p(\boldsymbol{y} \mid \boldsymbol{x})$는 $\boldsymbol{x}$와 $\boldsymbol{y}$가 어떻게 관련되어 있는지를 설명하며, 이산 확률 분포의 경우, 잠재 변수 $\boldsymbol{x}$를 안다면 데이터 $\boldsymbol{y}$의 확률이다. **우도 (likelihood)**는 $\boldsymbol{x}$에 대한 분포가 아니라 $\boldsymbol{y}$에 대한 분포라는 점에 유의하라. 우리는 $p(\boldsymbol{y} \mid \boldsymbol{x})$를 "$\boldsymbol{x}$의 우도 (likelihood) ($\boldsymbol{y}$가 주어졌을 때)" 또는 "$\boldsymbol{x}$가 주어졌을 때 $\boldsymbol{y}$의 확률"이라고 부르지만, 결코 "$\boldsymbol{y}$의 우도 (likelihood)"라고 부르지 않는다 (MacKay, 2003).

사후 분포 (posterior) $p(\boldsymbol{x} \mid \boldsymbol{y})$는 베이즈 통계학에서 관심 있는 양이다. 왜냐하면 이는 우리가 관심 있는 것, 즉 $\boldsymbol{y}$를 관찰한 후 $\boldsymbol{x}$에 대해 우리가 아는 것을 정확하게 표현하기 때문이다.

• 베이즈 정리 (Bayes' theorem)
• 베이즈 규칙 (Bayes' rule)
• 베이즈 법칙 (Bayes' law)
• 사전 분포 (prior)
• 우도 (likelihood): **우도 (likelihood)**는 때때로 "측정 모델 (measurement model)"이라고도 불린다.
• 사후 분포 (posterior)

다음 양

$$p(\boldsymbol{y}):=\int p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x}=\mathbb{E}_{X}[p(\boldsymbol{y} \mid \boldsymbol{x})]$$

• 주변 우도 (marginal likelihood)
• 증거 (evidence)

**베이즈 정리 (Bayes' theorem)**는 "확률론적 역변환 (probabilistic inverse)"이라고도 불린다. 는 주변 우도 (marginal likelihood)/**증거 (evidence)**이다. (6.27)의 우변은 섹션 6.4.1에서 정의할 **기대 연산자 (expectation operator)**를 사용한다. 정의에 따르면, **주변 우도 (marginal likelihood)**는 (6.23)의 분자를 잠재 변수 $\boldsymbol{x}$에 대해 적분한다. 따라서 **주변 우도 (marginal likelihood)**는 $\boldsymbol{x}$와 독립적이며, 사후 분포 (posterior) $p(\boldsymbol{x} \mid \boldsymbol{y})$가 정규화되도록 보장한다. **주변 우도 (marginal likelihood)**는 사전 분포 (prior) $p(\boldsymbol{x})$에 대한 기대를 취하는 **기대 우도 (expected likelihood)**로도 해석될 수 있다. **사후 분포 (posterior)**의 정규화 외에도, **주변 우도 (marginal likelihood)**는 섹션 8.6에서 논의할 **베이즈 모델 선택 (Bayesian model selection)**에서도 중요한 역할을 한다. (8.44)의 적분 때문에 **증거 (evidence)**는 종종 계산하기 어렵다.

베이즈 정리 (Bayes' theorem) (6.23)은 **우도 (likelihood)**에 의해 주어진 $\boldsymbol{x}$와 $\boldsymbol{y}$ 사이의 관계를 역전시킬 수 있게 한다. 따라서 **베이즈 정리 (Bayes' theorem)**는 때때로 **확률론적 역변환 (probabilistic inverse)**이라고 불린다. 우리는 섹션 8.4에서 **베이즈 정리 (Bayes' theorem)**를 더 자세히 논의할 것이다. 참고. 베이즈 통계학에서 **사후 분포 (posterior distribution)**는 **사전 분포 (prior)**와 데이터로부터 얻을 수 있는 모든 정보를 요약하므로 관심 있는 양이다. **사후 분포 (posterior)**를 그대로 사용하는 대신, 섹션 8.3에서 논의할 **사후 분포 (posterior)**의 최댓값과 같은 **사후 분포 (posterior)**의 일부 통계량에 집중할 수 있다. 그러나 **사후 분포 (posterior)**의 일부 통계량에 집중하는 것은 정보 손실로 이어진다. 더 큰 맥락에서 생각하면, **사후 분포 (posterior)**는 의사 결정 시스템 내에서 사용될 수 있으며, 전체 **사후 분포 (posterior)**를 갖는 것은 매우 유용하며 교란에 강건한 결정을 내릴 수 있다. 예를 들어, **모델 기반 강화 학습 (model-based reinforcement learning)**의 맥락에서 Deisenroth et al. (2015)은 그럴듯한 **전이 함수 (transition functions)**의 전체 **사후 분포 (posterior distribution)**를 사용하는 것이 매우 빠른 (데이터/샘플 효율적인) 학습으로 이어지는 반면, **사후 분포 (posterior)**의 최댓값에 집중하는 것은 일관된 실패로 이어진다는 것을 보여준다. 따라서 전체 **사후 분포 (posterior)**를 갖는 것은 다운스트림 task에 매우 유용할 수 있다. 챕터 9에서는 **선형 회귀 (linear regression)**의 맥락에서 이 논의를 계속할 것이다.

6.4 Summary Statistics and Independence

우리는 종종 확률 변수 집합을 요약하고 확률 변수 쌍을 비교하는 데 관심을 갖는다. 확률 변수의 **통계량(statistic)**은 해당 확률 변수의 **결정론적 함수(deterministic function)**이다. 분포의 **요약 통계량(summary statistics)**은 확률 변수가 어떻게 동작하는지에 대한 유용한 관점을 제공하며, 이름에서 알 수 있듯이 분포를 요약하고 특징짓는 숫자를 제공한다. 우리는 잘 알려진 두 가지 요약 통계량인 **평균(mean)**과 **분산(variance)**을 설명한다. 그런 다음 확률 변수 쌍을 비교하는 두 가지 방법을 논의한다. 첫째, 두 확률 변수가 **독립적(independent)**이라고 말하는 방법, 둘째, 두 확률 변수 사이의 **내적(inner product)**을 계산하는 방법이다.

6.4.1 Means and Covariances

평균과 (공)분산은 확률 분포의 속성(기댓값과 퍼짐)을 설명하는 데 유용하게 사용된다. 섹션 6.6에서 우리는 확률 변수의 통계량이 가능한 모든 정보를 포착하는 유용한 분포군(exponential family라고 불림)이 있다는 것을 알게 될 것이다.

기댓값의 개념은 머신러닝의 핵심이며, 확률 자체의 기초 개념은 기댓값에서 파생될 수 있다 (Whittle, 2000).

정의 6.3 (기댓값). 단변량 연속 확률 변수 $X \sim p(x)$의 함수 $g: \mathbb{R} \rightarrow \mathbb{R}$의 기댓값은 다음과 같이 주어진다.

$$\mathbb{E}_{X}[g(x)]=\int_{\mathcal{X}} g(x) p(x) \mathrm{d} x .$$

마찬가지로, 이산 확률 변수 $X \sim p(x)$의 함수 $g$의 기댓값은 다음과 같이 주어진다.

$$\mathbb{E}_{X}[g(x)]=\sum_{x \in \mathcal{X}} g(x) p(x)$$

여기서 $\mathcal{X}$는 확률 변수 $X$의 가능한 결과들의 집합(대상 공간)이다.

이 섹션에서는 이산 확률 변수가 수치적 결과를 갖는다고 가정한다. 이는 함수 $g$가 실수를 입력으로 받는다는 것을 관찰함으로써 알 수 있다.

참고. 우리는 다변량 확률 변수 $X$를 단변량 확률 변수 $\left[X_{1}, \ldots, X_{D}\right]^{\top}$의 유한 벡터로 간주한다. 다변량 확률 변수의 경우, 기댓값을 요소별로 정의한다.

$$\mathbb{E}_{X}[g(\boldsymbol{x})]=\left[\begin{array}{c} \mathbb{E}_{X_{1}}\left[g\left(x_{1}\right)\right] \\ \vdots \\ \mathbb{E}_{X_{D}}\left[g\left(x_{D}\right)\right] \end{array}\right] \in \mathbb{R}^{D},$$

여기서 아래 첨자 $\mathbb{E}_{X_{d}}$는 벡터 $\boldsymbol{x}$의 $d$번째 요소에 대한 기댓값을 취하고 있음을 나타낸다.

정의 6.3은 $\mathbb{E}_{X}$ 표기법의 의미를 확률 밀도에 대한 적분(연속 분포의 경우) 또는 모든 상태에 대한 합(이산 분포의 경우)을 취해야 함을 나타내는 연산자로 정의한다. 평균의 정의(정의 6.4)는 기댓값의 특수한 경우로, $g$를 항등 함수로 선택하여 얻어진다.

정의 6.4 (평균). 상태가 $\boldsymbol{x} \in \mathbb{R}^{D}$인 확률 변수 $X$의 평균은 평균이며 다음과 같이 정의된다.

$$\mathbb{E}_{X}[\boldsymbol{x}]=\left[\begin{array}{c} \mathbb{E}_{X_{1}}\left[x_{1}\right] \\ \vdots \\ \mathbb{E}_{X_{D}}\left[x_{D}\right] \end{array}\right] \in \mathbb{R}^{D}$$

여기서 $\mathbb{E}_{X_{d}}\left[x_{d}\right]:= \begin{cases}\int_{\mathcal{X}} x_{d} p\left(x_{d}\right) \mathrm{d} x_{d} & \text { if } X \text { is a continuous random variable } \\ \sum_{x_{i} \in \mathcal{X}} x_{i} p\left(x_{d}=x_{i}\right) & \text { if } X \text { is a discrete random variable }\end{cases}$ $d=1, \ldots, D$에 대해, 아래 첨자 $d$는 $\boldsymbol{x}$의 해당 차원을 나타낸다. 적분과 합은 확률 변수 $X$의 대상 공간의 상태 $\mathcal{X}$에 대한 것이다.

1차원에서는 "평균"에 대한 두 가지 다른 직관적인 개념이 있는데, 바로 **중앙값(median)**과 **최빈값(mode)**이다. 중앙값은 값을 정렬했을 때 "중간" 값, 즉 값의 50%는 중앙값보다 크고 50%는 중앙값보다 작다. 이 아이디어는 cdf(정의 6.2)가 0.5인 값을 고려하여 연속 값으로 일반화될 수 있다. 비대칭이거나 긴 꼬리를 가진 분포의 경우, 중앙값은 평균값보다 인간의 직관에 더 가까운 전형적인 값의 추정치를 제공한다. 또한, 중앙값은 평균보다 이상치(outlier)에 더 강건하다. 중앙값을 고차원으로 일반화하는 것은 비자명한데, 이는 1차원 이상에서는 "정렬"하는 명확한 방법이 없기 때문이다 (Hallin et al., 2010; Kong and Mizera, 2012). 최빈값은 가장 자주 발생하는 값이다. 이산 확률 변수의 경우, 최빈값은 가장 높은 발생 빈도를 갖는 $x$ 값으로 정의된다. 연속 확률 변수의 경우, 최빈값은 밀도 $p(\boldsymbol{x})$의 **피크(peak)**로 정의된다. 특정 밀도 $p(\boldsymbol{x})$는 하나 이상의 최빈값을 가질 수 있으며, 고차원 분포에서는 매우 많은 수의 최빈값이 있을 수도 있다. 따라서 분포의 모든 최빈값을 찾는 것은 계산적으로 어려울 수 있다.

Example 6.4

그림 6.4에 나타난 2차원 분포를 고려해 보자:

$$p(x)=0.4 \mathcal{N}\left(\boldsymbol{x} \left\lvert\,\left[\begin{array}{c} 10 \\ 2 \end{array}\right]\right.,\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\right)+0.6 \mathcal{N}\left(\boldsymbol{x} \left\lvert\,\left[\begin{array}{l} 0 \\ 0 \end{array}\right]\right.,\left[\begin{array}{ll} 8.4 & 2.0 \\ 2.0 & 1.7 \end{array}\right]\right)$$

우리는 섹션 6.5에서 가우시안 분포 $\mathcal{N}\left(\mu, \sigma^{2}\right)$를 정의할 것이다. 또한 각 차원의 해당 marginal 분포도 함께 나타나 있다. 이 분포는 bimodal(두 개의 mode를 가짐)이지만, marginal 분포 중 하나는 unimodal(하나의 mode를 가짐)임을 알 수 있다. 수평 bimodal univariate 분포는 **평균(mean)**과 **중앙값(median)**이 서로 다를 수 있음을 보여준다. 2차원 중앙값을 각 차원의 중앙값을 연결한 것으로 정의하고 싶지만, 2차원 점들의 순서를 정의할 수 없다는 사실이 이를 어렵게 만든다. "순서를 정의할 수 없다"는 것은 $\left[\begin{array}{l}3 \\ 0\end{array}\right]<\left[\begin{array}{l}2 \\ 3\end{array}\right]$와 같이 관계 $<$를 정의하는 방법이 한 가지 이상 존재한다는 것을 의미한다.

그림 6.4 2차원 데이터셋의 평균(mean), 최빈값(mode), 중앙값(median) 및 marginal 밀도를 보여주는 그림.

비고. 기댓값(expected value)(정의 6.3)은 **선형 연산자(linear operator)**이다. 예를 들어, $a, b \in \mathbb{R}$이고 $\boldsymbol{x} \in \mathbb{R}^{D}$인 실수 값 함수 $f(\boldsymbol{x})=a g(\boldsymbol{x})+b h(\boldsymbol{x})$가 주어졌을 때, 우리는 다음을 얻는다.

$$\begin{aligned} \mathbb{E}_{X}[f(\boldsymbol{x})] & =\int f(\boldsymbol{x}) p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x} \\ & =\int[a g(\boldsymbol{x})+b h(\boldsymbol{x})] p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x} \\ & =a \int g(\boldsymbol{x}) p(\boldsymbol{x}) \mathrm{d} x+b \int h(\boldsymbol{x}) p(\boldsymbol{x}) \mathrm{d} \boldsymbol{x} \\ & =a \mathbb{E}_{X}[g(\boldsymbol{x})]+b \mathbb{E}_{X}[h(\boldsymbol{x})] \end{aligned}$$

두 확률 변수에 대해 우리는 그들의 상응하는 **공분산(covariance)**을 특성화하고자 할 수 있다.

용어: 다변량 확률 변수의 공분산 $\operatorname{Cov}[x, y]$은 때때로 **교차 공분산(cross-covariance)**이라고 불리며, 공분산은 $\operatorname{Cov}[x, x]$를 지칭한다. 분산(variance) 표준 편차(standard deviation) 공분산(covariance) 분산(variance) 공분산 행렬(covariance matrix) marginal 공분산은 확률 변수들이 서로 얼마나 의존적인지에 대한 개념을 직관적으로 나타낸다.

정의 6.5 (공분산(단변량)). 두 단변량 확률 변수 $X, Y \in \mathbb{R}$ 사이의 공분산은 각각의 평균으로부터의 편차의 기댓값으로 주어진다. 즉,

$$\operatorname{Cov}_{X, Y}[x, y]:=\mathbb{E}_{X, Y}\left[\left(x-\mathbb{E}_{X}[x]\right)\left(y-\mathbb{E}_{Y}[y]\right)\right] .$$

비고. 기댓값 또는 공분산과 관련된 확률 변수가 인수에 의해 명확할 경우, 아래 첨자는 종종 생략된다(예를 들어, $\mathbb{E}_{X}[x]$는 종종 $\mathbb{E}[x]$로 쓰인다).

기댓값의 선형성을 사용하면, 정의 6.5의 표현은 곱의 기댓값에서 기댓값의 곱을 뺀 것으로 다시 쓸 수 있다. 즉,

$$\operatorname{Cov}[x, y]=\mathbb{E}[x y]-\mathbb{E}[x] \mathbb{E}[y] .$$

변수 자신과의 공분산 $\operatorname{Cov}[x, x]$은 분산이라고 불리며 $\mathbb{V}_{X}[x]$로 표기된다. 분산의 제곱근은 표준 편차라고 불리며 종종 $\sigma(x)$로 표기된다. 공분산의 개념은 다변량 확률 변수로 일반화될 수 있다.

정의 6.6 (공분산(다변량)). 상태가 각각 $\boldsymbol{x} \in \mathbb{R}^{D}$ 및 $\boldsymbol{y} \in \mathbb{R}^{E}$인 두 다변량 확률 변수 $X$와 $Y$를 고려할 때, $X$와 $Y$ 사이의 공분산은 다음과 같이 정의된다.

$$\operatorname{Cov}[\boldsymbol{x}, \boldsymbol{y}]=\mathbb{E}\left[\boldsymbol{x} \boldsymbol{y}^{\top}\right]-\mathbb{E}[\boldsymbol{x}] \mathbb{E}[\boldsymbol{y}]^{\top}=\operatorname{Cov}[\boldsymbol{y}, \boldsymbol{x}]^{\top} \in \mathbb{R}^{D \times E} .$$

정의 6.6은 두 인수에 동일한 다변량 확률 변수를 적용하여 확률 변수의 "분포"를 직관적으로 포착하는 유용한 개념을 도출할 수 있다. 다변량 확률 변수의 경우, 분산은 확률 변수의 개별 차원 간의 관계를 설명한다.

정의 6.7 (분산). 상태가 $\boldsymbol{x} \in \mathbb{R}^{D}$이고 평균 벡터가 $\boldsymbol{\mu} \in \mathbb{R}^{D}$인 확률 변수 $X$의 분산은 다음과 같이 정의된다.

$$\begin{aligned} \mathbb{V}_{X}[\boldsymbol{x}] & =\operatorname{Cov}_{X}[\boldsymbol{x}, \boldsymbol{x}] \\ & =\mathbb{E}_{X}\left[(\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^{\top}\right]=\mathbb{E}_{X}\left[\boldsymbol{x} \boldsymbol{x}^{\top}\right]-\mathbb{E}_{X}[\boldsymbol{x}] \mathbb{E}_{X}[\boldsymbol{x}]^{\top} \\ & =\left[\begin{array}{cccc} \operatorname{Cov}\left[x_{1}, x_{1}\right] & \operatorname{Cov}\left[x_{1}, x_{2}\right] & \ldots & \operatorname{Cov}\left[x_{1}, x_{D}\right] \\ \operatorname{Cov}\left[x_{2}, x_{1}\right] & \operatorname{Cov}\left[x_{2}, x_{2}\right] & \ldots & \operatorname{Cov}\left[x_{2}, x_{D}\right] \\ \vdots & \vdots & \ddots & \vdots \\ \operatorname{Cov}\left[x_{D}, x_{1}\right] & \ldots & \ldots & \operatorname{Cov}\left[x_{D}, x_{D}\right] \end{array}\right] \end{aligned}$$

(6.38c)의 $D \times D$ 행렬은 다변량 확률 변수 $X$의 공분산 행렬이라고 불린다. 공분산 행렬은 **대칭(symmetric)**이며 **양의 준정부호(positive semidefinite)**이며 데이터의 분포에 대해 알려준다. 공분산 행렬의 대각선에는 marginal의 분산이 포함되어 있다. 6.4 요약 통계량 및 독립성 (a) $x$와 $y$는 음의 상관관계를 가진다.

그림 6.5 각 축을 따라 동일한 평균과 분산(색상 선)을 가지지만 공분산이 다른 2차원 데이터셋.

(b) $x$와 $y$는 양의 상관관계를 가진다.

$$p\left(x_{i}\right)=\int p\left(x_{1}, \ldots, x_{D}\right) \mathrm{d} x_{\backslash i}$$

여기서 "$\backslash i$"는 "$i$를 제외한 모든 변수"를 의미한다. 비대각선 항목은 $i, j=1, \ldots, D, i \neq j$에 대한 교차 공분산 항 $\operatorname{Cov}\left[x_{i}, x_{j}\right]$이다. 비고. 이 책에서는 일반적으로 더 나은 직관을 위해 공분산 행렬이 **양의 정부호(positive definite)**라고 가정한다. 따라서 양의 준정부호(positive semidefinite)(저랭크) 공분산 행렬을 초래하는 특이한 경우는 다루지 않는다.

서로 다른 확률 변수 쌍 간의 공분산을 비교하고자 할 때, 각 확률 변수의 분산이 공분산 값에 영향을 미친다는 것이 밝혀졌다. 공분산의 정규화된 버전은 **상관관계(correlation)**라고 불린다.

정의 6.8 (상관관계). 두 확률 변수 $X, Y$ 사이의 상관관계는 다음과 같이 주어진다.

$$\operatorname{corr}[x, y]=\frac{\operatorname{Cov}[x, y]}{\sqrt{\mathbb{V}[x] \mathbb{V}[y]}} \in[-1,1] .$$

**상관 행렬(correlation matrix)**은 표준화된 확률 변수 $x / \sigma(x)$의 공분산 행렬이다. 다시 말해, 상관 행렬에서는 각 확률 변수가 표준 편차(분산의 제곱근)로 나누어진다.

공분산(상관관계)은 두 확률 변수가 어떻게 관련되어 있는지를 나타낸다. 그림 6.5를 참조하라. 양의 상관관계 $\operatorname{corr}[x, y]$는 $x$가 증가할 때 $y$도 증가할 것으로 예상됨을 의미한다. 음의 상관관계는 $x$가 증가할 때 $y$가 감소함을 의미한다.

6.4.2 Empirical Means and Covariances

섹션 6.4.1의 정의들은 모집단에 대한 **진정한 통계량(true statistics)**을 나타내므로 종종 모집단 평균(population mean) 및 **공분산(covariance)**이라고도 불린다. 머신러닝에서는 데이터의 **경험적 관측치(empirical observations)**로부터 학습해야 한다. 확률 변수 $X$를 고려할 때, 모집단 통계량에서 경험적 통계량의 실현으로 나아가는 두 가지 개념적 단계가 있다.

첫째, 우리는 유한한 데이터셋(크기 $N$)을 가지고 있다는 사실을 이용하여 유한한 수의 동일한 확률 변수 $X_{1}, \ldots, X_{N}$의 함수인 **경험적 통계량(empirical statistic)**을 구성한다. 둘째, 우리는 데이터를 관측한다. 즉, 각 확률 변수의 실현 $x_{1}, \ldots, x_{N}$을 살펴보고 경험적 통계량을 적용한다.

특히, 평균(정의 6.4)의 경우, 특정 데이터셋이 주어졌을 때 평균의 추정치를 얻을 수 있는데, 이를 경험적 평균(empirical mean) 또는 **표본 평균(sample mean)**이라고 한다. 경험적 공분산도 마찬가지이다.

정의 6.9 (경험적 평균 및 공분산). **경험적 평균 벡터(empirical mean vector)**는 각 변수에 대한 관측치의 산술 평균이며 다음과 같이 정의된다.

$$\overline{\boldsymbol{x}}:=\frac{1}{N} \sum_{n=1}^{N} \boldsymbol{x}_{n},$$

여기서 $\boldsymbol{x}_{n} \in \mathbb{R}^{D}$이다. 경험적 평균과 유사하게, **경험적 공분산 행렬(empirical covariance matrix)**은 $D \times D$ 행렬이며 다음과 같다.

$$\boldsymbol{\Sigma}:=\frac{1}{N} \sum_{n=1}^{N}\left(\boldsymbol{x}_{n}-\overline{\boldsymbol{x}}\right)\left(\boldsymbol{x}_{n}-\overline{\boldsymbol{x}}\right)^{\top}$$

특정 데이터셋에 대한 통계량을 계산하기 위해, 우리는 실현(관측치) $\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{N}$을 사용하고 (6.41) 및 (6.42)를 활용할 것이다. 경험적 공분산 행렬은 대칭이며 양의 준정부호(positive semidefinite)이다(섹션 3.2.3 참조).

이 책 전반에 걸쳐 우리는 **편향된 추정치(biased estimate)**인 **경험적 공분산(empirical covariance)**을 사용한다. 비편향(unbiased) (때로는 **수정된(corrected)**이라고도 불리는) 공분산은 분모에 $N$ 대신 $N-1$을 사용한다. 유도는 이 장의 마지막에 있는 연습 문제이다.

6.4.3 Three Expressions for the Variance

이제 단일 확률 변수 $X$에 초점을 맞추고, 앞서 언급된 경험적 공식을 사용하여 분산에 대한 세 가지 가능한 표현을 도출한다. 다음 유도는 모집단 분산에 대해서도 동일하게 적용되지만, 적분을 고려해야 한다는 점이 다르다. 공분산의 정의(정의 6.5)에 해당하는 분산의 표준 정의는 확률 변수 $X$와 그 기댓값 $\mu$의 제곱 편차에 대한 기댓값이다. 즉,

$$\mathbb{V}_{X}[x]:=\mathbb{E}_{X}\left[(x-\mu)^{2}\right]$$

(6.43)의 기댓값과 평균 $\mu=\mathbb{E}_{X}(x)$는 $X$가 이산 확률 변수인지 연속 확률 변수인지에 따라 (6.32)를 사용하여 계산된다. (6.43)에 표현된 분산은 새로운 확률 변수 $Z:=(X-\mu)^{2}$의 평균이다.

(6.43)의 분산을 경험적으로 추정할 때, two-pass algorithm을 사용해야 한다: 첫 번째 pass에서는 (6.41)을 사용하여 평균 $\mu$를 계산하고, 두 번째 pass에서는 이 추정치 $\hat{\mu}$를 사용하여 분산을 계산한다. 하지만 항들을 재배열함으로써 두 번의 pass를 피할 수 있다는 것이 밝혀졌다. (6.43)의 공식은 분산에 대한 소위 raw-score formula로 변환될 수 있다:

$$\mathbb{V}_{X}[x]=\mathbb{E}_{X}\left[x^{2}\right]-\left(\mathbb{E}_{X}[x]\right)^{2} .$$

(6.44)의 표현은 "제곱의 평균에서 평균의 제곱을 뺀 것"으로 기억할 수 있다. 이는 데이터를 한 번만 통과하여 경험적으로 계산할 수 있는데, $i$번째 관측치인 $x_i$와 $x_i^2$를 동시에 누적할 수 있기 때문이다. 불행히도, 이러한 방식으로 구현하면 수치적으로 불안정할 수 있다. 분산의 raw-score 버전은 머신러닝에서, 예를 들어 bias-variance decomposition을 유도할 때 유용할 수 있다 (Bishop, 2006).

분산을 이해하는 세 번째 방법은 모든 관측치 쌍 간의 pairwise difference의 합이라는 것이다. 확률 변수 $X$의 실현값 표본 $x_1, \ldots, x_N$을 고려하고, $x_i$와 $x_j$ 쌍 간의 제곱 차이를 계산한다. 제곱을 전개함으로써, $N^2$개의 pairwise difference의 합이 관측치의 경험적 분산임을 보일 수 있다:

$$\frac{1}{N^{2}} \sum_{i, j=1}^{N}\left(x_{i}-x_{j}\right)^{2}=2\left[\frac{1}{N} \sum_{i=1}^{N} x_{i}^{2}-\left(\frac{1}{N} \sum_{i=1}^{N} x_{i}\right)^{2}\right] .$$

(6.45)가 raw-score 표현 (6.44)의 두 배임을 알 수 있다. 이는 **pairwise distance의 합($N^2$개)**을 **평균으로부터의 편차의 합($N$개)**으로 표현할 수 있음을 의미한다. 기하학적으로, 이는 pairwise distance와 점 집합의 중심으로부터의 거리 사이에 등가성이 있음을 의미한다. 계산 관점에서, 이는 평균을 계산하고(합계에 $N$개의 항), 분산을 계산함으로써(다시 합계에 $N$개의 항), $N^2$개의 항을 갖는 표현((6.45)의 좌변)을 얻을 수 있음을 의미한다.

6.4.4 Sums and Transformations of Random Variables

교과서적인 분포(일부 내용은 섹션 6.5 및 6.6에서 소개)로는 잘 설명되지 않는 현상을 모델링해야 할 수도 있으며, 따라서 확률 변수의 간단한 조작(예: 두 확률 변수 더하기)을 수행할 수 있다.

상태가 $\boldsymbol{x}, \boldsymbol{y} \in \mathbb{R}^{D}$인 두 확률 변수 $X, Y$를 고려하자. 그러면:

$$\begin{aligned} \mathbb{E}[\boldsymbol{x}+\boldsymbol{y}] & =\mathbb{E}[\boldsymbol{x}]+\mathbb{E}[\boldsymbol{y}] \\ \mathbb{E}[\boldsymbol{x}-\boldsymbol{y}] & =\mathbb{E}[\boldsymbol{x}]-\mathbb{E}[\boldsymbol{y}] \\ \mathbb{V}[\boldsymbol{x}+\boldsymbol{y}] & =\mathbb{V}[\boldsymbol{x}]+\mathbb{V}[\boldsymbol{y}]+\operatorname{Cov}[\boldsymbol{x}, \boldsymbol{y}]+\operatorname{Cov}[\boldsymbol{y}, \boldsymbol{x}] \\ \mathbb{V}[\boldsymbol{x}-\boldsymbol{y}] & =\mathbb{V}[\boldsymbol{x}]+\mathbb{V}[\boldsymbol{y}]-\operatorname{Cov}[\boldsymbol{x}, \boldsymbol{y}]-\operatorname{Cov}[\boldsymbol{y}, \boldsymbol{x}] . \end{aligned}$$

분산에 대한 raw-score 공식

(6.44)의 두 항이 매우 크고 거의 같다면, 부동 소수점 연산에서 불필요한 수치 정밀도 손실을 겪을 수 있다.

평균과 (공)분산은 확률 변수의 **아핀 변환(affine transformation)**에 있어서 몇 가지 유용한 속성을 나타낸다. 평균이 $\boldsymbol{\mu}$이고 공분산 행렬이 $\boldsymbol{\Sigma}$인 확률 변수 $X$와 $\boldsymbol{x}$의 (결정론적) 아핀 변환 $\boldsymbol{y}=\boldsymbol{A} \boldsymbol{x}+\boldsymbol{b}$를 고려하자. 그러면 $\boldsymbol{y}$는 그 자체로 확률 변수이며, 평균 벡터와 공분산 행렬은 다음과 같이 주어진다.

$$\begin{aligned} \mathbb{E}_{Y}[\boldsymbol{y}] & =\mathbb{E}_{X}[\boldsymbol{A} \boldsymbol{x}+\boldsymbol{b}]=\boldsymbol{A} \mathbb{E}_{X}[\boldsymbol{x}]+\boldsymbol{b}=\boldsymbol{A} \boldsymbol{\mu}+\boldsymbol{b} \\ \mathbb{V}_{Y}[\boldsymbol{y}] & =\mathbb{V}_{X}[\boldsymbol{A} \boldsymbol{x}+\boldsymbol{b}]=\mathbb{V}_{X}[\boldsymbol{A} \boldsymbol{x}]=\boldsymbol{A} \mathbb{V}_{X}[\boldsymbol{x}] \boldsymbol{A}^{\top}=\boldsymbol{A} \boldsymbol{\Sigma} \boldsymbol{A}^{\top} \end{aligned}$$

이는 평균과 공분산의 정의를 직접 사용하여 보일 수 있다. 통계적 독립성 각각. 또한,

$$\begin{aligned} \operatorname{Cov}[\boldsymbol{x}, \boldsymbol{y}] & =\mathbb{E}\left[\boldsymbol{x}(\boldsymbol{A} \boldsymbol{x}+\boldsymbol{b})^{\top}\right]-\mathbb{E}[\boldsymbol{x}] \mathbb{E}[\boldsymbol{A} \boldsymbol{x}+\boldsymbol{b}]^{\top} \\ & =\mathbb{E}[\boldsymbol{x}] \boldsymbol{b}^{\top}+\mathbb{E}\left[\boldsymbol{x} \boldsymbol{x}^{\top}\right] \boldsymbol{A}^{\top}-\boldsymbol{\mu} \boldsymbol{b}^{\top}-\boldsymbol{\mu} \boldsymbol{\mu}^{\top} \boldsymbol{A}^{\top} \\ & =\boldsymbol{\mu} \boldsymbol{b}^{\top}-\boldsymbol{\mu} \boldsymbol{b}^{\top}+\left(\mathbb{E}\left[\boldsymbol{x} \boldsymbol{x}^{\top}\right]-\boldsymbol{\mu} \boldsymbol{\mu}^{\top}\right) \boldsymbol{A}^{\top} \\ & \stackrel{\text { (6.38b) }}{=} \boldsymbol{\Sigma} \boldsymbol{A}^{\top} \end{aligned}$$

여기서 $\boldsymbol{\Sigma}=\mathbb{E}\left[\boldsymbol{x} \boldsymbol{x}^{\top}\right]-\boldsymbol{\mu} \boldsymbol{\mu}^{\top}$는 $X$의 공분산이다.

6.4.5 Statistical Independence

정의 6.10 (독립성). 두 확률 변수 $X, Y$는 다음을 만족할 때 통계적으로 독립이다.

$$p(\boldsymbol{x}, \boldsymbol{y})=p(\boldsymbol{x}) p(\boldsymbol{y}) .$$

직관적으로, 두 확률 변수 $X$와 $Y$는 $\boldsymbol{y}$의 값이 (일단 알려지면) $\boldsymbol{x}$에 대한 추가 정보를 제공하지 않을 때 (그리고 그 반대도 마찬가지) 독립이다. 만약 $X, Y$가 (통계적으로) 독립이라면, 다음이 성립한다.

• $p(\boldsymbol{y} \mid \boldsymbol{x})=p(\boldsymbol{y})$
• $p(\boldsymbol{x} \mid \boldsymbol{y})=p(\boldsymbol{x})$
• $\mathbb{V}_{X, Y}[\boldsymbol{x}+\boldsymbol{y}]=\mathbb{V}_{X}[\boldsymbol{x}]+\mathbb{V}_{Y}[\boldsymbol{y}]$
• $\operatorname{Cov}_{X, Y}[\boldsymbol{x}, \boldsymbol{y}]=\mathbf{0}$

마지막 항목은 역으로 성립하지 않을 수 있다. 즉, 두 확률 변수는 공분산이 0이지만 통계적으로 독립이 아닐 수 있다. 그 이유를 이해하려면, 공분산이 선형 의존성만을 측정한다는 점을 상기해야 한다. 따라서 비선형적으로 의존하는 확률 변수는 공분산이 0일 수 있다.

Example 6.5

평균이 0인 확률 변수 $X$ ( $\mathbb{E}_{X}[x]=0$ )와 $\mathbb{E}_{X}\left[x^{3}\right]=0$ 인 경우를 고려해 보자. $y=x^{2}$ (따라서 $Y$는 $X$에 종속적이다)라고 하고, $X$와 $Y$ 사이의 공분산 (6.36)을 고려해 보자. 하지만 이것은 다음과 같이 주어진다.

$$\operatorname{Cov}[x, y]=\mathbb{E}[x y]-\mathbb{E}[x] \mathbb{E}[y]=\mathbb{E}\left[x^{3}\right]=0$$

"Mathematics for Machine Learning" 초안 (2021-07-29). 피드백: https://mml-book.com.

머신러닝에서 우리는 종종 독립적이고 동일하게 분포된(i.i.d.) 확률 변수 $X_{1}, \ldots, X_{N}$로 모델링될 수 있는 문제들을 고려한다. 두 개 이상의 확률 변수에 대해 "독립적"이라는 단어(정의 6.10)는 일반적으로 상호 독립적인 확률 변수를 의미하며, 모든 부분집합이 독립적이다(Pollard (2002, chapter 4) 및 Jacod and Protter (2004, chapter 3) 참조). "동일하게 분포된"이라는 구문은 모든 확률 변수가 동일한 분포에서 나온다는 것을 의미한다.

머신러닝에서 중요한 또 다른 개념은 조건부 독립이다.

정의 6.11 (조건부 독립). 두 확률 변수 $X$와 $Y$는 $Z$가 주어졌을 때 조건부 독립이다. 이는 다음을 만족할 때이다.

$$p(\boldsymbol{x}, \boldsymbol{y} \mid \boldsymbol{z})=p(\boldsymbol{x} \mid \boldsymbol{z}) p(\boldsymbol{y} \mid \boldsymbol{z}) \quad \text { for all } \quad \boldsymbol{z} \in \mathcal{Z},$$

여기서 $\mathcal{Z}$는 확률 변수 $Z$의 상태 집합이다. 우리는 $X \Perp Y \mid Z$로 $X$가 $Z$가 주어졌을 때 $Y$와 조건부 독립임을 나타낸다.

정의 6.11은 (6.55)의 관계가 $\boldsymbol{z}$의 모든 값에 대해 참이어야 한다고 요구한다. (6.55)의 해석은 "$\boldsymbol{z}$에 대한 지식이 주어졌을 때, $\boldsymbol{x}$와 $\boldsymbol{y}$의 분포가 분해된다"로 이해될 수 있다. 독립성은 $X \Perp Y \mid \emptyset$로 작성하면 조건부 독립의 특수한 경우로 간주될 수 있다. 확률의 곱셈 규칙 (6.22)을 사용하여 (6.55)의 좌변을 전개하면 다음을 얻을 수 있다.

$$p(\boldsymbol{x}, \boldsymbol{y} \mid \boldsymbol{z})=p(\boldsymbol{x} \mid \boldsymbol{y}, \boldsymbol{z}) p(\boldsymbol{y} \mid \boldsymbol{z}) .$$

(6.55)의 우변과 (6.56)을 비교하면 $p(\boldsymbol{y} \mid \boldsymbol{z})$가 둘 다에 나타나므로 다음을 알 수 있다.

$$p(\boldsymbol{x} \mid \boldsymbol{y}, \boldsymbol{z})=p(\boldsymbol{x} \mid \boldsymbol{z}) .$$

방정식 (6.57)은 조건부 독립, 즉 $X \Perp Y \mid Z$의 대체 정의를 제공한다. 이 대체 표현은 "$\boldsymbol{z}$를 알고 있을 때, $\boldsymbol{y}$에 대한 지식이 $\boldsymbol{x}$에 대한 우리의 지식을 변경하지 않는다"는 해석을 제공한다.

6.4.6 Inner Products of Random Variables

섹션 3.2의 내적 정의를 상기해 보자. 우리는 확률 변수 간의 내적을 정의할 수 있으며, 이 섹션에서 간략하게 설명한다. 두 개의 상관 없는(uncorrelated) 확률 변수 $X, Y$가 있다면,

$$\mathbb{V}[x+y]=\mathbb{V}[x]+\mathbb{V}[y] .$$

분산은 제곱 단위로 측정되므로, 이는 직각삼각형의 피타고라스 정리 $c^{2}=a^{2}+b^{2}$와 매우 유사하게 보인다.

다음에서는 (6.58)의 상관 없는 확률 변수의 분산 관계에 대한 기하학적 해석을 찾을 수 있는지 살펴본다.

다변량 확률 변수 간의 내적도 유사한 방식으로 다룰 수 있다.

그림 6.6 확률 변수의 기하학. 확률 변수 $X$와 $Y$가 상관이 없다면, 이들은 해당 벡터 공간에서 **직교 벡터(orthogonal vectors)**이며, 피타고라스 정리가 적용된다.

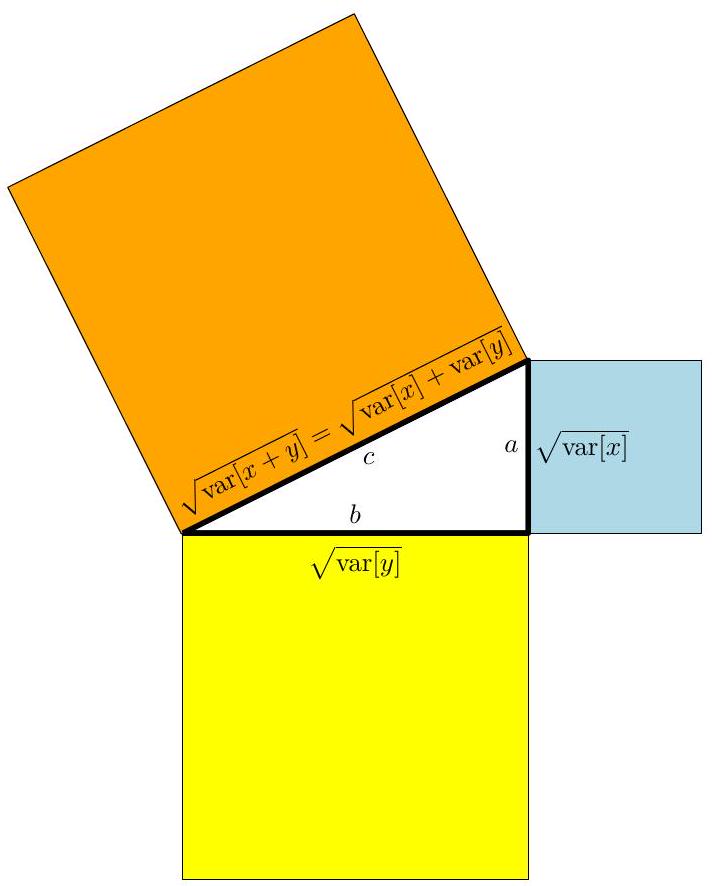
확률 변수는 벡터 공간의 벡터로 간주될 수 있으며, 우리는 확률 변수의 기하학적 속성을 얻기 위해 내적을 정의할 수 있다 (Eaton, 2007). 평균이 0인(zero mean) 확률 변수 $X$와 $Y$에 대해

$$\langle X, Y\rangle:=\operatorname{Cov}[x, y]$$

로 정의하면 내적을 얻는다. 공분산은 대칭적이고, 양의 정부호이며, 각 인수에 대해 선형임을 알 수 있다. 확률 변수의 길이는 다음과 같다.

$$\|X\|=\sqrt{\operatorname{Cov}[x, x]}=\sqrt{\mathbb{V}[x]}=\sigma[x],$$

즉, **표준 편차(standard deviation)**이다. 확률 변수가 "길수록" 불확실성이 커지며, 길이가 0인 확률 변수는 **결정론적(deterministic)**이다.

두 확률 변수 $X, Y$ 사이의 각도 $\theta$를 보면, 다음과 같다.

$$\cos \theta=\frac{\langle X, Y\rangle}{\|X\|\|Y\|}=\frac{\operatorname{Cov}[x, y]}{\sqrt{\mathbb{V}[x] \mathbb{V}[y]}},$$

이는 두 확률 변수 간의 상관 관계(correlation)(정의 6.8)이다. 이는 우리가 상관 관계를 기하학적으로 생각할 때 두 확률 변수 사이의 각도의 코사인으로 생각할 수 있음을 의미한다. 정의 3.7에서 $X \perp Y \Longleftrightarrow\langle X, Y\rangle=0$임을 알고 있다. 우리의 경우, 이는 $X$와 $Y$가 $\operatorname{Cov}[x, y]=0$인 경우에만 직교한다는 것을 의미하며, 즉 **상관이 없다(uncorrelated)**는 것이다. 그림 6.6은 이 관계를 보여준다. 비고. 유클리드 거리(이전 내적 정의로부터 구성됨)를 사용하여 확률 분포를 비교하는 것은 매력적이지만, 불행히도 분포 간의 거리를 얻는 가장 좋은 방법은 아니다. 확률 질량(또는 밀도)은 양수이며 합이 1이 되어야 함을 상기하라. 이러한 제약 조건은 분포가 **통계적 다양체(statistical manifold)**라고 불리는 공간에 존재한다는 것을 의미한다. 이 확률 분포 공간에 대한 연구를 **정보 기하학(information geometry)**이라고 한다. 분포 간의 거리를 계산하는 것은 종종 Kullback-Leibler divergence를 사용하여 수행되는데, 이는 통계적 다양체의 속성을 설명하는 거리의 일반화이다. 유클리드 거리가 metric(섹션 3.3)의 특수한 경우인 것처럼, Kullback-Leibler divergence는 Bregman divergences와 f-divergences라고 불리는 두 가지 더 일반적인 divergence 클래스의 특수한 경우이다. divergence에 대한 연구는 이 책의 범위를 벗어나므로, 더 자세한 내용은 정보 기하학 분야의 창시자 중 한 명인 Amari (2016)의 최근 저서를 참조한다.

그림 6.7 두 확률 변수 $x_{1}$과 $x_{2}$의 가우시안 분포.

6.5 Gaussian Distribution

**가우시안 분포(Gaussian distribution)**는 연속형 확률 변수(continuous-valued random variables)에 대해 가장 잘 연구된 확률 분포이다. 이는 **정규 분포(normal distribution)**라고도 불린다. 그 중요성은 계산상 편리한 많은 속성을 가지고 있다는 사실에서 비롯되며, 이에 대해서는 다음에서 논의할 것이다. 특히, 우리는 이를 사용하여 선형 회귀(9장)의 **가능도(likelihood)**와 **사전 분포(prior)**를 정의하고, 밀도 추정(11장)을 위해 **가우시안 혼합(mixture of Gaussians)**을 고려할 것이다.

가우시안 분포를 활용하는 머신러닝의 다른 많은 분야로는 가우시안 프로세스(Gaussian processes), 변분 추론(variational inference), 강화 학습(reinforcement learning) 등이 있다. 또한 신호 처리(예: 칼만 필터(Kalman filter)), 제어(예: 선형 이차 조절기(linear quadratic regulator)), 통계(예: 가설 검정(hypothesis testing))와 같은 다른 응용 분야에서도 널리 사용된다.

정규 분포(normal distribution) 가우시안 분포는 독립적이고 동일하게 분포된 확률 변수(independent and identically distributed random variables)의 합을 고려할 때 자연스럽게 나타난다. 이는 **중심 극한 정리(central limit theorem)**로 알려져 있다 (Grinstead and Snell, 1997).

다변량 가우시안 분포(multivariate Gaussian distribution) 평균 벡터(mean vector) 공분산 행렬(covariance matrix)

**다변량 정규 분포(multivariate normal distribution)**라고도 알려져 있다. 표준 정규 분포(standard normal distribution)

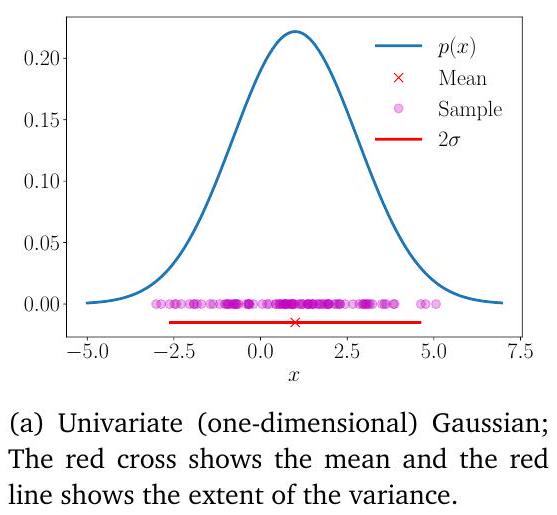
그림 6.8 100개의 샘플과 함께 오버레이된 가우시안 분포. (a) 1차원 경우; (b) 2차원 경우.

확률 및 분포

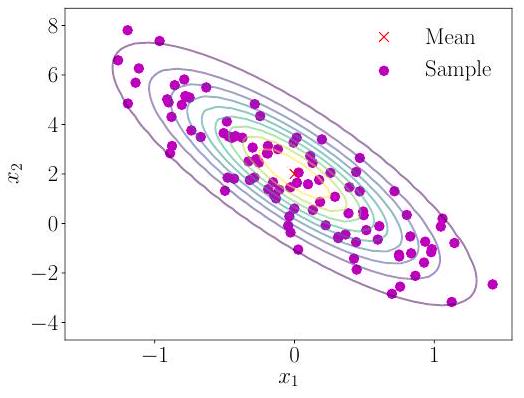
(b) 위에서 본 다변량(2차원) 가우시안. 빨간색 십자가는 평균을 나타내고, 색깔 있는 선은 밀도의 등고선을 나타낸다.

단변량 확률 변수의 경우, 가우시안 분포의 밀도는 다음과 같이 주어진다.

$$p\left(x \mid \mu, \sigma^{2}\right)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) .$$

**다변량 가우시안 분포(multivariate Gaussian distribution)**는 평균 벡터(mean vector) $\boldsymbol{\mu}$와 공분산 행렬(covariance matrix) $\boldsymbol{\Sigma}$로 완전히 특징지어지며 다음과 같이 정의된다.

$$p(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma})=(2 \pi)^{-\frac{D}{2}}|\boldsymbol{\Sigma}|^{-\frac{1}{2}} \exp \left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\top} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right),$$

여기서 $\boldsymbol{x} \in \mathbb{R}^{D}$이다. 우리는 $p(\boldsymbol{x})=\mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma})$ 또는 $X \sim \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$로 표기한다. 그림 6.7은 해당 등고선 플롯과 함께 이변량 가우시안(메쉬)을 보여준다. 그림 6.8은 해당 샘플과 함께 단변량 가우시안과 이변량 가우시안을 보여준다. 평균이 0이고 공분산이 항등 행렬인 가우시안의 특수한 경우, 즉 $\boldsymbol{\mu}=\mathbf{0}$ 및 $\boldsymbol{\Sigma}=\boldsymbol{I}$는 **표준 정규 분포(standard normal distribution)**라고 불린다.

가우시안 분포는 **주변 분포(marginal distributions)**와 **조건부 분포(conditional distributions)**에 대한 **닫힌 형식 표현(closed-form expressions)**을 가지고 있기 때문에 통계적 추정 및 머신러닝에서 널리 사용된다. 9장에서는 선형 회귀를 위해 이러한 닫힌 형식 표현을 광범위하게 사용한다. 가우시안 확률 변수로 모델링하는 주요 장점은 변수 변환(variable transformations)(6.7절)이 종종 필요하지 않다는 것이다. 가우시안 분포는 평균과 공분산에 의해 완전히 지정되므로, 우리는 종종 확률 변수의 평균과 공분산에 변환을 적용하여 변환된 분포를 얻을 수 있다.

6.5.1 Marginals and Conditionals of Gaussians are Gaussians

다음으로, 다변량 확률 변수의 일반적인 경우에 대한 marginalization과 conditioning을 제시한다. 처음 읽을 때 혼란스러울 수 있다면, 두 개의 단변량 확률 변수를 대신 고려하는 것이 좋다. $X$와 $Y$를 서로 다른 차원을 가질 수 있는 두 개의 다변량 확률 변수라고 하자. 확률의 합 규칙(sum rule)을 적용하는 효과와 conditioning의 효과를 고려하기 위해, 연결된 상태 $\left[\boldsymbol{x}^{\top}, \boldsymbol{y}^{\top}\right]$의 관점에서 Gaussian distribution을 명시적으로 작성하면 다음과 같다.

$$p(\boldsymbol{x}, \boldsymbol{y})=\mathcal{N}\left(\left[\begin{array}{l} \boldsymbol{\mu}_{x} \\ \boldsymbol{\mu}_{y} \end{array}\right],\left[\begin{array}{ll} \boldsymbol{\Sigma}_{x x} & \boldsymbol{\Sigma}_{x y} \\ \boldsymbol{\Sigma}_{y x} & \boldsymbol{\Sigma}_{y y} \end{array}\right]\right) .$$

여기서 $\boldsymbol{\Sigma}_{x x}=\operatorname{Cov}[\boldsymbol{x}, \boldsymbol{x}]$와 $\boldsymbol{\Sigma}_{y y}=\operatorname{Cov}[\boldsymbol{y}, \boldsymbol{y}]$는 각각 $\boldsymbol{x}$와 $\boldsymbol{y}$의 marginal covariance matrices이고, $\boldsymbol{\Sigma}_{x y}=\operatorname{Cov}[\boldsymbol{x}, \boldsymbol{y}]$는 $\boldsymbol{x}$와 $\boldsymbol{y}$ 사이의 cross-covariance matrix이다.

conditional distribution $p(\boldsymbol{x} \mid \boldsymbol{y})$ 또한 Gaussian이며 (그림 6.9(c)에 설명되어 있음), 다음으로 주어진다 (Bishop, 2006의 섹션 2.3에서 유도됨).

$$\begin{aligned} p(\boldsymbol{x} \mid \boldsymbol{y}) & =\mathcal{N}\left(\boldsymbol{\mu}_{x \mid y}, \boldsymbol{\Sigma}_{x \mid y}\right) \\ \boldsymbol{\mu}_{x \mid y} & =\boldsymbol{\mu}_{x}+\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1}\left(\boldsymbol{y}-\boldsymbol{\mu}_{y}\right) \\ \boldsymbol{\Sigma}_{x \mid y} & =\boldsymbol{\Sigma}_{x x}-\boldsymbol{\Sigma}_{x y} \boldsymbol{\Sigma}_{y y}^{-1} \boldsymbol{\Sigma}_{y x} \end{aligned}$$

(6.66)의 평균 계산에서 $\boldsymbol{y}$-값은 관측치이며 더 이상 무작위가 아니라는 점에 유의하라.
참고. conditional Gaussian distribution은 posterior distributions에 관심이 있는 많은 곳에서 나타난다:

• Kalman filter (Kalman, 1960)는 신호 처리에서 상태 추정을 위한 가장 핵심적인 알고리즘 중 하나로, joint distributions의 Gaussian conditionals을 계산하는 역할을 한다 (Deisenroth and Ohlsson, 2011; Särkkä, 2013).
• Gaussian processes (Rasmussen and Williams, 2006)는 함수에 대한 분포의 실용적인 구현이다. Gaussian process에서 우리는 확률 변수의 joint Gaussianity를 가정한다. 관측된 데이터에 대한 (Gaussian) conditioning을 통해 함수에 대한 posterior distribution을 결정할 수 있다.
• Latent linear Gaussian models (Roweis and Ghahramani, 1999; Murphy, 2012)에는 probabilistic principal component analysis (PPCA) (Tipping and Bishop, 1999)가 포함된다. 섹션 10.7에서 PPCA를 더 자세히 살펴볼 것이다.

joint Gaussian distribution $p(\boldsymbol{x}, \boldsymbol{y})$ (6.64)의 marginal distribution $p(\boldsymbol{x})$는 그 자체로 Gaussian이며, 합 규칙 (6.20)을 적용하여 계산되며 다음과 같이 주어진다.

$$p(\boldsymbol{x})=\int p(\boldsymbol{x}, \boldsymbol{y}) \mathrm{d} \boldsymbol{y}=\mathcal{N}\left(\boldsymbol{x} \mid \boldsymbol{\mu}_{x}, \boldsymbol{\Sigma}_{x x}\right) .$$

해당 결과는 $\boldsymbol{x}$에 대해 marginalizing하여 얻어지는 $p(\boldsymbol{y})$에도 적용된다. 직관적으로, (6.64)의 joint distribution을 보면, 우리는 관심 없는 모든 것을 무시한다 (즉, 적분하여 제거한다). 이는 그림 6.9(b)에 설명되어 있다.

Example 6.6

(a) 이변량 가우시안 (Bivariate Gaussian).

Figure 6.9 (a) 이변량 가우시안; (b) 결합 가우시안 분포의 주변 분포(marginal)는 가우시안 분포; (c) 가우시안 분포의 조건부 분포(conditional distribution) 또한 가우시안 분포.

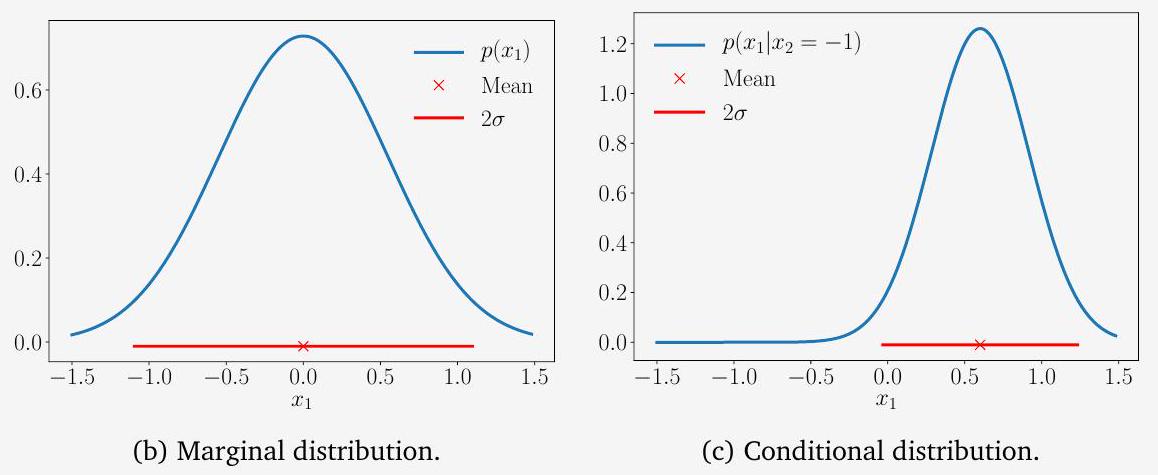
이변량 가우시안 분포(Figure 6.9 참조)를 고려해 보자:

$$p\left(x_{1}, x_{2}\right)=\mathcal{N}\left(\left[\begin{array}{l} 0 \\ 2 \end{array}\right],\left[\begin{array}{cc} 0.3 & -1 \\ -1 & 5 \end{array}\right]\right) .$$

$x_{2}=-1$로 조건화된 단변량 가우시안의 파라미터는 (6.66)과 (6.67)을 적용하여 각각 평균과 분산을 얻을 수 있다. 수치적으로는 다음과 같다:

$$\mu_{x_{1} \mid x_{2}=-1}=0+(-1) \cdot 0.2 \cdot(-1-2)=0.6$$

그리고

$$\sigma_{x_{1} \mid x_{2}=-1}^{2}=0.3-(-1) \cdot 0.2 \cdot(-1)=0.1 .$$

따라서 조건부 가우시안은 다음과 같이 주어진다:

$$p\left(x_{1} \mid x_{2}=-1\right)=\mathcal{N}(0.6,0.1) .$$

반면, 주변 분포(marginal distribution) $p\left(x_{1}\right)$는 (6.68)을 적용하여 얻을 수 있으며, 이는 본질적으로 확률 변수 $x_{1}$의 평균과 분산을 사용하여 다음과 같이 나타낸다:

$$p\left(x_{1}\right)=\mathcal{N}(0,0.3) .$$

6.5.2 Product of Gaussian Densities

선형 회귀(9장)의 경우, Gaussian likelihood를 계산해야 한다. 또한, Gaussian prior(9.3절)를 가정할 수도 있다. 우리는 Bayes' Theorem을 적용하여 posterior를 계산하는데, 이는 likelihood와 prior의 곱, 즉 두 Gaussian density의 곱으로 이어진다. 두 Gaussian $\mathcal{N}(\boldsymbol{x} \mid \boldsymbol{a}, \boldsymbol{A}) \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{b}, \boldsymbol{B})$의 곱은 $c \in \mathbb{R}$로 스케일링된 Gaussian distribution이며, $c \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{c}, \boldsymbol{C})$로 주어진다. 여기서

$$\begin{aligned} \boldsymbol{C} & =\left(\boldsymbol{A}^{-1}+\boldsymbol{B}^{-1}\right)^{-1} \\ \boldsymbol{c} & =\boldsymbol{C}\left(\boldsymbol{A}^{-1} \boldsymbol{a}+\boldsymbol{B}^{-1} \boldsymbol{b}\right) \\ c & =(2 \pi)^{-\frac{D}{2}}|\boldsymbol{A}+\boldsymbol{B}|^{-\frac{1}{2}} \exp \left(-\frac{1}{2}(\boldsymbol{a}-\boldsymbol{b})^{\top}(\boldsymbol{A}+\boldsymbol{B})^{-1}(\boldsymbol{a}-\boldsymbol{b})\right) . \end{aligned}$$

스케일링 상수 $c$ 자체는 "확장된" covariance matrix $\boldsymbol{A}+\boldsymbol{B}$를 사용하여 $\boldsymbol{a}$ 또는 $\boldsymbol{b}$에 대한 Gaussian density 형태로 작성될 수 있다. 즉, $c=\mathcal{N}(\boldsymbol{a} \mid \boldsymbol{b}, \boldsymbol{A}+\boldsymbol{B})=\mathcal{N}(\boldsymbol{b} \mid \boldsymbol{a}, \boldsymbol{A}+\boldsymbol{B})$이다.
참고. 표기상의 편의를 위해, $\boldsymbol{x}$가 random variable이 아니더라도 Gaussian density의 함수 형태를 설명하기 위해 $\mathcal{N}(\boldsymbol{x} \mid \boldsymbol{m}, \boldsymbol{S})$를 사용할 때가 있다. 우리는 앞선 설명에서 다음과 같이 작성했을 때 방금 그렇게 했다.

$$c=\mathcal{N}(\boldsymbol{a} \mid \boldsymbol{b}, \boldsymbol{A}+\boldsymbol{B})=\mathcal{N}(\boldsymbol{b} \mid \boldsymbol{a}, \boldsymbol{A}+\boldsymbol{B}) .$$

여기서 $\boldsymbol{a}$나 $\boldsymbol{b}$는 random variable이 아니다. 그러나 $c$를 이런 식으로 작성하는 것이 (6.76)보다 더 간결하다. $\square$

6.5.3 Sums and Linear Transformations

만약 $X, Y$가 독립적인 가우시안 확률 변수(즉, 결합 분포가 $p(\boldsymbol{x}, \boldsymbol{y})=p(\boldsymbol{x}) p(\boldsymbol{y})$로 주어짐)이고, $p(\boldsymbol{x})=\mathcal{N}\left(\boldsymbol{x} \mid \boldsymbol{\mu}_{x}, \boldsymbol{\Sigma}_{x}\right)$ 및 $p(\boldsymbol{y})=\mathcal{N}\left(\boldsymbol{y} \mid \boldsymbol{\mu}_{y}, \boldsymbol{\Sigma}_{y}\right)$라면, $\boldsymbol{x}+\boldsymbol{y}$ 또한 가우시안 분포를 따르며 다음과 같이 주어진다:

$$p(\boldsymbol{x}+\boldsymbol{y})=\mathcal{N}\left(\boldsymbol{\mu}_{x}+\boldsymbol{\mu}_{y}, \boldsymbol{\Sigma}_{x}+\boldsymbol{\Sigma}_{y}\right) .$$

$p(\boldsymbol{x}+\boldsymbol{y})$가 가우시안 분포를 따른다는 것을 알면, 평균과 공분산 행렬은 (6.46)부터 (6.49)까지의 결과를 사용하여 즉시 결정될 수 있다. 이 속성은 선형 회귀(9장)의 경우처럼 확률 변수에 작용하는 i.i.d. Gaussian noise를 고려할 때 중요하게 활용될 것이다.

Example 6.7

기댓값은 선형 연산이므로, 독립적인 가우시안 확률 변수들의 가중합을 다음과 같이 얻을 수 있다.

$$p(a \boldsymbol{x}+b \boldsymbol{y})=\mathcal{N}\left(a \boldsymbol{\mu}_{x}+b \boldsymbol{\mu}_{y}, a^{2} \boldsymbol{\Sigma}_{x}+b^{2} \boldsymbol{\Sigma}_{y}\right) .$$

이 유도는 이 장의 마지막에 있는 연습 문제이다.

참고. 11장에서 유용하게 사용될 경우는 가우시안 밀도의 가중합이다. 이는 가우시안 확률 변수의 가중합과는 다르다.

정리 6.12에서 확률 변수 $x$는 두 밀도 $p_{1}(x)$와 $p_{2}(x)$의 혼합 밀도에서 추출되며, $\alpha$에 의해 가중된다. 기댓값의 선형성은 다변량 확률 변수에도 적용되므로, 이 정리는 다변량 확률 변수 사례로 일반화될 수 있다. 그러나 제곱된 확률 변수의 개념은 $\boldsymbol{x} \boldsymbol{x}^{\top}$로 대체되어야 한다.

정리 6.12. 두 단변량 가우시안 밀도의 혼합을 고려하자.

$$p(x)=\alpha p_{1}(x)+(1-\alpha) p_{2}(x)$$

여기서 스칼라 $0<\alpha<1$는 혼합 가중치이며, $p_{1}(x)$와 $p_{2}(x)$는 서로 다른 매개변수, 즉 $\left(\mu_{1}, \sigma_{1}^{2}\right) \neq\left(\mu_{2}, \sigma_{2}^{2}\right)$를 갖는 단변량 가우시안 밀도(식 (6.62))이다.

그러면 혼합 밀도 $p(x)$의 평균은 각 확률 변수의 평균의 가중합으로 주어진다.

$$\mathbb{E}[x]=\alpha \mu_{1}+(1-\alpha) \mu_{2}$$

혼합 밀도 $p(x)$의 분산은 다음과 같이 주어진다. $\mathbb{V}[x]=\left[\alpha \sigma_{1}^{2}+(1-\alpha) \sigma_{2}^{2}\right]+\left(\left[\alpha \mu_{1}^{2}+(1-\alpha) \mu_{2}^{2}\right]-\left[\alpha \mu_{1}+(1-\alpha) \mu_{2}\right]^{2}\right)$.

증명. 혼합 밀도 $p(x)$의 평균은 각 확률 변수의 평균의 가중합으로 주어진다. 우리는 평균의 정의(정의 6.4)를 적용하고, 혼합식 (6.80)을 대입하면 다음과 같다.

$$\begin{aligned} \mathbb{E}[x] & =\int_{-\infty}^{\infty} x p(x) \mathrm{d} x \\ & =\int_{-\infty}^{\infty}\left(\alpha x p_{1}(x)+(1-\alpha) x p_{2}(x)\right) \mathrm{d} x \\ & =\alpha \int_{-\infty}^{\infty} x p_{1}(x) \mathrm{d} x+(1-\alpha) \int_{-\infty}^{\infty} x p_{2}(x) \mathrm{d} x \\ & =\alpha \mu_{1}+(1-\alpha) \mu_{2} \end{aligned}$$

분산을 계산하기 위해, 우리는 (6.44)의 raw-score version of the variance를 사용할 수 있으며, 이는 제곱된 확률 변수의 기댓값에 대한 표현을 필요로 한다. 여기서 우리는 확률 변수의 함수(제곱)의 기댓값 정의(정의 6.3)를 사용한다.

$$\begin{aligned} \mathbb{E}\left[x^{2}\right] & =\int_{-\infty}^{\infty} x^{2} p(x) \mathrm{d} x \\ & =\int_{-\infty}^{\infty}\left(\alpha x^{2} p_{1}(x)+(1-\alpha) x^{2} p_{2}(x)\right) \mathrm{d} x \end{aligned}$$ $$\begin{aligned} & =\alpha \int_{-\infty}^{\infty} x^{2} p_{1}(x) \mathrm{d} x+(1-\alpha) \int_{-\infty}^{\infty} x^{2} p_{2}(x) \mathrm{d} x \\ & =\alpha\left(\mu_{1}^{2}+\sigma_{1}^{2}\right)+(1-\alpha)\left(\mu_{2}^{2}+\sigma_{2}^{2}\right) \end{aligned}$$

마지막 등식에서 우리는 다시 분산의 raw-score version (6.44)인 $\sigma^{2}=\mathbb{E}\left[x^{2}\right]-\mu^{2}$를 사용했다. 이는 제곱된 확률 변수의 기댓값이 제곱된 평균과 분산의 합이 되도록 재배열된다.

따라서 분산은 (6.83d)를 (6.84d)에서 빼서 주어진다.

\begin{aligned} \mathbb{V}[x]= & \mathbb{E}\left[x^{2}\right]-(\mathbb{E}[x])^{2} \\ = & \alpha\left(\mu_{1}^{2}+\sigma_{1}^{2}\right)+(1-\alpha)\left(\mu_{2}^{2}+\sigma_{2}^{2}\right)-\left(\alpha \mu_{1}+(1-\alpha) \mu_{2}\right)^{2} \\ = & {\left[\alpha \sigma_{1}^{2}+(1-\alpha) \sigma_{2}^{2}\right] } \\ & +\left(\left[\alpha \mu_{1}^{2}+(1-\alpha) \mu_{2}^{2}\right]-\left[\alpha \mu_{1}+(1-\alpha) \mu_{2}\right]^{2}\right) . \end{aligned} $$ $\square$ 참고. 앞선 유도는 모든 밀도에 대해 유효하지만, 가우시안은 평균과 분산에 의해 완전히 결정되므로, 혼합 밀도는 **closed form**으로 결정될 수 있다. $\square$ 혼합 밀도의 경우, 개별 구성 요소는 조건부 분포(구성 요소 식별에 따라 조건화됨)로 간주될 수 있다. 식 (6.85c)는 **조건부 분산 공식**의 예시이며, **전체 분산의 법칙(law of total variance)**으로도 알려져 있다. 이는 일반적으로 두 확률 변수 $X$와 $Y$에 대해 $\mathbb{V}_{X}[x]=\mathbb{E}_{Y}\left[\mathbb{V}_{X}[x \mid y]\right]+\mathbb{V}_{Y}\left[\mathbb{E}_{X}[x \mid y]\right]$가 성립한다는 것을 의미한다. 즉, $X$의 (총) 분산은 **기댓값 조건부 분산**에 **조건부 평균의 분산**을 더한 값이다. 예제 6.17에서 우리는 이변량 표준 가우시안 확률 변수 $X$를 고려하고 이에 선형 변환 $\boldsymbol{A} \boldsymbol{x}$를 수행했다. 그 결과는 평균이 0이고 공분산이 $\boldsymbol{A} \boldsymbol{A}^{\top}$인 가우시안 확률 변수이다. 상수 벡터를 더하면 분포의 평균은 변하지만 분산에는 영향을 미치지 않는다는 점을 관찰하자. 즉, 확률 변수 $\boldsymbol{x}+\boldsymbol{\mu}$는 평균이 $\boldsymbol{\mu}$이고 단위 공분산을 갖는 가우시안이다. 따라서 **가우시안 확률 변수의 모든 선형/아핀 변환은 가우시안 분포를 따른다.** 가우시안 분포를 따르는 확률 변수 $X \sim \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$를 고려하자. 적절한 형태의 주어진 행렬 $\boldsymbol{A}$에 대해, $\boldsymbol{y}=\boldsymbol{A} \boldsymbol{x}$가 $\boldsymbol{x}$의 변환된 버전인 확률 변수 $Y$를 가정하자. 기댓값이 선형 연산자(6.50)임을 이용하여 $\boldsymbol{y}$의 평균을 다음과 같이 계산할 수 있다.

\mathbb{E}[\boldsymbol{y}]=\mathbb{E}[\boldsymbol{A} \boldsymbol{x}]=\boldsymbol{A} \mathbb{E}[\boldsymbol{x}]=\boldsymbol{A} \boldsymbol{\mu}

마찬가지로 $\boldsymbol{y}$의 분산은 (6.51)을 사용하여 찾을 수 있다.

\mathbb{V}[\boldsymbol{y}]=\mathbb{V}[\boldsymbol{A} \boldsymbol{x}]=\boldsymbol{A} \mathbb{V}[\boldsymbol{x}] \boldsymbol{A}^{\top}=\boldsymbol{A} \boldsymbol{\Sigma} \boldsymbol{A}^{\top}

이는 확률 변수 $\boldsymbol{y}$가 다음과 같이 분포된다는 것을 의미한다.

p(\boldsymbol{y})=\mathcal{N}\left(\boldsymbol{y} \mid \boldsymbol{A} \boldsymbol{\mu}, \boldsymbol{A} \boldsymbol{\Sigma} \boldsymbol{A}^{\top}\right) .

**전체 분산의 법칙** **가우시안 확률 변수의 모든 선형/아핀 변환은 또한 가우시안 분포를 따른다.** 이제 역변환을 고려해 보자. 즉, 확률 변수의 평균이 다른 확률 변수의 선형 변환이라는 것을 알 때이다. $M \geqslant N$인 주어진 **full rank** 행렬 $\boldsymbol{A} \in \mathbb{R}^{M \times N}$에 대해, $\boldsymbol{y} \in \mathbb{R}^{M}$가 평균이 $\boldsymbol{A} \boldsymbol{x}$인 가우시안 확률 변수라고 하자. 즉,

p(\boldsymbol{y})=\mathcal{N}(\boldsymbol{y} \mid \boldsymbol{A} \boldsymbol{x}, \boldsymbol{\Sigma}) .

해당 확률 분포 $p(\boldsymbol{x})$는 무엇인가? 만약 $\boldsymbol{A}$가 **invertible**하다면, 우리는 $\boldsymbol{x}=\boldsymbol{A}^{-1} \boldsymbol{y}$라고 쓰고 이전 단락의 변환을 적용할 수 있다. 그러나 일반적으로 $\boldsymbol{A}$는 **invertible**하지 않으며, 우리는 **pseudo-inverse** (3.57)와 유사한 접근 방식을 사용한다. 즉, 양변에 $\boldsymbol{A}^{\top}$를 **premultiply**한 다음, 대칭적이고 **positive definite**인 $\boldsymbol{A}^{\top} \boldsymbol{A}$를 **invert**하여 다음과 같은 관계를 얻는다.

\boldsymbol{y}=\boldsymbol{A} \boldsymbol{x} \Longleftrightarrow\left(\boldsymbol{A}^{\top} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\top} \boldsymbol{y}=\boldsymbol{x} .

따라서 $\boldsymbol{x}$는 $\boldsymbol{y}$의 선형 변환이며, 우리는 다음을 얻는다.

p(\boldsymbol{x})=\mathcal{N}\left(\boldsymbol{x} \mid\left(\boldsymbol{A}^{\top} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\top} \boldsymbol{y},\left(\boldsymbol{A}^{\top} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\top} \boldsymbol{\Sigma} \boldsymbol{A}\left(\boldsymbol{A}^{\top} \boldsymbol{A}\right)^{-1}\right) .

### 6.5.4 Sampling from Multivariate Gaussian Distributions 컴퓨터에서의 무작위 샘플링의 미묘한 점은 설명하지 않을 것이며, 관심 있는 독자는 Gentle (2004)를 참조하기 바란다. 다변수 Gaussian의 경우, 이 과정은 세 단계로 구성된다: 첫째, 구간 $[0,1]$에서 균일한 샘플을 제공하는 **의사 난수(pseudo-random numbers)**의 소스가 필요하다; 둘째, Box-Müller 변환(Devroye, 1986)과 같은 비선형 변환을 사용하여 단변수 Gaussian에서 샘플을 얻는다; 셋째, 이 샘플들의 벡터를 취합하여 다변수 표준 정규 분포 $\mathcal{N}(\mathbf{0}, \boldsymbol{I})$에서 샘플을 얻는다. 일반적인 다변수 Gaussian, 즉 평균이 0이 아니고 공분산이 단위 행렬이 아닌 경우, 우리는 Gaussian 확률 변수의 선형 변환 속성을 사용한다. 평균 $\boldsymbol{\mu}$와 공분산 행렬 $\boldsymbol{\Sigma}$를 갖는 다변수 Gaussian 분포에서 $i=1, \ldots, n$인 샘플 $\boldsymbol{x}_{i}$를 생성하는 데 관심이 있다고 가정하자. 행렬의 Cholesky factorization을 계산하려면 행렬이 대칭이고 양의 정부호(positive definite)여야 한다(섹션 3.2.3). 공분산 행렬은 이 속성을 가지고 있다. 우리는 다변수 표준 정규 분포 $\mathcal{N}(\mathbf{0}, \boldsymbol{I})$에서 샘플을 제공하는 샘플러로부터 샘플을 구성하고자 한다. 다변수 정규 분포 $\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$에서 샘플을 얻기 위해, 우리는 Gaussian 확률 변수의 선형 변환 속성을 사용할 수 있다: 만약 $\boldsymbol{x} \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I})$이면, $\boldsymbol{y}=\boldsymbol{A} \boldsymbol{x}+\boldsymbol{\mu}$는 평균 $\boldsymbol{\mu}$와 공분산 행렬 $\boldsymbol{\Sigma}$를 갖는 Gaussian 분포를 따르며, 여기서 $\boldsymbol{A} \boldsymbol{A}^{\top}=\boldsymbol{\Sigma}$이다. $\boldsymbol{A}$의 편리한 선택 중 하나는 공분산 행렬 $\boldsymbol{\Sigma}=\boldsymbol{A} \boldsymbol{A}^{\top}$의 **Cholesky decomposition** (섹션 4.3)을 사용하는 것이다. Cholesky decomposition은 $\boldsymbol{A}$가 삼각 행렬이므로 효율적인 계산을 가능하게 하는 이점이 있다. ### 6.6 Conjugacy and the Exponential Family 통계 교과서에서 볼 수 있는 "이름 있는" 확률 분포 중 상당수는 특정 유형의 현상을 모델링하기 위해 발견되었다. 예를 들어, 우리는 섹션 6.5에서 **가우시안 분포**를 살펴보았다. 이러한 분포들은 또한 복잡한 방식으로 서로 관련되어 있다 (Leemis and McQueston, 2008). 이 분야의 초보자에게는 어떤 분포를 사용해야 할지 파악하는 것이 어려울 수 있다. 또한, 이러한 분포 중 상당수는 통계와 계산이 연필과 종이로 이루어지던 시대에 발견되었다. 컴퓨팅 시대에 의미 있는 개념이 무엇인지 묻는 것은 당연하다 (Efron and Hastie, 2016). 이전 섹션에서 우리는 분포가 가우시안일 때 추론에 필요한 많은 연산이 편리하게 계산될 수 있음을 보았다. 이 시점에서 머신러닝 맥락에서 확률 분포를 조작하기 위한 **바람직한 특성(desiderata)**을 다시 상기할 필요가 있다: 1. **확률 규칙(예: 베이즈 정리)을 적용할 때 어떤 "닫힘 속성(closure property)"이 존재**해야 한다. 닫힘 속성이란 특정 연산을 적용했을 때 같은 유형의 객체를 반환하는 것을 의미한다. 2. 더 많은 데이터를 수집하더라도 분포를 설명하기 위해 더 많은 **매개변수가 필요하지 않아야** 한다. 3. 데이터로부터 학습하는 데 관심이 있으므로, **매개변수 추정(parameter estimation)이 잘 작동**하기를 원한다. **지수족(exponential family)**이라고 불리는 분포 클래스는 유리한 계산 및 추론 속성을 유지하면서도 적절한 일반성(generality)의 균형을 제공하는 것으로 밝혀졌다. 지수족을 소개하기 전에, "이름 있는" 확률 분포의 세 가지 구성원인 **베르누이(Bernoulli) 분포 (예제 6.8), 이항(Binomial) 분포 (예제 6.9), 베타(Beta) 분포 (예제 6.10)**를 살펴보자. ## Example 6.8 **베르누이 분포(Bernoulli distribution)**는 상태 $x \in\{0,1\}$를 갖는 단일 이진 확률 변수 $X$에 대한 분포이다. 이 분포는 $X=1$일 확률을 나타내는 단일 연속 매개변수 $\mu \in[0,1]$에 의해 결정된다. 베르누이 분포 $\operatorname{Ber}(\mu)$는 다음과 같이 정의된다.

\begin{aligned} p(x \mid \mu) & =\mu^{x}(1-\mu)^{1-x}, \quad x \in{0,1} \ \mathbb{E}[x] & =\mu \ \mathbb{V}[x] & =\mu(1-\mu) \end{aligned}

여기서 $\mathbb{E}[x]$와 $\mathbb{V}[x]$는 이진 확률 변수 $X$의 평균과 분산이다. 베르누이 분포가 사용될 수 있는 예시는 동전을 던질 때 "앞면"이 나올 확률을 모델링하는 경우이다. "Computers"는 과거에는 직업 설명이었다. **지수족(exponential family)** **베르누이 분포(Bernoulli distribution)** 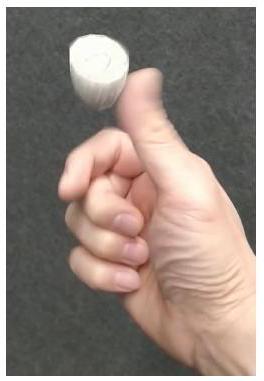 **이항 분포(Binomial distribution)** Figure 6.10 $\mu \in\{0.1,0.4,0.75\}$ 및 $N=15$일 때 이항 분포의 예시. 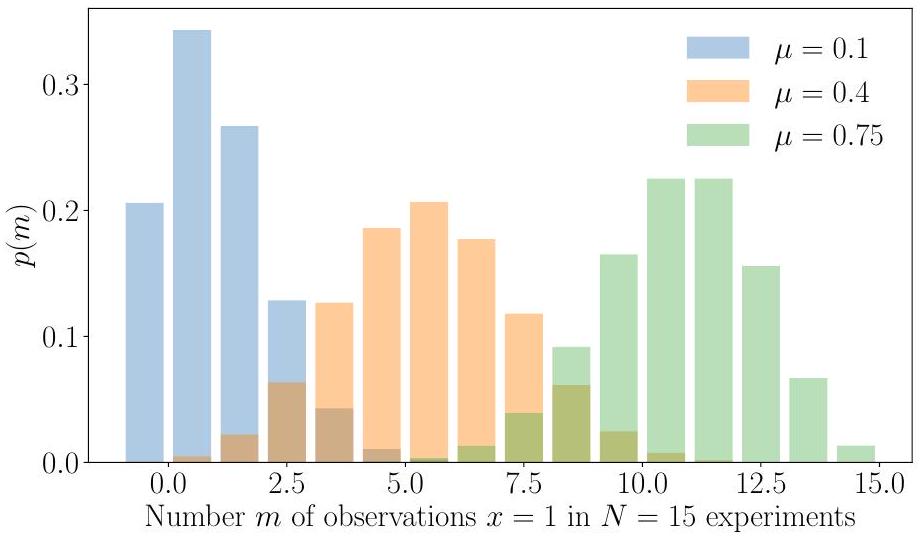 참고. 위에서 베르누이 분포를 다시 작성할 때, 부울 변수를 숫자 0 또는 1로 사용하고 이를 지수에 표현하는 방식은 머신러닝 교과서에서 자주 사용되는 기법이다. 이러한 방식은 **다항 분포(Multinomial distribution)**를 표현할 때도 나타난다. ## Example 6.9 (Binomial Distribution) **이항 분포(Binomial distribution)**는 베르누이 분포(Bernoulli distribution)를 정수(integer)에 대한 분포로 일반화한 것이다(그림 6.10 참조). 특히, 이항 분포는 $p(X=1)=\mu \in[0,1]$인 베르누이 분포에서 추출한 $N$개의 샘플 중 $X=1$이 $m$번 관측될 확률을 설명하는 데 사용될 수 있다. 이항 분포 $\operatorname{Bin}(N, \mu)$는 다음과 같이 정의된다.

\begin{aligned} p(m \mid N, \mu) & =\binom{N}{m} \mu^{m}(1-\mu)^{N-m}, \ \mathbb{E}[m] & =N \mu, \ \mathbb{V}[m] & =N \mu(1-\mu), \end{aligned}

여기서 $\mathbb{E}[m]$과 $\mathbb{V}[m]$은 각각 $m$의 평균(mean)과 분산(variance)이다. 이항 분포가 사용될 수 있는 예시로는, 단일 실험에서 앞면이 나올 확률이 $\mu$일 때, $N$번의 동전 던지기 실험에서 $m$번의 "앞면"이 관측될 확률을 설명하고자 하는 경우를 들 수 있다. ## Example 6.10 (Beta Distribution) 유한 구간에서 연속 확률 변수를 모델링해야 할 수도 있다. **Beta 분포**는 연속 확률 변수 $\mu \in[0,1]$에 대한 분포이며, 종종 어떤 이진 이벤트(예: Bernoulli 분포를 지배하는 매개변수)의 확률을 나타내는 데 사용된다. Beta 분포 $\operatorname{Beta}(\alpha, \beta)$ (그림 6.11 참조) 자체는 두 개의 매개변수 $\alpha>0, \beta>0$에 의해 결정되며 다음과 같이 정의된다.

\begin{aligned} p(\mu \mid \alpha, \beta) & =\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} \mu^{\alpha-1}(1-\mu)^{\beta-1} \ \mathbb{E}[\mu] & =\frac{\alpha}{\alpha+\beta}, \quad \mathbb{V}[\mu]=\frac{\alpha \beta}{(\alpha+\beta)^{2}(\alpha+\beta+1)} \end{aligned}

여기서 $\Gamma(\cdot)$는 다음과 같이 정의되는 Gamma 함수이다.

\begin{aligned} \Gamma(t) & :=\int_{0}^{\infty} x^{t-1} \exp (-x) d x, \quad t>0 \ \Gamma(t+1) & =t \Gamma(t) \end{aligned}

(6.98)의 Gamma 함수 비율은 Beta 분포를 정규화한다.  그림 6.11 $\alpha$와 $\beta$의 다른 값에 대한 Beta 분포의 예시. 직관적으로, $\alpha$는 확률 질량을 1쪽으로 이동시키는 반면, $\beta$는 확률 질량을 0쪽으로 이동시킨다. 몇 가지 특별한 경우가 있다 (Murphy, 2012): * $\alpha=1=\beta$인 경우, 균등 분포 $\mathcal{U}[0,1]$를 얻는다. * $\alpha, \beta<1$인 경우, 0과 1에 spike가 있는 **bimodal 분포**를 얻는다. * $\alpha, \beta>1$인 경우, 분포는 **unimodal**이다. * $\alpha, \beta>1$이고 $\alpha=\beta$인 경우, 분포는 unimodal, 대칭이며 구간 $[0,1]$의 중앙에 위치한다. 즉, mode/mean은 $\frac{1}{2}$이다. 참고. 이름이 붙은 분포들은 매우 다양하며, 서로 다른 방식으로 관련되어 있다 (Leemis and McQueston, 2008). 각 이름 붙은 분포는 특정 이유로 생성되었지만, 다른 응용 분야를 가질 수 있다는 점을 염두에 두는 것이 중요하다. 특정 분포가 생성된 이유를 아는 것은 해당 분포를 가장 잘 사용하는 방법에 대한 통찰력을 제공하는 경우가 많다. 우리는 **conjugacy** (섹션 6.6.1) 및 **exponential families** (섹션 6.6.3)의 개념을 설명하기 위해 앞서 언급한 세 가지 분포를 **conjugate prior**로 소개했다. ### 6.6.1 Conjugacy 베이즈 정리(6.23)에 따르면, **사후 분포(posterior)**는 **사전 분포(prior)**와 **가능도(likelihood)**의 곱에 비례한다. 사전 분포의 명세는 두 가지 이유로 까다로울 수 있다. 첫째, 사전 분포는 데이터를 보기 전에 문제에 대한 우리의 지식을 캡슐화해야 한다. 이는 종종 설명하기 어렵다. 둘째, 사후 분포를 분석적으로 계산하는 것이 종종 불가능하다. 그러나 계산상 편리한 몇 가지 사전 분포가 있는데, 이를 **켤레 사전 분포(conjugate priors)**라고 한다. 정의 6.13 (켤레 사전 분포). 사전 분포가 사후 분포와 동일한 형태/유형을 가질 때, 해당 사전 분포는 가능도 함수에 대한 켤레 사전 분포이다. 켤레성은 사전 분포의 매개변수를 업데이트하여 사후 분포를 대수적으로 계산할 수 있기 때문에 특히 편리하다. 참고. 확률 분포의 기하학을 고려할 때, 켤레 사전 분포는 가능도와 동일한 거리 구조를 유지한다 (Agarwal and Daumé III, 2010). 켤레 사전 분포의 구체적인 예를 소개하기 위해, 예제 6.11에서 **이항 분포(Binomial distribution)**(이산 확률 변수에 정의됨)와 **베타 분포(Beta distribution)**(연속 확률 변수에 정의됨)를 설명한다. ## Example 6.11 (Beta-Binomial Conjugacy) **이항(Binomial) 확률 변수** $x \sim \operatorname{Bin}(N, \mu)$를 고려해 보자. 여기서

p(x \mid N, \mu)=\binom{N}{x} \mu^{x}(1-\mu)^{N-x}, \quad x=0,1, \ldots, N,

는 $N$번의 동전 던지기에서 "앞면"이 $x$번 나올 확률이며, $\mu$는 "앞면"이 나올 확률이다. 우리는 모수 $\mu$에 **베타 사전 분포(Beta prior)**를 부여한다. 즉, $\mu \sim \operatorname{Beta}(\alpha, \beta)$이며, 여기서

p(\mu \mid \alpha, \beta)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} \mu^{\alpha-1}(1-\mu)^{\beta-1} .

이제 $x=h$라는 어떤 결과를 관찰했다고 가정해 보자. 즉, $N$번의 동전 던지기에서 $h$번의 앞면을 보았을 때, $\mu$에 대한 **사후 분포(posterior distribution)**를 다음과 같이 계산한다.

\begin{aligned} p(\mu \mid x=h, N, \alpha, \beta) & \propto p(x \mid N, \mu) p(\mu \mid \alpha, \beta) \ & \propto \mu^{h}(1-\mu)^{(N-h)} \mu^{\alpha-1}(1-\mu)^{\beta-1} \ & =\mu^{h+\alpha-1}(1-\mu)^{(N-h)+\beta-1} \end{aligned}

$$| Likelihood | Conjugate prior | Posterior | | :--- | :--- | :--- | | Bernoulli | Beta | Beta | | Binomial | Beta | Beta | | Gaussian | Gaussian/inverse Gamma | Gaussian/inverse Gamma | | Gaussian | Gaussian/inverse Wishart | Gaussian/inverse Wishart | | Multinomial | Dirichlet | Dirichlet | 표 6.2 일반적인 **가능도 함수(likelihood function)**에 대한 **켤레 사전 분포(conjugate prior)**의 예시.$$

\propto \operatorname{Beta}(h+\alpha, N-h+\beta),

즉, 사후 분포는 사전 분포와 동일하게 **베타 분포(Beta distribution)**이다. 다시 말해, **베타 사전 분포**는 **이항 가능도 함수(Binomial likelihood function)**의 모수 $\mu$에 대한 **켤레 사전 분포**이다. 다음 예시에서는 **베타-이항 켤레성(Beta-Binomial conjugacy)** 결과와 유사한 결과를 도출할 것이다. 여기서 우리는 **베타 분포**가 **베르누이 분포(Bernoulli distribution)**에 대한 **켤레 사전 분포**임을 보일 것이다. ## Example 6.12 (Beta-Bernoulli Conjugacy) $x \in\{0,1\}$가 파라미터 $\theta \in[0,1]$를 갖는 **베르누이 분포(Bernoulli distribution)**를 따른다고 하자. 즉, $p(x=1 \mid \theta)=\theta$이다. 이는 $p(x \mid \theta)=\theta^{x}(1-\theta)^{1-x}$로도 표현될 수 있다. $\theta$가 파라미터 $\alpha, \beta$를 갖는 **베타 분포(Beta distribution)**를 따른다고 하자. 즉, $p(\theta \mid \alpha, \beta) \propto \theta^{\alpha-1}(1-\theta)^{\beta-1}$이다. 베타 분포와 베르누이 분포를 곱하면 다음과 같다.

\begin{aligned} p(\theta \mid x, \alpha, \beta) & =p(x \mid \theta) p(\theta \mid \alpha, \beta) \ & \propto \theta^{x}(1-\theta)^{1-x} \theta^{\alpha-1}(1-\theta)^{\beta-1} \ & =\theta^{\alpha+x-1}(1-\theta)^{\beta+(1-x)-1} \ & \propto p(\theta \mid \alpha+x, \beta+(1-x)) \end{aligned}

마지막 줄은 파라미터 $(\alpha+x, \beta+(1-x))$를 갖는 **베타 분포**이다. 표 6.2는 확률론적 모델링에 사용되는 일부 표준 **가능도(likelihood)** 파라미터에 대한 **켤레 사전 분포(conjugate priors)**의 예시를 나열한다. **다항 분포(Multinomial)**, **역 감마 분포(inverse Gamma)**, **역 위샤트 분포(inverse Wishart)**, **디리클레 분포(Dirichlet)**와 같은 분포는 모든 통계학 교재에서 찾아볼 수 있으며, 예를 들어 Bishop (2006)에 설명되어 있다. **베타 분포**는 **이항 분포(Binomial)**와 **베르누이 가능도(Bernoulli likelihood)** 모두에서 파라미터 $\mu$에 대한 **켤레 사전 분포**이다. **가우시안 가능도 함수(Gaussian likelihood function)**의 경우, 평균에 대해 **켤레 가우시안 사전 분포(conjugate Gaussian prior)**를 사용할 수 있다. 가우시안 가능도가 표에 두 번 나타나는 이유는 **단변량(univariate)**과 **다변량(multivariate)** 경우를 구별해야 하기 때문이다. 단변량(스칼라)의 경우, **역 감마 분포**는 분산에 대한 **켤레 사전 분포**이다. 다변량의 경우, 공분산 행렬에 대한 사전 분포로 **켤레 역 위샤트 분포(conjugate inverse Wishart distribution)**를 사용한다. **디리클레 분포**는 다항 가능도 함수에 대한 **켤레 사전 분포**이다. 더 자세한 내용은 Bishop (2006)을 참조한다. **감마 사전 분포(Gamma prior)**는 단변량 가우시안 가능도에서 **정밀도(precision, 역분산)**에 대한 **켤레 사전 분포**이며, **위샤트 사전 분포(Wishart prior)**는 다변량 가우시안 가능도에서 **정밀도 행렬(precision matrix, 역공분산 행렬)**에 대한 **켤레 사전 분포**이다. ### 6.6.2 Sufficient Statistics 확률 변수의 **통계량(statistic)**은 해당 확률 변수의 결정론적 함수임을 상기하자. 예를 들어, $\boldsymbol{x}=\left[x_{1}, \ldots, x_{N}\right]^{\top}$가 단변량 가우시안 확률 변수의 벡터, 즉 $x_{n} \sim \mathcal{N}\left(\mu, \sigma^{2}\right)$일 때, 표본 평균 $\hat{\mu}=\frac{1}{N}\left(x_{1}+\cdots+x_{N}\right)$은 통계량이다. Sir Ronald Fisher는 **충분 통계량(sufficient statistics)**의 개념을 발견했다. 이는 고려 중인 분포에 해당하는 데이터로부터 추론할 수 있는 모든 가용한 정보를 포함하는 통계량이 존재한다는 아이디어이다. 다시 말해, 충분 통계량은 모집단에 대한 추론을 하는 데 필요한 모든 정보를 담고 있으며, 분포를 대표하기에 충분한 통계량이다. $\theta$로 매개변수화된 분포들의 집합에 대해, $X$를 미지의 $\theta_{0}$가 주어졌을 때 분포 $p\left(x \mid \theta_{0}\right)$를 따르는 확률 변수라고 하자. 통계량들의 벡터 $\phi(x)$는 $\theta_{0}$에 대한 모든 가능한 정보를 포함할 경우 $\theta_{0}$에 대한 **충분 통계량**이라고 불린다. "모든 가능한 정보를 포함한다"는 것을 더 형식적으로 설명하면, $\theta$가 주어졌을 때 $x$의 확률이 $\theta$에 의존하지 않는 부분과 $\phi(x)$를 통해서만 $\theta$에 의존하는 부분으로 인수분해될 수 있다는 의미이다. **Fisher-Neyman 인수분해 정리(factorization theorem)**는 이 개념을 형식화하며, 우리는 이를 증명 없이 정리 6.14로 제시한다. 정리 6.14 (Fisher-Neyman). [Lehmann and Casella (1998)의 정리 6.5] $X$가 확률 밀도 함수 $p(x \mid \theta)$를 가진다고 하자. 그러면 통계량 $\phi(x)$는 $p(x \mid \theta)$가 다음 형태로 작성될 수 있을 때 그리고 그 경우에만 $\theta$에 대해 충분하다.

p(x \mid \theta)=h(x) g_{\theta}(\phi(x)),

여기서 $h(x)$는 $\theta$에 독립적인 분포이고 $g_{\theta}$는 충분 통계량 $\phi(x)$를 통해 $\theta$에 대한 모든 의존성을 포착한다. 만약 $p(x \mid \theta)$가 $\theta$에 의존하지 않는다면, $\phi(x)$는 어떤 함수 $\phi$에 대해서도 자명하게 충분 통계량이다. 더 흥미로운 경우는 $p(x \mid \theta)$가 $x$ 자체는 아니고 $\phi(x)$에만 의존하는 경우이다. 이 경우, $\phi(x)$는 $\theta$에 대한 충분 통계량이다. 머신러닝에서는 분포에서 추출된 유한한 수의 샘플을 고려한다. 간단한 분포(예시 6.8의 Bernoulli 분포와 같은)의 경우, 분포의 매개변수를 추정하기 위해 소수의 샘플만 필요하다고 상상할 수 있다. 우리는 또한 반대 문제도 고려할 수 있다: 만약 우리가 데이터 집합(미지의 분포에서 추출된 샘플)을 가지고 있다면, 어떤 분포가 가장 잘 맞는가? 자연스럽게 던질 수 있는 질문은, 더 많은 데이터를 관찰할수록 분포를 설명하기 위해 더 많은 매개변수 $\theta$가 필요한가 하는 것이다. 일반적으로 답은 '그렇다'이며, 이는 **비모수 통계학(non-parametric statistics)**에서 연구된다 (Wasserman, 2007). 역으로, 어떤 분포 클래스가 **유한 차원 충분 통계량(finite-dimensional sufficient statistics)**을 가지는지, 즉 분포를 설명하는 데 필요한 매개변수의 수가 임의로 증가하지 않는지를 고려하는 질문이 있다. 그 답은 다음 섹션에서 설명하는 **지수족 분포(exponential family distributions)**이다. ### 6.6.3 Exponential Family 분포(이산 또는 연속 확률 변수의)를 고려할 때 가질 수 있는 추상화 수준은 세 가지가 있다. 첫 번째 수준(가장 구체적인 스펙트럼 끝)에서는 고정된 매개변수를 가진 특정 명명된 분포를 갖는다. 예를 들어, 평균이 0이고 분산이 1인 단변량 Gaussian $\mathcal{N}(0,1)$이 있다. 머신러닝에서는 종종 두 번째 추상화 수준을 사용한다. 즉, **매개변수 형식(단변량 Gaussian)을 고정하고 데이터로부터 매개변수를 추론**한다. 예를 들어, 알 수 없는 평균 $\mu$와 알 수 없는 분산 $\sigma^{2}$를 가진 단변량 Gaussian $\mathcal{N}\left(\mu, \sigma^{2}\right)$을 가정하고, **최대 우도 적합(maximum likelihood fit)을 사용하여 최적의 매개변수($\mu, \sigma^{2}$)를 결정**한다. 9장에서 선형 회귀를 고려할 때 이에 대한 예시를 볼 것이다. 세 번째 추상화 수준은 분포의 **패밀리(families of distributions)**를 고려하는 것이며, 이 책에서는 **exponential family**를 고려한다. 단변량 Gaussian은 exponential family의 한 멤버의 예시이다. 표 6.2의 모든 "명명된" 모델을 포함하여 널리 사용되는 많은 통계 모델은 exponential family의 멤버이다. 이들은 모두 하나의 개념으로 통합될 수 있다 (Brown, 1986). **Remark.** 간략한 역사적 일화: 수학 및 과학의 많은 개념과 마찬가지로, exponential family는 다른 연구자들에 의해 동시에 독립적으로 발견되었다. 1935-1936년에 태즈메이니아의 Edwin Pitman, 파리의 Georges Darmois, 뉴욕의 Bernard Koopman은 독립적으로 **exponential family가 반복적인 독립 샘플링 하에서 유한 차원 충분 통계량(finite-dimensional sufficient statistics)을 갖는 유일한 패밀리**임을 보였다 (Lehmann and Casella, 1998). **exponential family**는 $\boldsymbol{\theta} \in \mathbb{R}^{D}$로 매개변수화된 확률 분포의 패밀리이며, 그 형태는 다음과 같다.

p(\boldsymbol{x} \mid \boldsymbol{\theta})=h(\boldsymbol{x}) \exp (\langle\boldsymbol{\theta}, \boldsymbol{\phi}(\boldsymbol{x})\rangle-A(\boldsymbol{\theta})),

여기서 $\boldsymbol{\phi}(\boldsymbol{x})$는 **충분 통계량(sufficient statistics)**의 벡터이다. 일반적으로 (6.107)에서는 어떤 내적(Section 3.2)도 사용될 수 있으며, 구체적으로 여기서는 표준 **dot product**($\left(\langle\boldsymbol{\theta}, \boldsymbol{\phi}(\boldsymbol{x})\rangle=\boldsymbol{\theta}^{\top} \boldsymbol{\phi}(\boldsymbol{x})\right)$)를 사용할 것이다. exponential family의 형태는 본질적으로 Fisher-Neyman 정리(Theorem 6.14)에서 $g_{\theta}(\phi(x))$의 특정 표현이라는 점에 유의하라. 인자 $h(\boldsymbol{x})$는 충분 통계량 $\boldsymbol{\phi}(\boldsymbol{x})$ 벡터에 다른 항목($\log h(\boldsymbol{x})$)을 추가하고 해당 매개변수 $\theta_{0}=1$을 제약함으로써 dot product 항에 흡수될 수 있다. 항 $A(\boldsymbol{\theta})$는 분포가 합산되거나 1로 적분되도록 보장하는 **정규화 상수(normalization constant)**이며, **로그 분할 함수(log-partition function)**라고 불린다. 이 두 항을 무시하고 exponential family를 다음과 같은 형태의 분포로 고려함으로써 exponential family에 대한 좋은 직관적 개념을 얻을 수 있다.

p(\boldsymbol{x} \mid \boldsymbol{\theta}) \propto \exp \left(\boldsymbol{\theta}^{\top} \boldsymbol{\phi}(\boldsymbol{x})\right) .

이러한 매개변수화 형태에 대해 매개변수 $\boldsymbol{\theta}$는 **자연 매개변수(natural parameters)**라고 불린다. 언뜻 보기에 exponential family는 dot product 결과에 exponential 함수를 추가하여 변환하는 평범한 것처럼 보인다. 그러나 $\boldsymbol{\phi}(\boldsymbol{x})$에 데이터에 대한 정보를 담을 수 있다는 사실을 기반으로 편리한 모델링과 효율적인 계산을 가능하게 하는 많은 함의가 있다. ## Example 6.13 (Gaussian as Exponential Family) 단변량 가우시안 분포 $\mathcal{N}\left(\mu, \sigma^{2}\right)$를 고려해 보자. $\boldsymbol{\phi}(x)=\left[\begin{array}{c}x \\ x^{2}\end{array}\right]$라고 하면, **exponential family**의 정의에 따라 다음과 같다.

p(x \mid \boldsymbol{\theta}) \propto \exp \left(\theta_{1} x+\theta_{2} x^{2}\right) .

$$여기서$$

\boldsymbol{\theta}=\left[\frac{\mu}{\sigma^{2}},-\frac{1}{2 \sigma^{2}}\right]^{\top}

$$로 설정하고 (6.109)에 대입하면 다음과 같은 결과를 얻는다.$$

p(x \mid \boldsymbol{\theta}) \propto \exp \left(\frac{\mu x}{\sigma^{2}}-\frac{x^{2}}{2 \sigma^{2}}\right) \propto \exp \left(-\frac{1}{2 \sigma^{2}}(x-\mu)^{2}\right) .

따라서 단변량 가우시안 분포는 **sufficient statistic** $\boldsymbol{\phi}(x)=\left[\begin{array}{c}x \\ x^{2}\end{array}\right]$와 (6.110)에 주어진 **natural parameters** $\boldsymbol{\theta}$를 갖는 **exponential family**의 한 구성원이다. ## Example 6.14 (Bernoulli as Exponential Family) 예제 6.8의 **베르누이 분포(Bernoulli distribution)**를 상기해 보자.

p(x \mid \mu)=\mu^{x}(1-\mu)^{1-x}, \quad x \in{0,1} .

$$이는 **지수족(exponential family)** 형태로 다음과 같이 쓸 수 있다.$$

\begin{aligned} p(x \mid \mu) & =\exp \left[\log \left(\mu^{x}(1-\mu)^{1-x}\right)\right] \ & =\exp [x \log \mu+(1-x) \log (1-\mu)] \ & =\exp [x \log \mu-x \log (1-\mu)+\log (1-\mu)] \ & =\exp \left[x \log \frac{\mu}{1-\mu}+\log (1-\mu)\right] . \end{aligned}

$$마지막 줄 (6.113d)는 다음을 관찰함으로써 지수족 형태 (6.107)임을 알 수 있다.$$

h(x)=1

$$$$

\begin{aligned} \theta & =\log \frac{\mu}{1-\mu} \ \phi(x) & =x \ A(\theta) & =-\log (1-\mu)=\log (1+\exp (\theta)) . \end{aligned}

$\theta$와 $\mu$ 사이의 관계는 가역적이므로 다음과 같다.

\mu=\frac{1}{1+\exp (-\theta)} .

관계 (6.118)은 (6.117)의 오른쪽 등식을 얻는 데 사용된다. 비고. 원래의 베르누이 파라미터 $\mu$와 **자연 파라미터(natural parameter)** $\theta$ 사이의 관계는 **시그모이드(sigmoid)** 또는 **로지스틱 함수(logistic function)**로 알려져 있다. $\mu \in(0,1)$이지만 $\theta \in \mathbb{R}$임을 관찰하면, 시그모이드 함수는 실수 값을 $(0,1)$ 범위로 압축한다. 이 속성은 머신러닝에서 유용하게 사용되는데, 예를 들어 **로지스틱 회귀(logistic regression)** (Bishop, 2006, section 4.3.2)뿐만 아니라 신경망의 **비선형 활성화 함수(nonlinear activation functions)** (Goodfellow et al., 2016, chapter 6)로도 사용된다. 특정 분포(예: 표 6.2의 분포들)의 **켤레 분포(conjugate distribution)**의 파라미터 형태를 찾는 것은 종종 명확하지 않다. **지수족(exponential families)**은 켤레 분포 쌍을 찾는 편리한 방법을 제공한다. 확률 변수 $X$가 지수족 (6.107)의 멤버라고 가정해 보자.

p(\boldsymbol{x} \mid \boldsymbol{\theta})=h(\boldsymbol{x}) \exp (\langle\boldsymbol{\theta}, \boldsymbol{\phi}(\boldsymbol{x})\rangle-A(\boldsymbol{\theta})) .

$$지수족의 모든 멤버는 **켤레 사전 분포(conjugate prior)**를 갖는다 (Brown, 1986).$$

p(\boldsymbol{\theta} \mid \boldsymbol{\gamma})=h_{c}(\boldsymbol{\theta}) \exp \left(\left\langle\left[\begin{array}{l} \gamma_{1} \ \gamma_{2} \end{array}\right],\left[\begin{array}{c} \boldsymbol{\theta} \ -A(\boldsymbol{\theta}) \end{array}\right]\right\rangle-A_{c}(\boldsymbol{\gamma})\right),

여기서 $\boldsymbol{\gamma}=\left[\begin{array}{l}\gamma_{1} \\ \gamma_{2}\end{array}\right]$는 $\operatorname{dim}(\boldsymbol{\theta})+1$ 차원을 갖는다. 켤레 사전 분포의 **충분 통계량(sufficient statistics)**은 $\left[\begin{array}{c}\boldsymbol{\theta} \\ -A(\boldsymbol{\theta})\end{array}\right]$이다. 지수족에 대한 켤레 사전 분포의 일반적인 형태에 대한 지식을 사용함으로써, 특정 분포에 해당하는 켤레 사전 분포의 함수적 형태를 도출할 수 있다. ## Example 6.15 베르누이 분포의 **exponential family** 형태 (6.113d)를 상기해 보자.

p(x \mid \mu)=\exp \left[x \log \frac{\mu}{1-\mu}+\log (1-\mu)\right]

$$**canonical conjugate prior**는 다음과 같은 형태를 가진다.$$

p(\mu \mid \alpha, \beta)=\frac{\mu}{1-\mu} \exp \left[\alpha \log \frac{\mu}{1-\mu}+(\beta+\alpha) \log (1-\mu)-A_{c}(\gamma)\right]

여기서 우리는 $\gamma:=[\alpha, \beta+\alpha]^{\top}$와 $h_{c}(\mu):=\mu /(1-\mu)$로 정의했다. 식 (6.122)는 다음과 같이 단순화된다.

p(\mu \mid \alpha, \beta)=\exp \left[(\alpha-1) \log \mu+(\beta-1) \log (1-\mu)-A_{c}(\alpha, \beta)\right]

$$이를 **non-exponential family** 형태로 바꾸면 다음과 같다.$$

p(\mu \mid \alpha, \beta) \propto \mu^{\alpha-1}(1-\mu)^{\beta-1}

이는 **Beta 분포** (6.98)임을 알 수 있다. 예제 6.12에서는 Beta 분포가 베르누이 분포의 **conjugate prior**라고 가정하고 실제로 **conjugate prior**임을 보였다. 이 예제에서는 **exponential family** 형태의 베르누이 분포의 **canonical conjugate prior**를 살펴봄으로써 Beta 분포의 형태를 유도했다. 이전 섹션에서 언급했듯이, **exponential family**의 주요 동기는 **유한 차원 sufficient statistics**를 갖는다는 점이다. 또한, **conjugate distribution**은 작성하기 쉽고, **conjugate distribution** 역시 **exponential family**에서 파생된다. **추론(inference)** 관점에서 **최대 우도 추정(maximum likelihood estimation)**은 **sufficient statistics**의 **경험적 추정치(empirical estimates)**가 **sufficient statistics**의 **모집단 값(population values)**에 대한 **최적 추정치(optimal estimates)**이기 때문에 잘 작동한다(가우시안 분포의 평균과 공분산을 상기해 보라). **최적화(optimization)** 관점에서 **로그-우도 함수(log-likelihood function)**는 **오목(concave)**하므로 효율적인 최적화 접근 방식을 적용할 수 있다 (7장). ### 6.7 Change of Variables/Inverse Transform 알려진 분포가 매우 많다고 생각될 수 있지만, 실제로는 우리가 이름을 붙인 분포의 집합은 상당히 제한적이다. 따라서 **변환된 확률 변수가 어떻게 분포하는지 이해하는 것이 종종 유용**하다. 예를 들어, $X$가 단변량 정규 분포 $\mathcal{N}(0,1)$에 따라 분포하는 확률 변수라고 가정할 때, $X^{2}$의 분포는 무엇일까? 머신러닝에서 매우 흔한 또 다른 예시는, $X_{1}$과 $X_{2}$가 단변량 표준 정규 분포를 따른다고 할 때, $\frac{1}{2}\left(X_{1}+X_{2}\right)$의 분포는 무엇일까? $\frac{1}{2}\left(X_{1}+X_{2}\right)$의 분포를 알아내는 한 가지 방법은 $X_{1}$과 $X_{2}$의 평균과 분산을 계산한 다음 이를 결합하는 것이다. 섹션 6.4.4에서 보았듯이, 확률 변수의 **affine 변환**을 고려할 때 결과 확률 변수의 평균과 분산을 계산할 수 있다. 그러나 변환 하에서 분포의 함수적 형태를 얻지 못할 수도 있다. 더욱이, **닫힌 형태(closed-form) 표현을 쉽게 사용할 수 없는 확률 변수의 비선형 변환에 관심이 있을 수도 있다.** **참고 (표기법)**. 이 섹션에서는 확률 변수와 그들이 취하는 값에 대해 명확하게 설명할 것이다. 따라서, 확률 변수를 나타내기 위해 대문자 $X, Y$를 사용하고, 확률 변수가 취하는 목표 공간 $\mathcal{T}$의 값을 나타내기 위해 소문자 $x, y$를 사용한다는 점을 상기한다. 이산 확률 변수 $X$의 pmf는 $P(X=x)$로 명시적으로 작성할 것이다. 연속 확률 변수 $X$ (섹션 6.2.2)의 경우, pdf는 $f(x)$로, cdf는 $F_{X}(x)$로 작성된다. 우리는 확률 변수 변환의 분포를 얻기 위한 두 가지 접근 방식을 살펴볼 것이다: **누적 분포 함수(cumulative distribution function)의 정의를 사용하는 직접적인 접근 방식**과 **미적분학의 연쇄 법칙(chain rule) (섹션 5.2.2)을 사용하는 변수 변환(change-of-variable) 접근 방식**이다. 변수 변환 접근 방식은 변환으로 인한 결과 분포를 계산하려는 "레시피"를 제공하기 때문에 널리 사용된다. 우리는 단변량 확률 변수에 대한 기술을 설명하고, 다변량 확률 변수의 일반적인 경우에 대한 결과는 간략하게만 제공할 것이다. 이산 확률 변수의 변환은 직접적으로 이해할 수 있다. pmf $P(X=x)$ (섹션 6.2.1)를 갖는 이산 확률 변수 $X$와 가역 함수 $U(x)$가 있다고 가정하자. pmf $P(Y=y)$를 갖는 변환된 확률 변수 $Y:=U(X)$를 고려하자. 그러면

\begin{array}{rlr} P(Y=y) & =P(U(X)=y) & \text { transformation of interest } \ & =P\left(X=U^{-1}(y)\right) & \text { inverse } \end{array}

여기서 $x=U^{-1}(y)$임을 알 수 있다. 따라서 이산 확률 변수의 경우, **변환은 개별 사건을 직접적으로 변경한다 (확률은 적절하게 변환된다).** 모멘트 생성 함수(Moment generating functions)는 확률 변수의 변환을 연구하는 데에도 사용될 수 있다 (Casella and Berger, 2002, chapter 2). ### 6.7.1 Distribution Function Technique **분포 함수 기법(distribution function technique)**은 기본 원리로 돌아가 **누적 분포 함수(cdf)** $F_{X}(x)=P(X \leqslant x)$의 정의와 그 미분이 **확률 밀도 함수(pdf)** $f(x)$라는 사실을 이용한다 (Wasserman, 2004, chapter 2). 확률 변수 $X$와 함수 $U$에 대해, 우리는 $Y:=U(X)$인 확률 변수 $Y$의 pdf를 다음 단계로 찾는다: 1. **cdf 찾기**: $$ F_{Y}(y)=P(Y \leqslant y) $$ 2. **cdf $F_{Y}(y)$를 미분하여 pdf $f(y)$ 얻기**: $$ f(y)=\frac{\mathrm{d}}{\mathrm{~d} y} F_{Y}(y) $$ 또한, $U$에 의한 변환으로 인해 확률 변수의 **도메인(domain)**이 변경될 수 있다는 점을 염두에 두어야 한다. ## Example 6.16 $0 \leqslant x \leqslant 1$ 범위에서 확률 밀도 함수(pdf)가 다음과 같은 연속 확률 변수 $X$가 있다고 하자.

f(x)=3 x^{2} .

우리는 $Y=X^{2}$의 pdf를 찾는 데 관심이 있다. 함수 $f$는 $x$에 대한 증가 함수이므로, 결과적으로 $y$ 값은 구간 $[0,1]$에 속한다. 우리는 다음을 얻는다.

\begin{array}{rlr} F_{Y}(y) & =P(Y \leqslant y) & \text { cdf의 정의 } \ & =P\left(X^{2} \leqslant y\right) & \text { 관심 있는 변환 } \ & =P\left(X \leqslant y^{\frac{1}{2}}\right) & \text { 역함수 } \ & =F_{X}\left(y^{\frac{1}{2}}\right) & \text { cdf의 정의 } \ & =\int_{0}^{y^{\frac{1}{2}}} 3 t^{2} \mathrm{~d} t & \text { 정적분으로서의 cdf } \ & \left.=t^{3}\right]_{t=0}^{t=y^{\frac{1}{2}}} & \text { 적분 결과 } \ & =y^{\frac{3}{2}}, \quad 0 \leqslant y \leqslant 1 . & \end{array}

따라서 $Y$의 cdf는 다음과 같다.

F_{Y}(y)=y^{\frac{3}{2}}

$0 \leqslant y \leqslant 1$ 범위에서. pdf를 얻기 위해 cdf를 미분한다.

f(y)=\frac{\mathrm{d}}{\mathrm{~d} y} F_{Y}(y)=\frac{3}{2} y^{\frac{1}{2}}

$0 \leqslant y \leqslant 1$ 범위에서. 예제 6.16에서 우리는 엄격하게 단조 증가하는 함수를 고려했다. 역함수를 갖는 함수를 **전단사 함수(bijective functions)**라고 한다(섹션 2.7). 함수 $f(x)=3 x^{2}$. 이는 우리가 역함수를 계산할 수 있음을 의미한다. 일반적으로 우리는 관심 있는 함수 $y=U(x)$가 역함수 $x=U^{-1}(y)$를 가질 것을 요구한다. 확률 변수 $X$의 누적 분포 함수 $F_{X}(x)$를 고려하고 이를 변환 $U(x)$로 사용함으로써 유용한 결과를 얻을 수 있다. 이는 다음 정리로 이어진다. 정리 6.15. [Casella and Berger (2002)의 정리 2.1.10] $X$가 엄격하게 단조적인 누적 분포 함수 $F_{X}(x)$를 갖는 연속 확률 변수라고 하자. 그러면 다음과 같이 정의된 확률 변수 $Y$는

Y:=F_{X}(X)

**균등 분포(uniform distribution)**를 따른다. 정리 6.15는 **확률 적분 변환(probability integral transform)**으로 알려져 있으며, 균등 확률 변수에서 샘플링한 결과를 변환하여 분포에서 샘플링하는 알고리즘을 도출하는 데 사용된다(Bishop, 2006). 이 알고리즘은 먼저 균등 분포에서 샘플을 생성한 다음, 역 cdf(사용 가능한 경우)로 변환하여 원하는 분포에서 샘플을 얻는 방식으로 작동한다. 확률 적분 변환은 또한 샘플이 특정 분포에서 왔는지 여부를 가설 검정하는 데 사용된다(Lehmann and Romano, 2005). cdf의 출력이 균등 분포를 제공한다는 아이디어는 **코퓰라(copulas)**의 기초를 형성하기도 한다(Nelsen, 2006). ### 6.7.2 Change of Variables 섹션 6.7.1의 **분포 함수 기법(distribution function technique)**은 cdf의 정의와 역함수, 미분, 적분의 속성을 기반으로 **첫 번째 원칙(first principles)**으로부터 도출된다. 이 첫 번째 원칙으로부터의 논증은 두 가지 사실에 의존한다: 1. $Y$의 cdf를 $X$의 cdf인 표현으로 변환할 수 있다. 2. cdf를 미분하여 pdf를 얻을 수 있다. 정리 6.16의 더 일반적인 **변수 변환(change-of-variables)** 접근 방식을 이해하기 위해 단계별로 추론을 분석해 보자. **참고.** "변수 변환"이라는 이름은 어려운 적분을 만났을 때 적분 변수를 변경하는 아이디어에서 유래한다. 단변량 함수(univariate functions)의 경우, 우리는 적분의 치환 규칙(substitution rule)을 사용한다.

\int f(g(x)) g^{\prime}(x) \mathrm{d} x=\int f(u) \mathrm{d} u, \quad \text { where } \quad u=g(x)

이 규칙의 도출은 미적분학의 연쇄 법칙(chain rule of calculus) (5.32)과 미적분학의 기본 정리(fundamental theorem of calculus)를 두 번 적용하는 것에 기반한다. 미적분학의 기본 정리는 적분과 미분이 서로 "역함수" 관계라는 사실을 형식화한다. 이 규칙에 대한 직관적인 이해는 $u=g(x)$ 방정식에 대한 작은 변화(미분)를 (느슨하게) 생각함으로써 얻을 수 있다. 즉, $\Delta u=g^{\prime}(x) \Delta x$를 $u=g(x)$의 미분으로 간주하는 것이다. $u=g(x)$를 대입하면 (6.133)의 우변에 있는 적분 내부의 인수는 $f(g(x))$가 된다. $\mathrm{d} u$ 항이 $\mathrm{d} u \approx \Delta u=g^{\prime}(x) \Delta x$로 근사될 수 있고, $\mathrm{d} x \approx \Delta x$라고 가정하면 (6.133)을 얻는다. 단변량 확률 변수 $X$와 역함수 $U$를 고려해 보자. 이 함수는 또 다른 확률 변수 $Y=U(X)$를 제공한다. 확률 변수 $X$는 $x \in[a, b]$ 상태를 가진다고 가정한다. cdf의 정의에 따라 다음을 얻는다.

F_{Y}(y)=P(Y \leqslant y)

확률에서의 변수 변환은 미적분학의 변수 변환 방법에 의존한다 (Tandra, 2014). 우리는 확률 변수의 함수 $U$에 관심이 있다.

P(Y \leqslant y)=P(U(X) \leqslant y),

여기서 함수 $U$는 **가역적(invertible)**이라고 가정한다. 한 구간에서 가역적인 함수는 **단조 증가(strictly increasing)**하거나 **단조 감소(strictly decreasing)**한다. $U$가 단조 증가하는 경우, 그 역함수 $U^{-1}$도 단조 증가한다. $P(U(X) \leqslant y)$의 인수에 역함수 $U^{-1}$를 적용하면 다음을 얻는다.

P(U(X) \leqslant y)=P\left(U^{-1}(U(X)) \leqslant U^{-1}(y)\right)=P\left(X \leqslant U^{-1}(y)\right) .

(6.136)의 가장 오른쪽 항은 $X$의 cdf 표현이다. pdf 측면에서 cdf의 정의를 상기해 보자.

P\left(X \leqslant U^{-1}(y)\right)=\int_{a}^{U^{-1}(y)} f(x) \mathrm{d} x

이제 $x$ 측면에서 $Y$의 cdf 표현을 얻었다.

F_{Y}(y)=\int_{a}^{U^{-1}(y)} f(x) \mathrm{d} x

pdf를 얻기 위해 (6.138)을 $y$에 대해 미분한다.

f(y)=\frac{\mathrm{d}}{\mathrm{~d} y} F_{y}(y)=\frac{\mathrm{d}}{\mathrm{d} y} \int_{a}^{U^{-1}(y)} f(x) \mathrm{d} x

우변의 적분은 $x$에 대한 것이지만, 우리는 $y$에 대해 미분하고 있으므로 $y$에 대한 적분이 필요하다. 특히, (6.133)을 사용하여 다음 치환을 얻는다.

\int f\left(U^{-1}(y)\right) U^{-1^{\prime}}(y) \mathrm{d} y=\int f(x) \mathrm{d} x \quad \text { where } \quad x=U^{-1}(y) .

$$(6.139)의 우변에 (6.140)을 사용하면 다음을 얻는다.$$

f(y)=\frac{\mathrm{d}}{\mathrm{d} y} \int_{a}^{U^{-1}(y)} f_{x}\left(U^{-1}(y)\right) U^{-1^{\prime}}(y) \mathrm{d} y

미분은 선형 연산자이며, $f_{x}\left(U^{-1}(y)\right)$가 $y$가 아닌 $x$의 함수임을 상기시키기 위해 아래 첨자 $x$를 사용한다. 미적분학의 기본 정리를 다시 적용하면 다음을 얻는다.

f(y)=f_{x}\left(U^{-1}(y)\right) \cdot\left(\frac{\mathrm{d}}{\mathrm{d} y} U^{-1}(y)\right) .

우리는 $U$가 단조 증가 함수라고 가정했다. 감소 함수의 경우, 동일한 도출 과정을 따르면 음수 부호가 나타난다. 증가하는 $U$와 감소하는 $U$ 모두에 대해 동일한 표현을 갖도록 미분의 **절대값(absolute value)**을 도입한다.

f(y)=f_{x}\left(U^{-1}(y)\right) \cdot\left|\frac{\mathrm{d}}{\mathrm{d} y} U^{-1}(y)\right| .

이를 **변수 변환 기법(change-of-variable technique)**이라고 한다. (6.143)의 항 $\left|\frac{\mathrm{d}}{\mathrm{d} y} U^{-1}(y)\right|$는 $U$를 적용할 때 단위 부피가 얼마나 변하는지를 측정한다 (섹션 5.3의 **야코비안(Jacobian)** 정의도 참조). **참고.** (6.125b)의 이산 사례와 비교하여, 우리는 추가적인 인자 $\left|\frac{\mathrm{d}}{\mathrm{d} y} U^{-1}(y)\right|$를 갖는다. 연속 사례는 $P(Y=y)=0$이 모든 $y$에 대해 성립하므로 더 많은 주의가 필요하다. 확률 밀도 함수 $f(y)$는 $y$를 포함하는 사건의 확률로 설명되지 않는다. 이 섹션에서 지금까지 우리는 단변량 변수 변환을 연구했다. 다변량 확률 변수의 경우도 유사하지만, 절대값을 다변량 함수에 사용할 수 없다는 사실 때문에 복잡해진다. 대신 **야코비안 행렬(Jacobian matrix)**의 **행렬식(determinant)**을 사용한다. (5.58)에서 야코비안은 편미분 행렬이며, 0이 아닌 행렬식의 존재는 야코비안을 역변환할 수 있음을 보여준다는 것을 상기해 보자. 섹션 4.1의 논의에서 행렬식이 발생하는 이유는 우리의 미분(부피의 정육면체)이 야코비안에 의해 평행육면체로 변환되기 때문이라는 것을 상기해 보자. 다음 정리에서 앞선 논의를 요약해 보자. 이 정리는 다변량 변수 변환에 대한 방법을 제공한다. **정리 6.16.** [Billingsley (1995)의 정리 17.2] $f(\boldsymbol{x})$를 다변량 연속 확률 변수 $X$의 확률 밀도 값이라고 하자. 벡터 값 함수 $\boldsymbol{y}=U(\boldsymbol{x})$가 $\boldsymbol{x}$의 도메인 내의 모든 값에 대해 미분 가능하고 가역적이라면, 해당 $\boldsymbol{y}$ 값에 대해 $Y=U(X)$의 확률 밀도는 다음으로 주어진다.

f(\boldsymbol{y})=f_{\boldsymbol{x}}\left(U^{-1}(\boldsymbol{y})\right) \cdot\left|\operatorname{det}\left(\frac{\partial}{\partial \boldsymbol{y}} U^{-1}(\boldsymbol{y})\right)\right| .

이 정리는 언뜻 보기에 위협적으로 보이지만, 핵심은 다변량 확률 변수의 변수 변환이 단변량 변수 변환의 절차를 따른다는 것이다. 먼저 역변환을 계산하고 이를 $\boldsymbol{x}$의 밀도에 대입해야 한다. 그런 다음 야코비안의 행렬식을 계산하고 결과를 곱한다. 다음 예시는 이변량 확률 변수의 경우를 보여준다. ## Example 6.17 상태가 $\boldsymbol{x}=\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right]$이고 확률 밀도 함수가 다음과 같은 이변량 확률 변수 $X$를 고려해 보자.

f\left(\left[\begin{array}{l} x_{1} \ x_{2} \end{array}\right]\right)=\frac{1}{2 \pi} \exp \left(-\frac{1}{2}\left[\begin{array}{l} x_{1} \ x_{2} \end{array}\right]^{\top}\left[\begin{array}{l} x_{1} \ x_{2} \end{array}\right]\right)

**변수 변환 기법 (change-of-variable technique)** 우리는 Theorem 6.16의 **변수 변환 기법**을 사용하여 확률 변수의 선형 변환(Section 2.7)의 효과를 도출한다. 다음과 같이 정의된 행렬 $\boldsymbol{A} \in \mathbb{R}^{2 \times 2}$를 고려해 보자.

\boldsymbol{A}=\left[\begin{array}{ll} a & b \ c & d \end{array}\right]

우리는 상태가 $\boldsymbol{y}=\boldsymbol{A} \boldsymbol{x}$인 변환된 이변량 확률 변수 $Y$의 확률 밀도 함수를 찾는 데 관심이 있다. 변수 변환을 위해서는 $\boldsymbol{y}$의 함수로서 $\boldsymbol{x}$의 역변환이 필요하다는 것을 상기하자. 선형 변환을 고려하므로, 역변환은 행렬 역행렬(Section 2.2.2 참조)에 의해 주어진다. $2 \times 2$ 행렬의 경우, 다음과 같이 공식을 명시적으로 작성할 수 있다.

\left[\begin{array}{l} x_{1} \ x_{2} \end{array}\right]=\boldsymbol{A}^{-1}\left[\begin{array}{l} y_{1} \ y_{2} \end{array}\right]=\frac{1}{a d-b c}\left[\begin{array}{cc} d & -b \ -c & a \end{array}\right]\left[\begin{array}{l} y_{1} \ y_{2} \end{array}\right] .

$a d-b c$는 $\boldsymbol{A}$의 **행렬식 (determinant)**(Section 4.1)임을 알 수 있다. 해당 확률 밀도 함수는 다음과 같이 주어진다.

f(\boldsymbol{x})=f\left(\boldsymbol{A}^{-1} \boldsymbol{y}\right)=\frac{1}{2 \pi} \exp \left(-\frac{1}{2} \boldsymbol{y}^{\top} \boldsymbol{A}^{-\top} \boldsymbol{A}^{-1} \boldsymbol{y}\right)

$$행렬과 벡터의 곱을 벡터에 대해 편미분하면 그 행렬 자체가 된다(Section 5.5). 따라서$$

\frac{\partial}{\partial \boldsymbol{y}} \boldsymbol{A}^{-1} \boldsymbol{y}=\boldsymbol{A}^{-1}

$$Section 4.1에서 역행렬의 행렬식은 행렬식의 역수라는 것을 상기하면, **Jacobian 행렬**의 행렬식은 다음과 같다.$$

\operatorname{det}\left(\frac{\partial}{\partial \boldsymbol{y}} \boldsymbol{A}^{-1} \boldsymbol{y}\right)=\frac{1}{a d-b c} .

$$이제 (6.148)에 (6.150)을 곱하여 Theorem 6.16의 **변수 변환 공식**을 적용할 수 있으며, 이는 다음을 산출한다.$$

\begin{aligned} f(\boldsymbol{y}) & =f(\boldsymbol{x})\left|\operatorname{det}\left(\frac{\partial}{\partial \boldsymbol{y}} \boldsymbol{A}^{-1} \boldsymbol{y}\right)\right| \ & =\frac{1}{2 \pi} \exp \left(-\frac{1}{2} \boldsymbol{y}^{\top} \boldsymbol{A}^{-\top} \boldsymbol{A}^{-1} \boldsymbol{y}\right)|a d-b c|^{-1} \end{aligned}

Example 6.17은 이변량 확률 변수를 기반으로 하여 행렬 역행렬을 쉽게 계산할 수 있지만, 앞의 관계는 더 높은 차원에서도 유효하다. 참고. Section 6.5에서 (6.148)의 밀도 $f(\boldsymbol{x})$는 사실 **표준 가우시안 분포 (standard Gaussian distribution)**이며, 변환된 밀도 $f(\boldsymbol{y})$는 공분산 $\boldsymbol{\Sigma}=\boldsymbol{A} \boldsymbol{A}^{\top}$를 갖는 **이변량 가우시안 (bivariate Gaussian)**임을 보았다. 우리는 이 장의 아이디어를 사용하여 Section 8.4에서 **확률적 모델링 (probabilistic modeling)**을 설명하고, Section 8.5에서 **그래픽 언어 (graphical language)**를 소개할 것이다. Chapter 9와 11에서 이러한 아이디어의 직접적인 머신러닝 응용을 볼 것이다. ### 6.8 Further Reading 이 장은 때때로 다소 간결하게 서술되어 있다. Grinstead와 Snell (1997), Walpole 등 (2011)은 독학에 적합한 보다 편안한 설명을 제공한다. 확률의 철학적 측면에 관심 있는 독자는 Hacking (2001)을 고려할 수 있으며, 소프트웨어 공학과 더 관련 있는 접근 방식은 Downey (2014)에 제시되어 있다. **exponential families**에 대한 개요는 Barndorff-Nielsen (2014)에서 찾을 수 있다. 확률 분포를 사용하여 머신러닝 task를 모델링하는 방법에 대해서는 8장에서 더 자세히 다룰 것이다. 아이러니하게도, 최근 **neural networks**에 대한 관심이 급증하면서 확률 모델에 대한 더 폭넓은 인식이 생겨났다. 예를 들어, **normalizing flows** (Jimenez Rezende와 Mohamed, 2015)의 아이디어는 **random variables**를 변환하기 위한 **change of variables**에 의존한다. **neural networks**에 적용된 **variational inference** 방법에 대한 개요는 Goodfellow 등 (2016)의 책 16장부터 20장에 설명되어 있다. 우리는 **measure theoretic questions** (Billingsley, 1995; Pollard, 2002)을 피하고, 실수와 실수에 대한 집합을 정의하는 방법, 그리고 그 적절한 발생 빈도를 구성 없이 가정함으로써 **continuous random variables**의 어려움 중 상당 부분을 회피했다. 이러한 세부 사항은 예를 들어, **continuous random variables** $x, y$에 대한 **conditional probability** $p(y \mid x)$를 명시하는 데 중요하다 (Proschan과 Presnell, 1998). 게으른 표기법은 우리가 $X=x$ (측도 0인 집합)를 명시하고자 한다는 사실을 숨긴다. 또한, 우리는 $y$의 **probability density function**에 관심이 있다. 더 정확한 표기법은 $\mathbb{E}_{y}[f(y) \mid \sigma(x)]$라고 해야 할 것이다. 여기서 우리는 $x$의 $\sigma$-algebra에 조건화된 **test function** $f$의 $y$에 대한 기댓값을 취한다. 확률 이론의 세부 사항에 관심 있는 기술적인 독자들은 많은 선택지가 있다 (Jaynes, 2003; MacKay, 2003; Jacod과 Protter, 2004; Grimmett과 Welsh, 2014). 여기에는 매우 기술적인 논의도 포함된다 (Shiryayev, 1984; Lehmann과 Casella, 1998; Dudley, 2002; Bickel과 Doksum, 2006; Çinlar, 2011). 확률에 접근하는 또 다른 방법은 기댓값의 개념에서 시작하여 **probability space**의 필요한 속성을 도출하기 위해 "거꾸로 작업하는" 것이다 (Whittle, 2000). 머신러닝이 점점 더 복잡한 유형의 데이터에 대해 더 복잡한 분포를 모델링할 수 있게 됨에 따라, 확률적 머신러닝 모델 개발자는 이러한 더 기술적인 측면을 이해해야 할 것이다. 확률적 모델링에 중점을 둔 머신러닝 서적에는 MacKay (2003); Bishop (2006); Rasmussen과 Williams (2006); Barber (2012); Murphy (2012)의 책들이 포함된다. ## Exercises 6.1 두 개의 이산 확률 변수 $X$와 $Y$의 이변량 분포 $p(x, y)$를 고려해 보자. | $Y$ | $y_{1}$ | 0.01 | 0.02 | 0.03 | 0.1 | 0.1 | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | | $y_{2}$ | 0.05 | 0.1 | 0.05 | 0.07 | 0.2 | | | $y_{3}$ | 0.1 | 0.05 | 0.03 | 0.05 | 0.04 | | | | | | | | | | | $X$ | | | | | | ## Compute: a. 주변 분포(marginal distributions) $p(x)$ 및 $p(y)$. b. 조건부 분포(conditional distributions) $p\left(x \mid Y=y_{1}\right)$ 및 $p\left(y \mid X=x_{3}\right)$. 6.2 두 Gaussian 분포의 혼합(Figure 6.4 참조)을 고려한다.

0.4 \mathcal{N}\left(\left[\begin{array}{c} 10 \ 2 \end{array}\right],\left[\begin{array}{ll} 1 & 0 \ 0 & 1 \end{array}\right]\right)+0.6 \mathcal{N}\left(\left[\begin{array}{l} 0 \ 0 \end{array}\right],\left[\begin{array}{ll} 8.4 & 2.0 \ 2.0 & 1.7 \end{array}\right]\right)

a. 각 차원에 대한 주변 분포를 계산한다. b. 각 주변 분포에 대한 평균(mean), 최빈값(mode), 중앙값(median)을 계산한다. c. 2차원 분포에 대한 평균(mean)과 최빈값(mode)을 계산한다. 6.3 때로는 컴파일되고 때로는 컴파일되지 않는(코드는 변경되지 않음) 컴퓨터 프로그램을 작성했다. 컴파일러의 명백한 확률성(성공 대 실패) $x$를 매개변수 $\mu$를 갖는 Bernoulli 분포를 사용하여 모델링하기로 결정한다.

p(x \mid \mu)=\mu^{x}(1-\mu)^{1-x}, \quad x \in{0,1}

Bernoulli likelihood에 대한 **켤레 사전 분포(conjugate prior)**를 선택하고 사후 분포(posterior distribution) $p\left(\mu \mid x_{1}, \ldots, x_{N}\right)$를 계산한다. 6.4 두 개의 가방이 있다. 첫 번째 가방에는 망고 4개와 사과 2개가 들어 있고, 두 번째 가방에는 망고 4개와 사과 4개가 들어 있다. 또한 앞면이 나올 확률이 0.6이고 뒷면이 나올 확률이 0.4인 **편향된 동전(biased coin)**이 있다. 동전이 앞면이 나오면 가방 1에서 무작위로 과일을 선택하고, 그렇지 않으면 가방 2에서 무작위로 과일을 선택한다. 친구가 동전을 던지고(결과를 볼 수 없음), 해당 가방에서 무작위로 과일을 선택하여 망고를 건네준다. 망고가 가방 2에서 선택되었을 확률은 얼마인가? 힌트: **Bayes' theorem**을 사용한다. 6.5 시계열 모델을 고려한다.

\begin{aligned} \boldsymbol{x}{t+1} & =\boldsymbol{A} \boldsymbol{x}{t}+\boldsymbol{w}, & & \boldsymbol{w} \sim \mathcal{N}(\mathbf{0}, \boldsymbol{Q}) \ \boldsymbol{y}{t} & =\boldsymbol{C} \boldsymbol{x}{t}+\boldsymbol{v}, & & \boldsymbol{v} \sim \mathcal{N}(\mathbf{0}, \boldsymbol{R}), \end{aligned}

여기서 $\boldsymbol{w}, \boldsymbol{v}$는 **i.i.d. Gaussian noise** 변수이다. 또한 $p\left(\boldsymbol{x}_{0}\right)= \mathcal{N}\left(\boldsymbol{\mu}_{0}, \boldsymbol{\Sigma}_{0}\right)$라고 가정한다. a. $p\left(\boldsymbol{x}_{0}, \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{T}\right)$의 형태는 무엇인가? 답을 정당화한다(결합 분포를 명시적으로 계산할 필요는 없다). b. $p\left(\boldsymbol{x}_{t} \mid \boldsymbol{y}_{1}, \ldots, \boldsymbol{y}_{t}\right)=\mathcal{N}\left(\boldsymbol{\mu}_{t}, \boldsymbol{\Sigma}_{t}\right)$라고 가정한다. 1. $p\left(\boldsymbol{x}_{t+1} \mid \boldsymbol{y}_{1}, \ldots, \boldsymbol{y}_{t}\right)$를 계산한다. 2. $p\left(\boldsymbol{x}_{t+1}, \boldsymbol{y}_{t+1} \mid \boldsymbol{y}_{1}, \ldots, \boldsymbol{y}_{t}\right)$를 계산한다. 3. 시간 $t+1$에 값 $\boldsymbol{y}_{t+1}=\hat{\boldsymbol{y}}$를 관측한다. 조건부 분포 $p\left(\boldsymbol{x}_{t+1} \mid \boldsymbol{y}_{1}, \ldots, \boldsymbol{y}_{t+1}\right)$를 계산한다. 6.6 분산의 표준 정의와 분산에 대한 **raw-score 표현**을 연결하는 (6.44)의 관계를 증명한다. 6.7 데이터셋의 예시 간의 쌍별 차이와 분산에 대한 **raw-score 표현**을 연결하는 (6.45)의 관계를 증명한다. 6.8 Bernoulli 분포를 (6.107)에 있는 **지수족(exponential family)**의 **자연 매개변수(natural parameter)** 형태로 표현한다. 6.9 Binomial 분포를 지수족 분포로 표현한다. 또한 Beta 분포를 지수족 분포로 표현한다. Beta 분포와 Binomial 분포의 곱도 지수족의 구성원임을 보인다. 6.10 섹션 6.5.2의 관계를 두 가지 방법으로 도출한다. a. **제곱 완성(completing the square)**을 통해 b. Gaussian을 지수족 형태로 표현하여 두 Gaussian $\mathcal{N}(\boldsymbol{x} \mid \boldsymbol{a}, \boldsymbol{A}) \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{b}, \boldsymbol{B})$의 곱은 비정규화된 Gaussian 분포 $c \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{c}, \boldsymbol{C})$이며, 여기서

\begin{aligned} \boldsymbol{C} & =\left(\boldsymbol{A}^{-1}+\boldsymbol{B}^{-1}\right)^{-1} \ \boldsymbol{c} & =\boldsymbol{C}\left(\boldsymbol{A}^{-1} \boldsymbol{a}+\boldsymbol{B}^{-1} \boldsymbol{b}\right) \ c & =(2 \pi)^{-\frac{D}{2}}|\boldsymbol{A}+\boldsymbol{B}|^{-\frac{1}{2}} \exp \left(-\frac{1}{2}(\boldsymbol{a}-\boldsymbol{b})^{\top}(\boldsymbol{A}+\boldsymbol{B})^{-1}(\boldsymbol{a}-\boldsymbol{b})\right) . \end{aligned}

정규화 상수 $c$ 자체는 "팽창된(inflated)" 공분산 행렬 $\boldsymbol{A}+\boldsymbol{B}$를 갖는 $\boldsymbol{a}$ 또는 $\boldsymbol{b}$에 대한 (정규화된) Gaussian 분포로 간주될 수 있다. 즉, $c=\mathcal{N}(\boldsymbol{a} \mid \boldsymbol{b}, \boldsymbol{A}+\boldsymbol{B})=\mathcal{N}(\boldsymbol{b} \mid \boldsymbol{a}, \boldsymbol{A}+\boldsymbol{B})$이다. 6.11 **반복 기대값(Iterated Expectations)**. 결합 분포 $p(x, y)$를 갖는 두 확률 변수 $x, y$를 고려한다. 다음을 보인다.

\mathbb{E}{X}[x]=\mathbb{E}{Y}\left[\mathbb{E}_{X}[x \mid y]\right]

여기서 $\mathbb{E}_{X}[x \mid y]$는 조건부 분포 $p(x \mid y)$ 하에서 $x$의 기대값을 나타낸다. 6.12 **Gaussian 확률 변수의 조작(Manipulation of Gaussian Random Variables)**. Gaussian 확률 변수 $\boldsymbol{x} \sim \mathcal{N}\left(\boldsymbol{x} \mid \boldsymbol{\mu}_{x}, \boldsymbol{\Sigma}_{x}\right)$를 고려한다. 여기서 $\boldsymbol{x} \in \mathbb{R}^{D}$이다. 또한 다음이 성립한다.

y=A x+b+w

여기서 $\boldsymbol{y} \in \mathbb{R}^{E}, \boldsymbol{A} \in \mathbb{R}^{E \times D}, \boldsymbol{b} \in \mathbb{R}^{E}$이고, $\boldsymbol{w} \sim \mathcal{N}(\boldsymbol{w} \mid \mathbf{0}, \boldsymbol{Q})$는 독립적인 Gaussian noise이다. "독립적"이라는 것은 $\boldsymbol{x}$와 $\boldsymbol{w}$가 독립적인 확률 변수이고 $\boldsymbol{Q}$가 대각 행렬임을 의미한다. a. likelihood $p(\boldsymbol{y} \mid \boldsymbol{x})$를 작성한다. b. 분포 $p(\boldsymbol{y})=\int p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{x}) d \boldsymbol{x}$는 Gaussian이다. 평균 $\boldsymbol{\mu}_{y}$와 공분산 $\boldsymbol{\Sigma}_{y}$를 계산한다. 결과를 자세히 도출한다. c. 확률 변수 $\boldsymbol{y}$는 측정 매핑에 따라 변환된다.

z=C y+v

여기서 $\boldsymbol{z} \in \mathbb{R}^{F}, \boldsymbol{C} \in \mathbb{R}^{F \times E}$이고, $\boldsymbol{v} \sim \mathcal{N}(\boldsymbol{v} \mid \mathbf{0}, \boldsymbol{R})$는 독립적인 Gaussian (측정) noise이다. * $p(\boldsymbol{z} \mid \boldsymbol{y})$를 작성한다. * $p(\boldsymbol{z})$를 계산한다. 즉, 평균 $\boldsymbol{\mu}_{z}$와 공분산 $\boldsymbol{\Sigma}_{z}$를 계산한다. 결과를 자세히 도출한다. d. 이제 값 $\hat{\boldsymbol{y}}$가 측정된다. 사후 분포 $p(\boldsymbol{x} \mid \hat{\boldsymbol{y}})$를 계산한다. 해법 힌트: 이 사후 분포도 Gaussian이므로, 평균과 공분산 행렬만 결정하면 된다. 먼저 결합 Gaussian $p(\boldsymbol{x}, \boldsymbol{y})$를 명시적으로 계산하는 것부터 시작한다. 이를 위해서는 교차 공분산(cross-covariances) $\operatorname{Cov}_{\boldsymbol{x}, \boldsymbol{y}}[\boldsymbol{x}, \boldsymbol{y}]$ 및 $\operatorname{Cov}_{\boldsymbol{y}, \boldsymbol{x}}[\boldsymbol{y}, \boldsymbol{x}]$도 계산해야 한다. 그런 다음 Gaussian 조건화 규칙을 적용한다. ### 6.13 Probability Integral Transformation 연속 확률 변수 $X$가 cdf $F_{X}(x)$를 가질 때, 확률 변수 $Y:=F_{X}(X)$가 균등 분포를 따름을 보여라 (정리 6.15).